35. Алгоритм нахождения кратчайшего расстояния от источника до всех верши в общем случае – алгоритм Форда-Беллмана. Сложность алгоритма

__Кратчайшим путем между двумя вершинами называется путь имеющий минимальную дину.

__Кратчайшим расстоянием между двумя вершинами называется длина кратчайшего пути.

__Данные: Ориентированный граф <V, E> с  n вершинами с выделенным источником s Î V, матрица дуг A[u, v], u, v Î V (граф не содержит контуров отрицательной длины).

__Результаты: Расстояния от источника до всех вершин графа: D[v]=d(s, v), vÎV.

__В каждой итерации (верхний цикл) производится новая оценка расстояния для всех вершин v_i (средний цикл) кроме источника.

__Оценка расстояния для каждой вершины v_i, происходит путем сравнения расстояния через все вершины u_i существующие в этом графе, кроме источника (внутренний цикл): NО = D[v] и D[u]+A[u,v]

___В наихудшем случае, за каждую итерацию найденные минимальные пути включают 1 промежуточную вершину. Кратчайший путь между двумя вершинами в графе с n вершинами может содержать n-2 промежуточные вершины. Тогда в наихудшем случае потребуется n-2 итерации.

СЛОЖНОСТЬ АЛГОРИТМА:

__Очевидно, что временная сложность алгоритма есть O(n³). Три вложенных друг в друга цикла.

___Можно, закончить вычисления, когда выполнение очередной итерации не вызывает изменения ни одной из переменных D[v], v Î V. Это может наступить для k < n – 2, однако такая модификация алгоритма не изменяет существенным образом его сложности.

___Для редких графов (m << n²) удобнее представлять граф списками предшествующих вершин ПРЕДШ[v], v Î V. Заменяя строку 5 на

for u Î ПРЕДШ[v] do D [v] := min(D[v], D[u] + A [u, v]),

получаем алгоритм со сложностью O(nm).

36. Алгоритм Дейкстры — алгоритм нахождения кратчайшего расстояния от источника до всех верши в случае неотрицательных весов. Сложность алгоритма.

Данные: орграф <V, E> с n вершинами с выделенным источником s Î V, матрица весов A[u, v], u, v Î V (без отрицательных весов).

Результат: определены расстояния от источника до всех вершин графа: , .

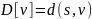Сложность алгоритма — .

Алгоритм:

• Находится минимальное расстояние от источника до какой-либо вершины.

• Найденное минимальное расстояние для этой вершины больше не изменяется.

• Вершина с минимальным расстоянием исключается из множества вершин, для которых ищут минимальное расстояние.

• Расстояние до этой вершины используется для оценки кратчайших расстояний до других вершин.

• Процесс повторяется, пока для каждой вершины не будет найдено минимальное расстояние.

37. Лемма о перенумерации вершин. Алгоритм перенумерации вершин графа.

Лемма. В произвольном бесконтурном графе вершины можно перенумеровать так, что каждая дуга будет иметь вид 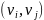, где .

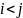Данные: ориентированный бесконтурный граф <V, E>, определяемый списками смежности ЗАПИСЬ [v], v Î V.

Результаты: Определен номер NR[v] для каждой вершины v Î V такой, что для произвольной дуги áu, vñ Î E выполняется нер-во NR[u] < NR[v].

NUM – номер последней пронумерованной вершины.

ЧЗАХ [v] – массив с числом дуг, вход. в каждую вершину.

CTEK – вершины, в которые не заходит ни одна дуга.

Сложность — О(m), т. к. каждая дуга анализир. 1 раз.

Алгоритм:

• Алгоритм основывается на том, что в произвольном (непустом) бесконтурном графе существует вершина, в которую не заходит ни одна дуга. Такие вершины накапливаются в стеке.

• В строке 10 выбирается верхний элемент стека u и этой вершине присваивается самый маленький из еще неиспользованных номеров. Т.е. все дуги, выходящие из этой вершины, ведут к вершине с большими номерами.

• Затем вершина u вместе с выходящими из нее дугами удаляется из графа. Это приводит к уменьшению на единицу числа дуг, заходящих в каждую вершину v и выходящую из u.

• Если для какой-нибудь вершины v число заходящих дуг сводится к нулю, то v помещается в стек.

• Опустошение стека, вызывающее окончание выполнения алгоритма (цикл 9), наступает не раньше, чем после присвоения номеров всем вершинам графа.

Begin

for v Î V do ЧЗАХ [v] := 0; ЧЗАХ [v] - число дуг, заходящих в v

for u Î V do

for v Î ЗАПИСЬ [u] do ЧЗАХ [v] := ЧЗАХ [v] + 1; // подсчет дуг в вершинах

СТЕК := Æ;

for v Î V do

if ЧЗАХ [v] = 0 then СТЕК Ü v; //если в v не заходят дуги, то она в СТЕК

num := 0; //обнуляем присваиваемый номер

while СТЕК ¹ Æ do

begin u Ü СТЕК; // достаем вершину из СТЕКа

num := num + 1; NR[u] := num; //присваиваем ей следующий номер

for v Î ЗАПИСЬ [u] do

begin ЧЗАХ [v] := ЧЗАХ [v] – 1; // уменьшаем на 1 число зах. в смеж. вер.

if ЧЗАХ [v] = 0 then СТЕК Ü v; //если в v нет дуг, вставляется в СТЕК

end

end

End