2. Поняття границі числової послідовності, її властивості. Теорема про границю монотонної числової послідовності. Теорема Больцано-Вейєрштраса

Нехай функція f (х) означена на множині N = {1,2,3,...,n...} всіх натуральних чисел. Така функція називається числовою послідовністю. Якщо позначити f (n) через у_n, то числову послідовність можна записати у вигляді {у_п}. При цьому у₁ називається першим членом послідовності, у₂ — другим і т. д., у_п — енним або загальним членом послідовності.

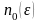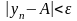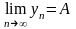Число А називається границею числової послідовності {y_п}, якщо для будь-якого числа > 0 існує натуральне число таке, що для всіх . Символічний запис: або .

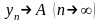Якщо послідовність {у_п} має границю А, то геометрично це означає, що всі члени цієї послідовності, починаючи з номера , потрапляють в інтервал 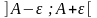, тобто в -окіл точки А. Що ж до членів у₁,у₂, . . ., , то про них в означенні границі нічого не говориться і, отже, вони можуть потрапляти в -окіл точки А, можуть знаходитись і поза цим околом. Числова послідовність, що має границю, називається збіжною, а та, що не має границі, — розбіжною.

Якщо {у_п} — задана послідовність і — яка-небудь зростаюча послідовність натуральних чисел, то послідовність 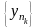називається підпослідовністю послідовності {у_п}. З означення границі послідовності випливає правильність твердження: якщо послідовність {у_п} має границю А, то й будь-яка її підпослідовність має ту саму границю А.

Справді, якщо число А є границею послідовності {у_п}, то для будь-якого числа в – окіл точки А потрапляють усі члени цієї послідовності, починаючи з деякого. Проте тоді в цей окіл потрапляють і всі члени підпослідовності починаючи з деякого. А це означає, що число А є границею підпослідовності .

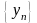Поняття часткової границі. Нехай дано числову послідовність . Точка А називається частковою границею послідовності , якщо в будь-який окіл цієї точки потрапляє нескінченна множина членів цієї послідовності. Наприклад, послідовність 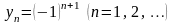має дві часткові границі 1 і -1. Справді, в будь-який окіл точки 1 (точки -1) потрапляють усі члени послідовності з непарними (з парними) індексами, а їх нескінченна множина. Інших часткових границь, відмінних від 1 і -1, ця послідовність не має.

Якщо послідовність збігається, то її границя одночасно є і її єдиною частковою границею. Обернене твердження, взагалі кажучи, неправильне. Послідовність

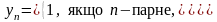
має єдину часткову границю, що дорівнює 1. Однак ця послідов­ність є розбіжною. Щоб послідовність, яка має єдину часткову границю, була збіжною, необхідно й достатньо, щоб вона була обмеженою. Це твердження сформулюємо нижче у вигляді теореми. Доведемо одне допоміжне твердження.

Теорема 1. (Больцано–Вейєрштрасса). Всяка обмежена числова послідовність має принаймні одну часткову границю.

Доведення. Оскільки послідовність {у_п}обмежена, то існує число М > 0 таке, що 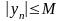для всіх п = 1, 2, .... Відрізку [-М; М] належать усі члени послідовності {у_п}. Цей відрізок точка О ділить на дві рівні частини. Принаймні одному з відрізків [-М; 0] і [0; М] належить нескінченна множина членів послідовності {у_п}. Цей відрізок позначимо [а₁, b₁] і точкою 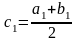поділимо його на дві рівні частини. Принаймні одному з відрізків [а₁; c₁] і [c₁; b₁]. належить нескінченна множина членів послідовності {у_п}. Той відрізок, якому належить нескінченна множина членів послідовності {у_п}, позначимо [а₂, b₂]. 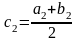Відрізок [а₂, b₂] точ­кою поділимо на дві рівні частини і той з двох від­різків [а₂; с₂] і [с₂; b₂], який містить нескінченну множину членів послідовності {у_п}, позначимо [а₃; b₃]. Цей процес продовжимо необмежено. В результаті дістанемо послідовність відрізків [а_n; b_n] (п= 1, 2, . . .) таку, що

1)

2. довжина відрізка , що дорівнює 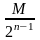прямує до нуля при ,

3. кожний відрізок (n=1, 2, . . .) містить нескінченну множину членів послідовності {у_п}.

З умов 1) і 2) за аксіомою Кантора випливає існування єдиної точки A, спільної для всіх відрізків (n=1, 2, . . .). Покаже­мо, що A є часткова границя послідовності {у_п}. Для цього візь­мемо довільний 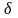-окіл точки A, тобто інтервал 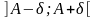. Оскільки 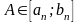для n=1, 2, . . ., а довжина відрізка [а_n; b_n] прямує до нуля при , то існує номер такий, що для всіх матиме місце включення

[a_n; b_n]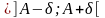 . (1)

Оскільки кожний відрізок містить нескінченну множину членів послідовності {у_п}, то звідси і з (1) випливає, що в -окіл точки A потрапляє нескінченна множина членів послідовності {у_п}. Це означає, що A є часткова границя послідовності {у_п}. Теорему доведено.

Нижня і верхня границі послідовності. Нехай дано обмежену послідовність {у_п}. Позначимо через F множину всіх її часткових границь. Ясно, що F– обмежена множина і внаслідок теореми Больцано — Вейєрштрасса вона містить принаймні одне число. За теоремою § 1.2 існують точна нижня і верхня межі множини F. Позначимо через

= inf F і = sup F.

Покажемо, що а і є частковими границями послідовності {у_п}, тобто і .

Візьмемо довільний -окіл точки . За властивістю супремуму для числа існує число таке, що 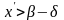. Візьмемо окіл 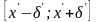точки х' настільки малий, щоб він цілком міс­тився в -околі точки . Оскільки х' є часткова границя послідов­ності {у_п}, то в -околі точки х' міститься нескінченна множина членів послідовності {у_п}. Ця нескінченна множина членів міститиметься і в -околі точки . Оскільки -окіл точки c було взято довільно, то є часткова границя послідовності {у_п}, тобто . Аналогічно можна показати, що й . Таким чином, є най­менша, а – найбільша часткові границі послідовності {у_п}. Най­більша (найменша) часткова границя послідовності {у_n} називається верхньою (нижньою) границею цієї послідовності і позначається

. Наприклад,

,

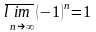Якщо послідовність {у_п} не обмежена знизу (зверху), то знайдеться підпослідовність 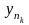така, що

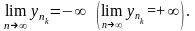
У цьому випадку нижньою (верхньою) границею послідовності за означенням природно вважати (+ ).

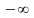Білет17