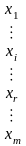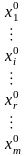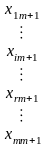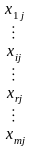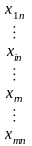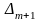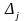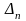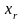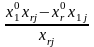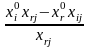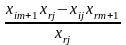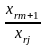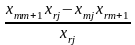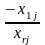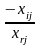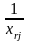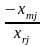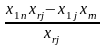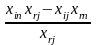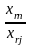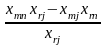- •Потужність множини. Зчисленні та незчисленні множини. Їх властивості.
- •2.Поняття моделі. Поняття інформаційної моделі. Поняття математичної моделі.
- •Приклади лінійних просторів
- •2.Алгоритм. Способи опису алгоритмів. Словесна та графічна форми подання алгоритмів.
- •1. Похідна функції однієї змінної, її геометричний та механічний зміст. Основні правила диференціювання.
- •3. Похідна складної функції.
- •1. Диференційовані функції однієї змінної, критерій диференційованості. Диференціал в точці, його геометричний зміст, застосування до наближених обчислень.
- •2. Програма. Поняття мови програмування. Поняття про середовище програмування
- •1. . Основні теореми диференціального числення. Теорема Лагранжа. Умови сталості та монотонності функції.
- •2. . Трансляція та її види: інтерпретація, компіляція. Їх особливості. Поняття системи програмування.
- •1. Екстремум функції. Необхідні умови екстремуму. Достатні умови екстремуму.
- •1. Максимум і мінімум функції в точці.
- •2. Основні принципи технології структурного програмування. Метод покрокової деталізації.
- •1. Структурне програмування
- •1.1. Принцип модульності
- •1. Первісна функція та неозначений інтеграл. Інтегрування підстановкою та частинами.
- •2. Основні принципи технології об’єктно-орієнтованого програмування. Поняття про об’єкт (клас).
- •1. Означений інтеграл. Необхідна умова інтегровності. Критерій інтегровності. Інтегровність неперервної функції.
- •Стандартні функції мови с
- •Аргументи функції
- •1. Квадровні фігури. Застосування означеного інтеграла до обчислення площ плоских фігур.
- •2. Алгоритми обробки масивів. Алгоритм послідовного пошуку. Пошук максимального (мінімального) елемента. Масиви даних
- •Одновимірні масиви (вектори)
- •1. Спрямлювані криві та їх довжини. Теорема Жордана. Обчислення довжини кривої за допомогою означеного інтеграла.
- •1. Застосування визначеного інтеграла до обчислення об’ємів тіл обертання та площ поверхонь обертання.
- •Задача про перевезення (транспортна задача)
- •1. Додатні числові ряди, властивості збіжних рядів, критерій збіжності. Теореми про порівняння рядів. Ознака Даламбера та інтегральна ознака Коші.
- •2. Метод штучного базису відшукання початкового базисного розв’язку злп. М-метод розв’язування злп.
- •1) Методи відшукання початкового базисного розв’язку
- •2) Описання м-методу розв’язування злп.
- •1Знакозмінні ряди. Ознака Лейбніца. Абсолютно і умовно збіжні ряди.
- •2. Двоїсті злп та їх властивості. Теореми двоїстості. Двоїстий симплекс-метод.
- •1. Функціональні послідовності і ряди. Збіжність, область збіжності. Рівномірна збіжність. Ознака Вейєрштраса.
- •2. Транспортна задача (тз). Властивості тз. Деякі методи відшукання початкового базисного розв’язку тз. Метод потенціалів розв’язування тз.
- •§2. Деякі властивості транспортної задачі.
- •§3. Базисні розв’язки транспортної задачі.
- •§4. Деякі методи відшукання базисного розв’язку транспортної задачі.
- •4.1. Метод північно-західного кута.
- •4.2. Метод мінімального елемента
- •§5. Метод потенціалів розв’язування транспортної задачі.
- •1. Метричні простори. Відкриті та замкнуті множини, їх властивості.
- •2. Потоки та мережі. Постановка задачі. Задача про найкоротший шлях. Метод Мінті. Задача про максимальний потік. Метод Форда-Фалкерсона.
- •3. Задача про максимальний потік. Метод Форда–Фалкерсона
- •1. Векторний добуток двох векторів, його властивості та застосування.
- •2. Поняття границі числової послідовності, її властивості. Теорема про границю монотонної числової послідовності. Теорема Больцано-Вейєрштраса
- •1.Еліпс, означення та канонічне рівняння. Дослідження форми еліпса за канонічним рівнянням.
- •Оптимальні чисті стратегії
- •§ 3. Оптимальні змішані стратегії
- •1. Означення детермінанта n-го порядку. Властивості детермінантів.
- •2. Правила суми і добутку. Розміщення, перестановки, комбінації (без повторень та з повтореннями).
- •2. Алгоритми обробки масивів. Сортування елементів масиву методом "бульбашки". Масиви даних
- •Одновимірні масиви (вектори)
- •1. Площини та прямі в просторі.
- •2. Теорема множення ймовірностей. Незалежність подій.
- •1. Поверхні другого порядку. Еліпсоїди, параболоїди, гіперболоїди, гіперболічний параболоїд.
- •Запишемо рівняння поверхні обертання, утвореної обертанням еліпса
- •Записуючи рівняння параболоїда обертання (6) у вигляді
- •На закінчення розглянемо
- •2. Формула повної ймовірності та формули Байєса.
- •1. Формула повної ймовірності та формули Байєса.
- •49.3. Матриця лінійного оператора. Приклади.
- •2. Опис рядків у мові програмування с. Операції над рядками, функції для обробки рядків Рядки
- •Функції обробки символів та рядків
- •Функції, що стосуються рядків, які розглядаються як послідовність байт.
- •Функції, що обробляють рядки
- •1. Множини та відношення. Основні види бінарних відношень. Розбиття множини на класи.
- •1. Лінійні диференціальні рівняння першого порядку та рівняння Бернуллі.
- •Рівняння в повних диференціалах
- •2. . Канонічні (нормальні) форми булевих функцій. Алгебра Жегалкіна.
- •1. Лінійні однорідні диференціальні рівняння n-го порядку із змінними коефіцієнтами. Фундаментальна система розв’язків. Детермінант Вронського. Загальний розв’язок.
- •2. Комбінаторні конфігурації. Біноміальна та поліноміальна теореми.
- •1. Розв’язування диференціальних рівнянь та їх систем.
- •2. Повнота і замкненість систем булевих функцій. Теорема (критерій) Поста.
- •1. Інтерполювання функцій многочленами Лагранжа.
- •Інтерполювання функцій многочленами Ньютона. Сплайни.
- •Скінченні різниці
- •Перша інтерполяційна формула Ньютона
- •Друга інтерполяційна формула Ньютона
- •1. Лінійна та нелінійна кореляція. Метод найменших квадратів. Побудова емпіричних формул.
- •2. . Опукле програмування. Функція Лагранжа. Теорема Куна-Таккера-1. Теорема Куна-Таккера-2. Задача опуклого квадратичного програмування. Квадратичний симплекс-метод. Задачі опуклого програмування.
- •Функція Лагранжа. Теореми Куна-Таккера.
Задача про перевезення (транспортна задача)
У
пунктах
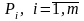 ,
виробляється деякий однорідний продукт,
причому у пункті
,
виробляється деякий однорідний продукт,
причому у пункті
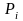 виробляється
одиниць продукції. У пункті
виробляється
одиниць продукції. У пункті
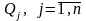 ,
споживається
,
споживається
 одиниць цього ж продукту. Припускається,
що
одиниць цього ж продукту. Припускається,
що
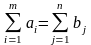
Нехай
 - собівартість перевезення одиниці
продукції з пункту
у пункт
- собівартість перевезення одиниці
продукції з пункту
у пункт
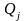 .
Необхідно знайти план перевезень
продукту таким чином, щоб задовольнити
потреби всіх споживачів, мінімізуючи
при цьому загальні транспортні витрати.
.
Необхідно знайти план перевезень
продукту таким чином, щоб задовольнити
потреби всіх споживачів, мінімізуючи
при цьому загальні транспортні витрати.
Нехай
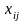 - невідома кількість продукції, що
планується для перевезення з
в
.
Тоді транспортна задача, яку прийнято
називати транспортною задачею лінійного
програмування (ТЗЛП), допомагає у
знаходженні плану перевезень
- невідома кількість продукції, що
планується для перевезення з
в
.
Тоді транспортна задача, яку прийнято
називати транспортною задачею лінійного
програмування (ТЗЛП), допомагає у
знаходженні плану перевезень
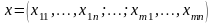 ,
що мінімізує загальні транспортні
витрати
,
що мінімізує загальні транспортні
витрати
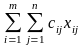
при обмеженнях
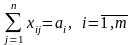 ,
,
 ,
,
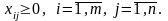
Зрозуміло, що отримана математична модель транспортної задачі є ЗЛП.
Також є такі практичні задачі, які зводяться до ЗЛП:
1. Задача про оптимальний розподіл ресурсів.
2. Задача про харчовий раціон (задача про дієту)
Загальна, стандартна та канонічна ЗЛП
Загальна ЗЛП формулюється таким чином:
знайти
вектор
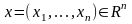 ,
що максимізує (мінімізує) лінійну функцію
,
що максимізує (мінімізує) лінійну функцію
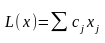 (2.1)
(2.1)
при обмеженнях
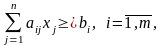 (2.2)
(2.2)
 , (2.3)
, (2.3)
Де
символ
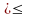 означає один із знаків
означає один із знаків
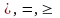 .
.
Вектор
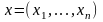 ,
що задовольняє обмеження (2.2), (2.3),
називається допустимим розв’язком
(вектором, точкою, пластом) ЗЛП (2.1) –
(2.3). Множина всіх допустимих розв’язків
ЗЛП називається допустимою областю
(множиною) ЗЛП і позначається літерою
,
що задовольняє обмеження (2.2), (2.3),
називається допустимим розв’язком
(вектором, точкою, пластом) ЗЛП (2.1) –
(2.3). Множина всіх допустимих розв’язків
ЗЛП називається допустимою областю
(множиною) ЗЛП і позначається літерою
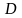 .
.
Канонічна форма ЗЛП має вигляд
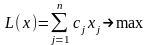
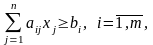
 .
.
Задача лінійного програмування з однотипними умовами формулюється таким чином:
Знайти
при обмеженнях
.
Канонічна форма ЗЛП та ЗЛП з однотипними умовами вважаються стандартними формами ЗЛП (СЗЛП).
Ознака оптимальності базисного розв’язку ЗЛП.
Будемо розглядати ЗЛП у канонічній формі:
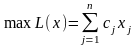 (3.1)
(3.1)
при обмеженнях
(3.2)
. (3.3)
Будемо позначати через
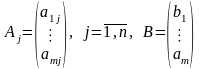 .
.
Вектори
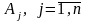 ,
ЗЛП (3.1) – (3.3) будемо називати векторами
умов, а вектор В
–
вектором обмежень цієї задачі.
,
ЗЛП (3.1) – (3.3) будемо називати векторами
умов, а вектор В
–
вектором обмежень цієї задачі.
Означення
3.1. Ненульовий допустимий розв’язок
ЗЛП (3.1) – (3.3) називається базисним, якщо
система векторів умов
 ,
що відповідають додатним координатам
,
що відповідають додатним координатам
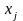 цього розв’язку, є лінійно незалежною.
цього розв’язку, є лінійно незалежною.
Означення 3.2. Базисний розв’язок ЗЛП (3.1) – (3.3) називається не виродженим, якщо він містить рівно т додатних компонент, та виродженим, якщо додатних компонент менше т.
У цьому випадку базисом, що порядкує розв'язок (3.5) є будь-яка система т лінійно незалежних векторів умов, що включає вектори А1, …,Аr.
Нехай
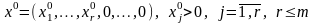 ,
- базисний розв'язок ЗЛП (3.1) – (3.3), а А1,
…,Аr
– відповідний йому базис. Система
рівнянь (3.2) еквівалентна такій системі
,
- базисний розв'язок ЗЛП (3.1) – (3.3), а А1,
…,Аr
– відповідний йому базис. Система
рівнянь (3.2) еквівалентна такій системі
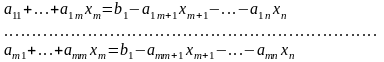 (3.6)
(3.6)
Остання система в свою чергу буде еквівалентною такій системі
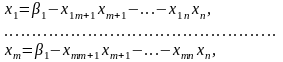 (3.7)
(3.7)
Підставивши (3.6) в (3.1) отримаємо запис ЗЛП (3.1) – (3.3) в такій еквівалентній формі
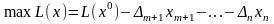 (3.8)
(3.8)
при обмеженнях
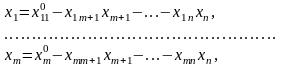 (3.9)
(3.9)
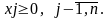
Інформацію про ЗЛП (3.1) - (3.3), записаному у еквівалентній формі (3.8) – (3.9), що відповідає базисному розв'язку х0, можна записати у вигляді такої симплекс-таблиці.
Базисні змінні |
Значення базисної змінної |
Небазисні змінні |
||||
хт+1 |
… |
|
… |
хп |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема
3.1.
(ознака оптимальності базисного розв'язку
ЗЛП). Якщо для деякого базисного розв'язку
х0
справджуються нерівності
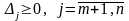 ,
то х0
– оптимальний розв'язок ЗЛП (3.1) – (3.3).
,
то х0
– оптимальний розв'язок ЗЛП (3.1) – (3.3).
Доведення. Нехай х = (х1,…,хп) довільний допустимий розв'язок ЗЛП (3.1) – (3.3) і, ЗЛП (3.8) – (3.9), яка еквівалентна задачі (3.1) – (3.3)
Оскільки
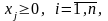 то з (3.8) та нерівності
,
отримаємо, що
то з (3.8) та нерівності
,
отримаємо, що
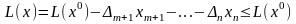
Що й доводить теорему.
Теорема
3.2.
(ознака необмеженості цільової функції
ЗЛП на допустимій множині). Якщо для
деякого базисного розв'язку х0
ЗОП (3.1) – (3.3) ((3.8) – (3.9)) існує хоча б одне
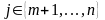 таке, що
таке, що
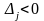 і
і
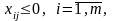 то цільова функція ЗЛП необмежена зверху
на допустимій множині, тобто
то цільова функція ЗЛП необмежена зверху
на допустимій множині, тобто
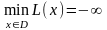 .
.
Алгоритм симплекс-методу розв'язання ЗЛП. Про скінченність алгоритму симплекс методу.
Нехай
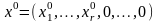 її базисний розв’язок. Якщо для цього
розв’язку
,
то згідно з теоремою 1 х0
є
оптимальним розв’язком цієї задачі.
Якщо ж для деякого
і
то згідно з теоремою 2 цільова функція
її базисний розв’язок. Якщо для цього
розв’язку
,
то згідно з теоремою 1 х0
є
оптимальним розв’язком цієї задачі.
Якщо ж для деякого
і
то згідно з теоремою 2 цільова функція
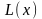 необмежена зверху на
і в цьому випадку задача вважається
розв’язаною, оскільки з’ясовано, що
оптимального розв’язку не існує і
необмежена зверху на
і в цьому випадку задача вважається
розв’язаною, оскільки з’ясовано, що
оптимального розв’язку не існує і
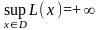 .
.
Нехай тепер для кожного , для якого , серед елементів є більші нуля.
Алгоритму симплекс-методу розв’язування ЗЛП (3.1)-(3.3) з допомогою переходу від одного базисного розв’язку до кращого базисного розв’язку (від однієї симплекс-таблиці до “кращої” симплекс-таблиці).
Нехай маємо базисний розв’язок
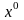 ЗЛП (3.1)-(3.3). Заповнюємо симплекс-таблицю
(3.11), що відповідає цьому базисному
розв’язку.
ЗЛП (3.1)-(3.3). Заповнюємо симплекс-таблицю
(3.11), що відповідає цьому базисному
розв’язку.Проглядаємо симплекс-різниці
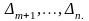 Якщо
Якщо
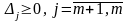 ,
то
є оптимальним розв’язком ЗЛП (3.1)-(3.3).
,
то
є оптимальним розв’язком ЗЛП (3.1)-(3.3).Якщо ні, то вибираємо найменшу симплекс-різницю . Тоді стовпець симплекс-таблиці, в якому знаходиться називаємо розв’язуючим стовпцем. Розв’язуючий стовпець виділяємо стрілочкою.
Для
відшукання розв’язуючого рядка знаходимо
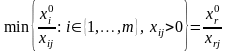 .
.
На
перетині розв’язуючих стовпця та рядка
стоїть розв’язуючий елемент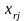 ,
який заключатимемо в кружечок.
,
який заключатимемо в кружечок.
5. Перехід до наступної симплекс-таблиці здійснюється, за таким правилом:
Базисні змінні |
Значення базисних змінних |
Небазисні змінні |
||||
хm+1 |
|
|
|
xn |
||
х1
xi
xj
xm |
|
|
|
|
|
|
|
L(x0) |
|
|
|
|
|
Переходимо до кроку №1.
Про скінченність симплекс методу.
ЗЛП (3.1)-(3.3) будемо називати не виродженою, якщо не виродженими є всі її базисні розв’язки.
Розглянемо
спочатку не вироджену ЗЛП (3.1)-(3.3). Як
зазначалось у §4 в цьому випадку крок
симплекс-методу приведе від базисного
розв’язку
до базисного розв’язку
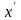 такого, що
такого, що
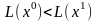 .
Звідси випливає, що
.
Звідси випливає, що
 . Аналогічно наступний крок дасть
базисний розв’язок
. Аналогічно наступний крок дасть
базисний розв’язок
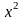 такий, що
такий, що
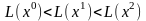 і т.д. Отже, у випадку невиродженості
ЗЛП (3.1)-(3.3) базисні розв’язки, отримувані
в результаті застосування симплекс-методу,
попарно різні. Оскільки базисних
розв’язків ЗЛП (3.1)-(3.3) має скінчену
кількість, то процес застосування до
її розв’язування симплекс-методу є
скінченим. Це означає, що через скінчену
кількість кроків буде знайдено оптимальний
розв’язок ЗЛП, або виявлено, що
і т.д. Отже, у випадку невиродженості
ЗЛП (3.1)-(3.3) базисні розв’язки, отримувані
в результаті застосування симплекс-методу,
попарно різні. Оскільки базисних
розв’язків ЗЛП (3.1)-(3.3) має скінчену
кількість, то процес застосування до
її розв’язування симплекс-методу є
скінченим. Це означає, що через скінчену
кількість кроків буде знайдено оптимальний
розв’язок ЗЛП, або виявлено, що
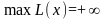 .
.
У
випадку вродженості ЗЛП (3.1)-(3.3)
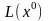 може дорівнювати
може дорівнювати
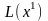 ,
в цьому випадку (див §4)
,
в цьому випадку (див §4)
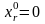 і тому
і тому
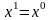 .
В результаті ж кроку симплекс-методу
змінюються лише базис вектори
.
В результаті ж кроку симплекс-методу
змінюються лише базис вектори
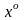 .
Це може призвести до того, що протягом
низки спроб симплекс-методом буде
розглядатися одна і та ж величина, а
змінюватимуться лише базисні вектори,
що відповідають нульовим базисним
змінним і можливе повернення до
початкового базису.
.
Це може призвести до того, що протягом
низки спроб симплекс-методом буде
розглядатися одна і та ж величина, а
змінюватимуться лише базисні вектори,
що відповідають нульовим базисним
змінним і можливе повернення до
початкового базису.
Таке
явище називається за циклюванням
симплекс-методу. Незважаючи на те, що
при розв’язувані прикладних задач за
циклювання не зустрічається і що
побудовано лише декілька штучних
прикладів, де це явище має місце, існують
різні методи його попередження (виходу
з циклу), серед яких метод зрушення
запропонований Чирнесом, суть якого
полягає в тому, що заміть вектора В
розглядають вектор
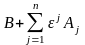 і
(збуджується права частина), що дозволяє
при досить малих
за скінчену кількість кроків симплекс-методу
знайти оптимальний розв’язок ЗЛП зі
збуреною правою частиною вихідної
задачі.
і
(збуджується права частина), що дозволяє
при досить малих
за скінчену кількість кроків симплекс-методу
знайти оптимальний розв’язок ЗЛП зі
збуреною правою частиною вихідної
задачі.
Білет 12