72.Метод ковзної середньої для згладж час ряду

Метод простої ковзної середньої.

Відповідно до цього методу визначається кількість спостережень, що входять в інтервал згладжування, використовуючи правило: якщо необхідно згладити дрібні, безладні коливання, то інтервал згладжування беруть по можливості більшим і, навпаки, інтервал згладжування зменшують, коли потрібно зберегти більш дрібні хвилі і звільнитися від періодично повторюваних коливань, що виникають, наприклад, через автокореляцію рівнів. Обчислюється середнє значення спостережень(парне m)

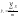
m - кількість спостережень

При непарному m значення параметра значення параметра p обчислюють у такий спосіб: .

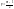p - кількість спостережень, що стоять по різні сторони від спостереження, що згладжується. Інтервал згладжування зміщується на один член вправо знаходиться згладжене значення для t+1 спостереження. Процедура триває доти, поки в інтервал згладжування не ввійде останнє спостереження часового ряду. Недоліком методу є невключення в процедуру згладжування перших і останніх p спостережень часового ряду.Метод простої ковзної середньої можна використати, якщо графічне зображення ряду нагадує пряму лінію, якщо розвиток процесу носить нелінійний характер, то застосування методу простої ковзної середньої може привести до значних перекручувань досліджуваного процесу

Метод зваженої ковзної середньої.

Цей метод відрізняється від попередніх тим, що згладжування всередині інтервалу здійснюється не по прямій, а по кривій більш високого порядку. Це обумовлено тим, що підсумовування членів ряду, що входять в інтервал згладжування, здійснюється з певними вагами, розрахованими по методу найменших квадратів.

73.Експоненційне згладжування

Метод експоненціального згладжування. У процедурі відшукання загладжуваного рівня застосовується значення тільки попередніх рівнів ряду, взятих з певною вагою, яка зменшується при віддалені від кінця ряду. Вага рівнів знижується експоненціально, залежно від параметра згладжування α(0<α<1). Експоненційне згладжування розраховуэться за такою формулою: S_t=α*y_t+(1- α)*S_t-1 де α-параметр згладжування.

74. Аналітичні методи згладжування часового ряду. Метод простої сковзної середньої. Для часового ряду y1,y2,y3… yn визнач. інтервал згладж. m(m<n). Для перших m рівнів часового ряду обчислюється їх сер. арифм. Це буде згладжуване значення рівнів ряду, яке відповідає середині інтервалу згладжув-я. Далі інтервал зсувається на один рівень праворуч, повторюється обчислення сер. арифм. Для обчисл. Згладжених рівнів ряду ýt застосовуэмо формулу: 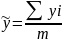. де i - порядковий номер ряду, p=(m-1)/2. Застосований лише для рядів, що мають лінійну тенденцію. Метод експонен-го згладжув-я. У процедурі відшук-я загладж-о рівня застосов-я знач-я тільки попередніх рівнів ряду, взятих з певною вагою, яка зменш-я при віддалені від кінця ряду. Вага рівнів зниж-я експонент-о, залежно від параметра згладжув-я α(0< α<1). Експоненційне згладжув-я розрахов-я за такою формулою: S_t=α*y_t+(1- α)*S_t-1. де α-параметр згладжування.