69.Оцінка адекватн-і і точності трендових моделей.

Перевірка випадковості коливань ривнів послідовності залишків. Для дослідження потрібно розрахувати послідовність залишків Ut=Yt-Ŷt(t=1,n). Метод серій – Крок1-ряд залишків ранжується в порядку зростання і знаходиться медіана. Крок2- кожне значення залишків порівнюється з Ume(утворюється послідовність + та –(серія)). Крок3- визначається загальна кількість серій V і найбільша протяжність однієї з серій Kmax. Крок4 – Для 5%го рівня значущості розраховуються дві нерівності: Kmax<[3,3(lgn+1)] та V > [1/2(n+1-1,96√n-1)]. Якщо хоч 1 нерівн. порушується, трендова модель є неадекватною. Критерій піків – Крок1 – у послідовності залишків вибираються поворотні точки(точка, що більша(менша) двох сусідніх точок). Крок2 – Визначається загальна кількість поворотних точок П. Крок3 – Обчислюється мат сподівання поворотних точок і дисперсія с.428: П = 2/3(n-2); sigma = (16n-29)/90. Крок 4 – критерій випадковості залишків з 5% рівнем знач. має бути виконання нерівності П>[П-1,96√sigma]. Якщо нерівність не виконується, модель неадекватна. Точність характеризується величиною відхилень значень рівнів ряду ха кривою зростання від фактичного рівня. Показники для визначення точності: Середнє квадратичне відхилення σ_u=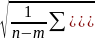 , Середня відносна похибка апроксимації ε_b= . Коефіцієнт збіжності, Коефіцієнт детермінації R^2.

70.Застос-я фіктивних змінних у модел-і сез колив

Фіктивні змінні дозвол позбутися від сезонних коливань у місячних чи квартальних рядах, використовуваних для побудови економетричної моделі. Для виокремл-я сезонних коливань у квартальних рядах, викор-ь матрицю фіктивних змінних, які описують сезонні змінні протягом 4 кварталів.

(1000)

D = (0100)

(0010)

(0001).

Потім будується рівняння залежної змінної Y із сезонними коливаннями, заданими матрицею D: Y = DB+u. Якщо при аналізі один з параметрів фіктивних змінних є істотним, можна вважати за наявний вміст сезонних коливань у часовому ряді.

71.Основні етапи аналізу часових рядів

Аналіз часового ряду почин-я з побудови і вивч-я його графіка. Якщо нестаціонарність часового ряду очевидна, то спочатку необхідно виокрем його нестац-у складову. Крім графіків, ознаками нестаціонарності часового ряду можуть служити автокореляц-а функція, що прямує не до 0 (за винятком дуже великих значень лагів) і наявність яскраво вираж-их піків на низьких частотах у періодограмі. У вибірк-их дослідж-ях найпростіші числові характер-и опис-ої  статистики (середнє, медіана, дисперсія, стандартне відхилення, коефіцієнти асиметрії й ексцесу) звичайно дають достатньо інформативне уявлення про вибірку. Вибір моделі для часового ряду.  Мета цього етапу - опис і урахув-я надалі аналізу кореляційної структури аналізованого процесу. Модель може вважатися підібраною, якщо залишкова компонента ряду є процесом типу, як правило, «білого шуму». Після підбору залишки аналізуються для перевірки адекватності моделі та побудови надійних інтервалів. Прогнозування або інтерполяція. Останнім етапом аналізу часового ряду може бути прогнозування його майбутніх (екстраполяція) або відновлення пропущених (інтерполяція) значень і визначення точності цього прогнозу на базі підібраної моделі. Добре підібрати математичну модель вдається не для всякого часового ряду. Нерідко буває і так, що для опису підходять відразу декілька моделей. Неоднозначність вибору моделі може спостерігатися як на етапі виділення детермінованого компонента ряду, так і при виборі структури ряду залишків. Тому досить часто розробляють декілька прогнозів, зроблених за допомогою різних моделей.