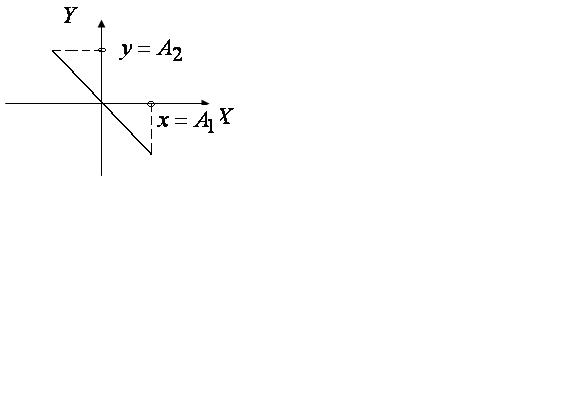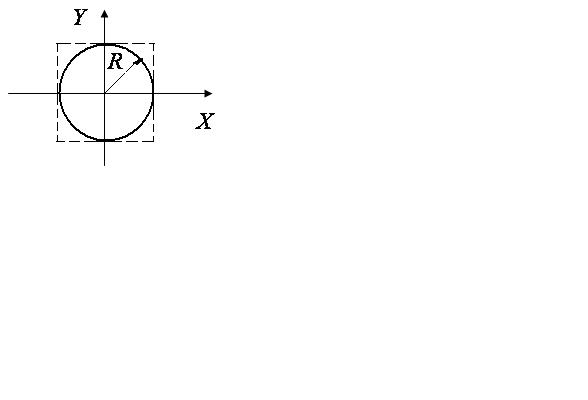- •Введение
- •Элементарные частицы атомы молекулы тела
- •Классификация медицинской электронной аппаратуры
- •Классификация медицинской электроники по функциональному назначению.
- •II. Классификация медицинской аппаратуры по принципу действия.
- •Действие электрического тока на организм.
- •От вида тока и частоты.
- •Обеспечение электробезопасности при работе с медицинской аппаратурой.
- •Классификация медицинской аппаратуры по способу дополнительной защиты от поражающего действия электрического тока.
- •Надежность медицинской аппаратуры
- •Механические колебания
- •Незатухающие колебания
- •Энергия колеблющейся точки
- •Затухающие колебания
- •Вынужденные колебания
- •Автоколебания
- •Сложение колебаний
- •I.Однонаправленные колебания.
- •2. Взаимноперпендикулярные колебания.
- •Сложное колебание. Гармонический спектр сложного колебания.
- •Механические волны.
- •Уравнение плоской механической волны.
- •Энергия волны. Поток энергии волны. Вектор Умова.
- •Эффект Доплера.
- •Акустика. Природа звука.
- •Физические характеристики звука.
- •Характеристики слухового ощущения (Физиологические характеристики).
- •Шкала уровней громкости.
- •Звуковые методы исследования в клинике.
- •Гидродинамика
- •Свойства жидкостей
- •Основные понятия гидродинамики
- •Уравнение неразрывности струи
- •Уравнение Бернулли
- •Практические следствия из уравнения Бернулли.
- •Определение гидростатического давления
- •Правило Бернулли
- •4.Всасывающее действие струи – водоструйный насос.
- •Вязкость жидкости.
- •Ламинарное и турбулентное течение
- •Течение реальной жидкости по горизонтальной трубе постоянного сечения. Закон Гагена-Пуазейля.
- •Течение жидкости по горизонтальной трубе переменного сечения
- •Течение жидкости по разветвленной трубе
- •Течение жидкости по эластичной трубе
- •Биореология.
- •О т градиента скорости (скорости сдвига)
- •2) От гематокритного показателя (гематокрита) ,
- •3) От температуры
- •От диаметра сосуда, по которому течет кровь
- •Физические модели кровообращения.
- •Гидродинамическая
- •Электрическая модель.
- •Закономерности выброса и распространения крови в большом круге кровообращения.
- •Работа и мощность сердца.
- •Биологические мембраны
- •2.Физические свойства мембран.
- •Методы исследования мембран
- •4. Рентгеноструктурный анализ.
- •Диффузия в жидкостях. Закон Фика
- •Транспорт веществ через мембрану.
- •Пассивный транспорт веществ.
- •Перенос незаряженных частиц (атомов и молекул) через мембрану
- •Перенос заряженных частиц (ионов) через мембрану
- •Облегченная диффузия.
- •Активный транспорт.
- •Потенциал действия.
- •Распространение потенциала действия. (проведение возбуждения по нервным волокнам).
- •Электромагнитные явления в биологических системах Природа биопотенциалов и способы их описания
- •Равенство Доннана.
- •Потенциал покоя
- •Потенциал действия.
- •Распространение потенциала действия. (проведение возбуждения по нервным волокнам).
- •Биофизические принципы исследования Электрических полей в организме.
- •Электрический диполь
- •Напряженность электрического поля диполя.
- •Потенциал. Разность потенциалов.
- •Диполь в электрическом поле.
- •Токовый диполь. Эквивалентный электрический генератор.
- •Электрокардиография
- •Метод отведений Эйнтховена
- •Вектор-электрокардиография.
- •Незатухающие электромагнитные колебания.
- •Затухающие колебания
- •Вынужденные колебания.
- •Импульсные токи
- •Апериодический разряд конденсатора
- •Характеристики импульсных токов.
- •Генераторы импульсных токов.
- •Генератор на неоновой лампе
- •Блокинг-генератор
- •3. Мультивибратор
- •Изменение формы импульса.
- •Дифференцирующая цепь
- •Действие импульсного тока на ткани организма
- •Биологические основы реографии
- •Цпт, содержащая последовательно включенные активное, индуктивное и ёмкостное сопротивления
- •Цпт, содержащая параллельно включенные активное, индуктивное и ёмкостное сопротивления
- •Органы и ткани как элементы цптю
- •Электромагнитное поле. Электромагнитные волны Основные положения электромагнитной теории Максвелла.
- •Энергия электромагнитной волны
- •Физические процессы, происходящие в тканях организма под действием токов и электромагнитного поля
- •3. Переменное магнитное поле.
- •Поляризация света Природа света. Основные характеристики света
- •Поляризация света
- •Методы получения полностью поляризованного света
- •При отражении от неметаллического зеркала
- •При двойном лучепреломлении
- •3. Дихроизм.
- •Система поляризатор – анализатор
- •Вращение плоскости поляризации. Поляриметрия
- •Поляризационный микроскоп
- •Тепловое излучение. Природа теплового излучения. Характеристики теплового излучения
- •Закон Кирхгофа
- •Законы излучения абсолютно черного тела
- •Формула Планка и её применение для уточнения законов теплового излучения абсолютно черного тела
- •Источники теплового излучения, применяемые для лечебных целей
- •Электронная оптика Волновые свойства частиц. Длина волны де Бройля
- •Электронный микроскоп
- •Люминесценция
- •Фотолюминесценция
- •Закон Стокса
- •Количественные оценки люминесценции
- •Применение люминесценции в медицине
- •Индуцированное излучение. Лазеры – оптические квантовые генераторы
- •Свойства лазерного излучения
- •Применение лазеров в медицине
- •Голография и возможности её применения в медицине
- •Рентгеновское излучение
- •Свойства рентгеновского излучения
- •Механизмы генерации рентгеновского излучения
- •Рентгеновская трубка
- •Зависимость энергии рентгеновского излучения от рабочих параметров рентгеновской трубки.
- •Действие рентгеновского излучения на вещество
- •Некогерентное рассеяние (эффект Комптона).
- •Применение рентгеновского излучения в медицине
- •Ионизирующее излучение
- •Строение атомного ядра
- •Энергия связи
- •Радиоактивность. Виды излучений
- •Основной закон радиоактивного распада
- •Радиоактивность в природе – естественная фоновая радиация
- •Дозиметрия ионизирующего излучения Проникающая и ионизирующая способности радиоактивного излучения
- •Биофизические основы действия ионизирующего излучения на организм
- •Характеристики ионизирующего излучения
- •Дозиметрическая аппаратура
- •Защита от ионизирующего излучения
- •Электронный парамгнитный резонанс
- •Ядерный магнитный резонанс
Автоколебания
Мы выяснили, что амплитуда вынужденных колебаний зависит от амплитуды и частоты внешней, вынуждающей, силы.
Это означает, что внешнее воздействие “управляет” колебаниями системы и сообщает ей энергию, не согласовываясь с процессами, происходящими в системе. Можно создать такую систему, в которой вынужденные колебания происходят с собственной частотой. Такие системы называются автоколебательными, а происходящие в них колебания - автоколебаниями.
Механическая автоколебательная система содержит источник внешней силы, постоянной по величине и направлению, которая периодически в необходимые моменты “подталкивает” колеблющееся тело и таким образом поддерживает его свободные колебания незатухающими. Блок-схема автоколебательной системы представлена на рис. 2.8.
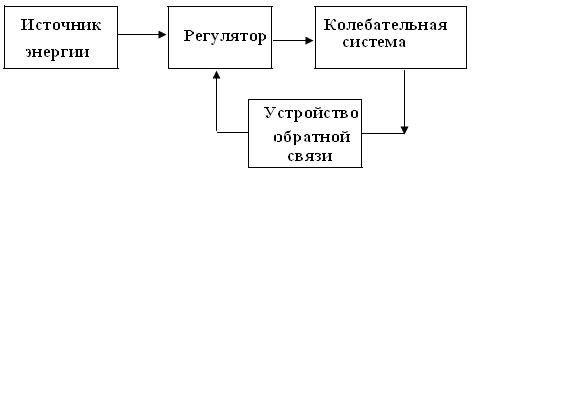
Рис. 2.8.
Сложение колебаний
Колебательное движение, при котором смещение описывается во времени любым законом, но не законом синуса или косинуса, является сложным колебанием. Сложное колебание – это результат сложения простых, гармонических, колебаний. Поэтому мы должны уметь складывать колебания.
Смещение тела, участвующего одновременно в двух или нескольких колебаниях, находится на основании принципа суперпозиции, согласно которому эти колебания накладываются, не влияя одно на другое.
I.Однонаправленные колебания.
Пусть материальная точка одновременно участвует в двух колебаниях, происходящих вдоль одной линии. Смещения этой точки для каждого колебания описывается уравнениями
![]() ,
,
![]()
а)
Если
![]() ;
;
![]() ,
но
,
но
![]() то
смещение результирующего колебания
описывается как
то
смещение результирующего колебания
описывается как
![]() .
.
б) В общем случае при условии, что ,
![]() ,
,
сложение удобнее проводить с использованием
метода векторных диаграмм.
,
,
сложение удобнее проводить с использованием
метода векторных диаграмм.
При указанных условиях смещения точки запишутся как
![]() ,
,
![]() ,
,
а смещение результирующего колебания определится как
![]() .
.
Смещение результирующего колебания будем описывать уравнением
![]()
Для
расчета амплитуды
![]() результирующего колебания построим
векторную диаграмму. Из точки
результирующего колебания построим
векторную диаграмму. Из точки
![]() системы координат ХОУ (рис.2.9) проведем
векторы
системы координат ХОУ (рис.2.9) проведем
векторы
![]() и
и
![]() под углами
под углами
![]() и
и
![]() к оси ОХ, соответственно. Длины этих
векторов равны модулям амплитуд
и
складывающихся колебаний. Векторы
к оси ОХ, соответственно. Длины этих
векторов равны модулям амплитуд
и
складывающихся колебаний. Векторы
![]() и
вращаются с одинаковой частотой,
следовательно, вектор
будет вращаться с той же частотой.
и
вращаются с одинаковой частотой,
следовательно, вектор
будет вращаться с той же частотой.
А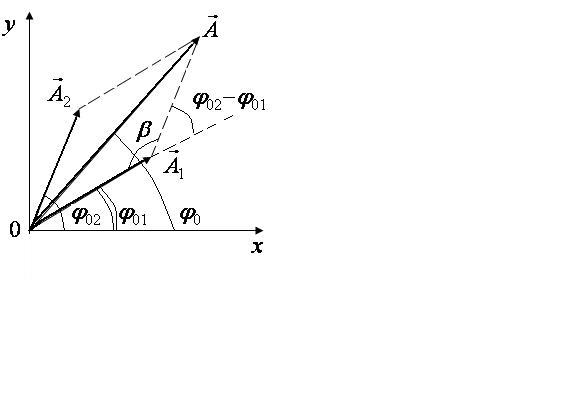 мплитуду
результирующего колебания найдем из
треугольника
мплитуду
результирующего колебания найдем из
треугольника
![]() ,
применив теорему косинусов
,
применив теорему косинусов
![]() Т.к.
Т.к.![]() ,
,
то![]()
рис. 2.9
Начальная
фаза
![]() результирующего колебания находится
как
результирующего колебания находится
как
![]() =
=![]() =
=![]() .
.
Частные случаи:
1)
![]() ,
,![]() ,
,
где
![]()
Тогда
![]() -
усиление колебаний (рис.2.10):
-
усиление колебаний (рис.2.10):
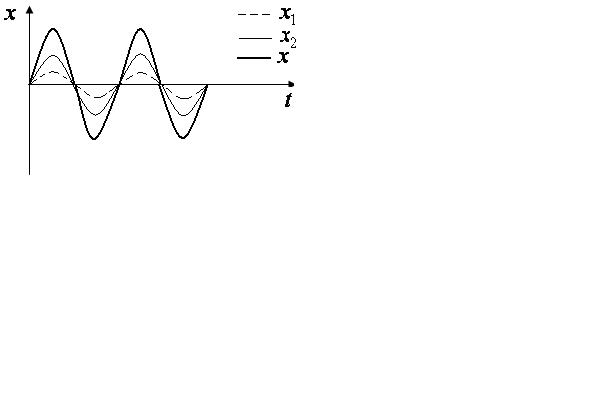
Рис. 2.10
2)
![]() ,
,![]()
Тогда
![]() - ослабление колебаний (рис.2.11):
- ослабление колебаний (рис.2.11):
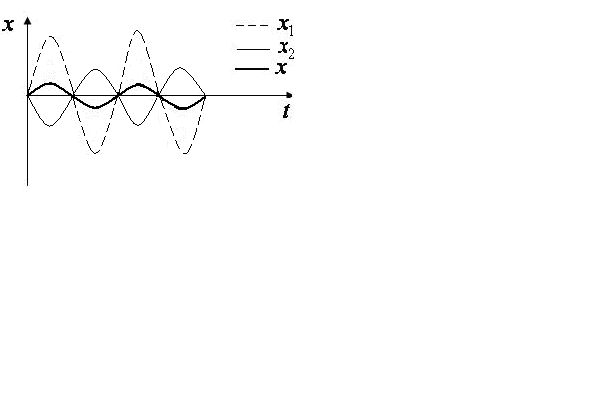
Рис. 2.11
Биения.
Если частоты слагаемых колебаний мало
отли-чаются, т.е.
![]() ,
то результирующее колебание будет
подобно гармоническому колебанию с
медленно изменяющейся амплитудой.
Наблюдается амплитудная модуляция.
Такие колебания называются биениями
(рис. 2.12)
,
то результирующее колебание будет
подобно гармоническому колебанию с
медленно изменяющейся амплитудой.
Наблюдается амплитудная модуляция.
Такие колебания называются биениями
(рис. 2.12)
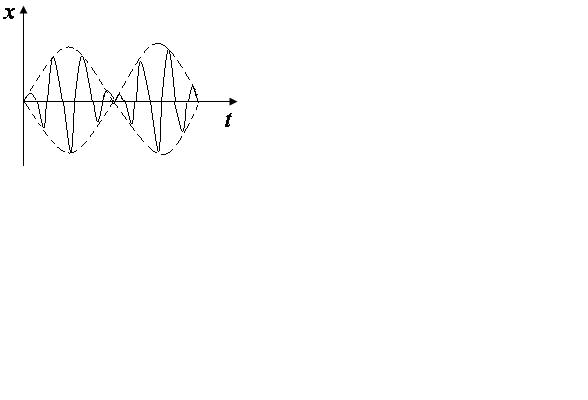
Рис. 2.12
2. Взаимноперпендикулярные колебания.
Возможна ситуация, при которой точка участвует одновременно в двух взаимноперпендикулярных колебаниях: одно направлено вдоль оси ОХ, другое - вдоль оси ОУ. Смещения точек описываются при этом уравнениями (считаем, что собственная частота у обоих колебаний одинакова):
![]() ,
,
![]() .
.
Исключая из этих уравнений время t, получим уравнение
![]() в
виде
в
виде
![]()

Это и есть уравнение траектории, по которой движется точка, а именно, уравнение эллипса (рис.2.13).
Рис. 2.13
Конкретный
вид траектории зависит от разности фаз
![]() .
Если
.
Если
![]() ,
где
,
где
![]() ,
,
то
![]() ,
и уравнение (2.16) запишется как
,
и уравнение (2.16) запишется как
![]()
или после преобразований
![]() ,
,![]() ,
,
![]() ,
,
т.е.
получаем уравнения прямой, по которой
будет двигаться точка (рис.2.11 соответствует
знаку
![]() ,
рис.2.12 соответствует знаку -).
,
рис.2.12 соответствует знаку -).
|
|
Рис.2.11 |
Рис.2.12 |
Если
![]() ,
то
,
то
![]() ,
,
![]() ,
и уравнение (2.16) запишется как
,
и уравнение (2.16) запишется как
![]()
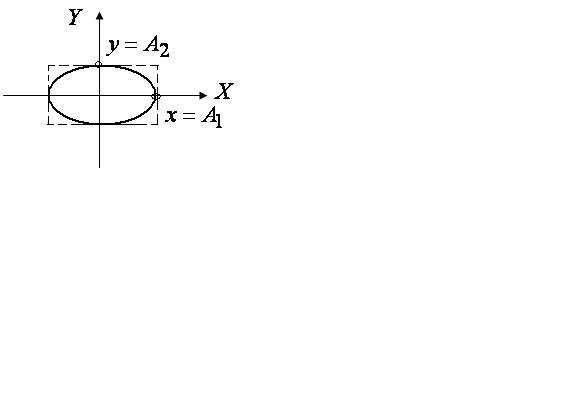
Это уравнение эллипса, расположенного симметрично относительно осей координат. Именно такую траекторию будет описывать точка (рис. 2.13).
Если
при такой разности фаз,
,
амплитуды равны между собой (![]() ),
то уравнение (2.17) станет уравнением
окружности (рис. 2.14).
),
то уравнение (2.17) станет уравнением
окружности (рис. 2.14).
![]()
|
|
Рис. 2.13 |
Рис. 2.14 |
Траектории, по которым движется точка в результате сложения колебаний, называются фигурами Лиссажу.