Энергия колеблющейся точки
Полная
энергия колеблющейся точки складывается
из ее потенциальной,
.,
и кинетической энергии,
:
Если смещение точки описывается уравнением
,
то
,
то потенциальная энергия определиться
как
т.к.
,
а кинетическая энергия определиться
как
.
Полная энергия, таким образом, определяется как
откуда
Затухающие колебания
Реальные механические колебания, т.е. колебания, происхо-дящие в природе, совершаются в среде. Значит, на колеблющуюся точку кроме возвращающей силы действует еще сила трения:
,
где
– коэффициент трения. Следовательно,
реальные колебания являются затухающими,
т.к. энергия колеблющейся точки теряется
на преодоление силы трения.
Теперь уравнение движения колеблющейся точки следует записать в виде
или в скалярном виде в проекциях на ось ОХ
.
Заменяя
и
через производные,
получим
.
Деля
на
обе части уравнения и вводя обозначения
(
- коэффициент затухания) и
,
получим дифференциальное уравнение
второго порядка для затухающих колебаний
.
Решением этого уравнения является функция
или
.
Здесь
– амплитуда
первого колебания.
Анализируя решение, следует отметить, что амплитуда затухающих колебаний с течением времени уменьшается с течением времени по экспоненциальному закону из-за потерь энергии точки на преодоление силы трения и определяется в любой момент времени как
.
Само
же колебание остается гармоническим и
происходит с периодом
.
График зависимости смещения затухающего
колебания от времени приведен на рис.
2.5.
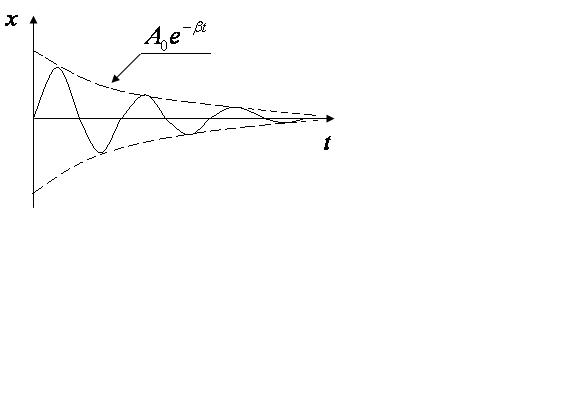
Рис. 2.5
Быстроту затухания, т.е. быстроту убывания амплитуды, определяют логарифмическим декрементом затухания
или,
после подстановки в это отношение
значений амплитуд в моменты времени
и
,
.
Вынужденные колебания
Чтобы
компенсировать потери энергии на
преодоление силы трения, необходимо
колеблющейся точке извне добавлять
энергию, т.е. необходимо действовать на
точку внешней вынуж-дающей силой
.
Эта сила должна удовлетворять следующим
требованиям: она должна быть периодической
и иметь частоту
,
отличную от частоты собственных колебаний
точки,
,
т.е. её можно записать как
где
-
амплитуда вынуждающей силы.
Следовательно,
при вынужденных колебаниях точка
движется под действием равнодействующей
сил
и
.
Уравнение движения теперь запишется в
виде
или
в проекциях на ось
.
После деления на m и введения применяемых ранее обозначений, получим дифференциальное уравнение 2-го порядка для вынужденных колебаний
.
Решением этого уравнения является функция
.
Точнее
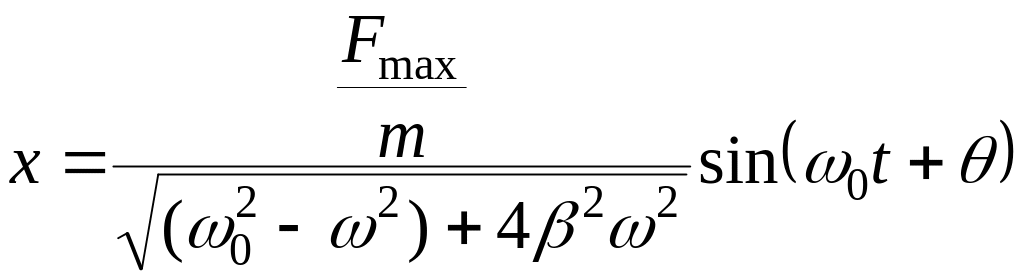
Здесь
– амплитуда вынужденных колебаний.
Как видим, она зависит от частоты и
амплитуды вынуждающей силы. Анализируя
решение, замечаем, что колебания точки
происходят с частотой вынуждающей силы,
колебание остается гармоническим с
новой начальной фазой
.
Если коэффициент затухания стремится к нулю (это возможно при малом сопротивлении), то
График смещения вынужденных колебаний показан на рис.2.6. Начальный период мы не рассматриваем. Все проведенные выше рассуждения касались только установившихся вынужденных колебаний.
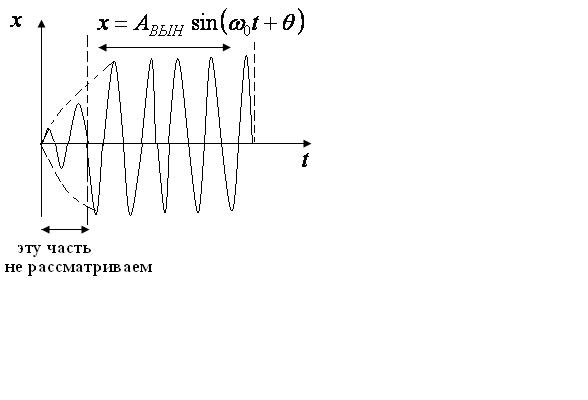
График зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы при различных коэффициентах затухания показан на рис.2.7.
Рис. 2.6
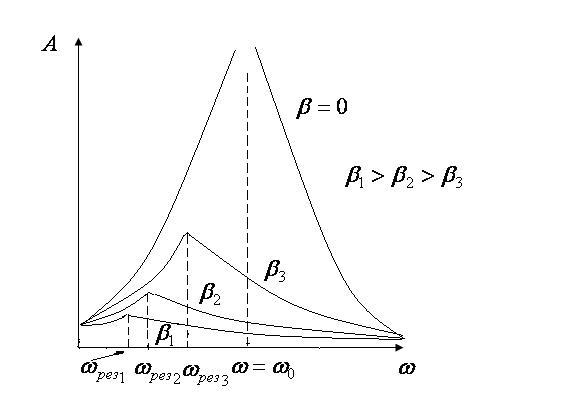
Рис.2.7
При
выполнении условия
амплитуда
резко возрастает
.
Это явление резкого возрастания амплитуды
при равенстве собственной частоты
колебаний точки и частоты вынуждающей
силы называется явлением механического
резонанса.
Явление механического резонанса может быть полезным: при малых усилиях можно увеличить амплитуду колебания; но может быть и вредным: разрушение, действие вибраций на организм. Предупреждают резозанс тем, что создают колебания с частотой , отличной от частоты вынуждающей силы.