1.5.2. Response Surface Analysis Methods

For response surface analysis, you can choose from three sampling methods: Central Composite Design, Box-Behnken Matrix, and user-defined.

Response surface methods are based on the fundamental assumption that the influence of the random input variables on the random output parameters can be approximated by mathematical function. Hence, Response Surface Methods locate the sample points in the space of random input variables such that an appropriate approximation function can be found most efficiently; typically, this is a quadratic

where c0 is the coefficient of the constant term, ci, i = 1,...NRV are the coefficients of the linear terms and cij, i = 1,...NRV and j = i, ...,NRV are the coefficients of the quadratic terms. To evaluate these coefficients a regression analysis is used and the coefficients are usually evaluated such that the sum of squared differences between the true simulation results and the values of the approximation function is minimized.

Hence, a response surface analysis consists of two steps:

1.Performing the simulation loops to calculate the values of the random output parameters that correspond to the sample points in the space of random input variables.

2.Performing a regression analysis to derive the terms and the coefficients of the approximation function.

The fundamental idea of Response Surface Methods is that once the coefficients of a suitable approximation function are found, then we can directly use the approximation function instead of looping through the finite element model. To perform a finite element analysis might require minutes to hours of computation time; in contrast, evaluating a quadratic function requires only a fraction of a second. Hence, if using the approximation function, we can afford to evaluate the approximated response parameter thousands of times.

A quadratic polynomial is sufficient in many cases of engineering analysis (for example, the evaluation of the thermal stress mentioned above). For that evaluation, the Young's modulus and the thermal expansion coefficient both have a linear effect on the thermal stresses, which is taken into account in a quadratic approximation by the mixed quadratic terms. However, there are cases where a quadratic approximation is not sufficient; for example, if the finite element results are used to calculate the lifetime of a component. For this evaluation, the lifetime typically shows an exponential behavior with respect

to the input parameters; thus the lifetime results cannot be directly or sufficiently described by a quadratic polynomial. But often, if you apply a logarithmic transformation to the lifetime results, then these transformed values can be approximated by a quadratic polynomial. The ANSYS PDS offers a

vk.com/club152685050Probabi istic Design | vk.com/id446425943

variety of transformation functions that you can apply to the response parameters, and the logarithmic transformation function is one of them.

Assuming the approximation function is suitable for your problem, the advantages of the Response Surface Method are:

•It often requires fewer simulation loops than the Monte Carlo Simulation method.

•It can evaluate very low probability levels. This is something the Monte Carlo Simulation method cannot do unless you perform a great number of simulation loops.

•The goodness-of-fit parameters tell you how good the approximation function is (in other words, how accurate the approximation function is that describes your "true" response parameter values). The goodness-of-fit parameters can warn you if the approximation function is insufficient.

•The individual simulation loops are inherently independent (the individual simulation loops do not depend on the results of any other simulation loops). This makes Response Surface Method an ideal candidate for parallel processing.

The disadvantages of the Response Surface Method are:

•The number of required simulation loops depends on the number of random input variables. If you have a very large number of random input variables (hundreds or even thousands), then a probabilistic analysis using Response Surface Methods would be impractical.

•This method is not usually suitable for cases where a random output parameter is a non-smooth function of the random input variables. For example, a non-smooth behavior is given if you observe a sudden jump of the output parameter value even if the values for the random input variables vary only slightly. This typically occurs if you have instability in your model (such as bulking). The same might happen if the model includes a sharp nonlinearity such as a linear-elastic-ideal-plastic material behavior. Or, if you are analyzing a contact problem, where only a slight variation in your random input variables can change the contact situation from contact to non-contact or vice versa, then you also might have problems using the Response Surface Method.

Note

To use Response Surface Methods, the random output parameters must be smooth and continuous functions of the involved random input variables. Do not use Response Surface Methods if this condition is not satisfied.

1.5.2.1. Central Composite Design Sampling

A central composite design consists of a central point, the N axis point plus 2N-f factorial points located at the corners of an N-dimensional hypercube. Here, N is the number of random input variables and f is the fraction of the factorial part of the central composite design. A fraction f = 0 is a called a full factorial design, f = 1 gives a half-factorial design, and so on. The PDS gradually increases the fraction

f as you increase the number of random input variables. This keeps the number of simulation loops reasonable. The fraction f is automatically evaluated such that a resolution V design is always maintained. A resolution V design is a design where none of the second order terms of the approximation function are confined with each other. This ensures a reasonable accuracy for the evaluation of the coefficients

of the second order terms.

The locations of the sampling points for a problem with three random input variables is illustrated below.

Figure 1.9: Locations of Sampling Points for Problem with Three Input Variables for CCD

The number of sample points (simulation loops) required for a central composite design as a function of the number of random input variables is given in the table below:

To use the Response Surface Method with a Central Composite Design, do the following:

Command(s): PDMETH,RSM,CCD PDDOEL,Name,CCD,...

GUI: Main Menu> Prob Design> Prob Method> Response Surface

PDDOEL allows you to specify design of experiment options.

See the Mechanical APDL Theory Reference for more details.

vk.com/club152685050Probabi istic Design | vk.com/id446425943

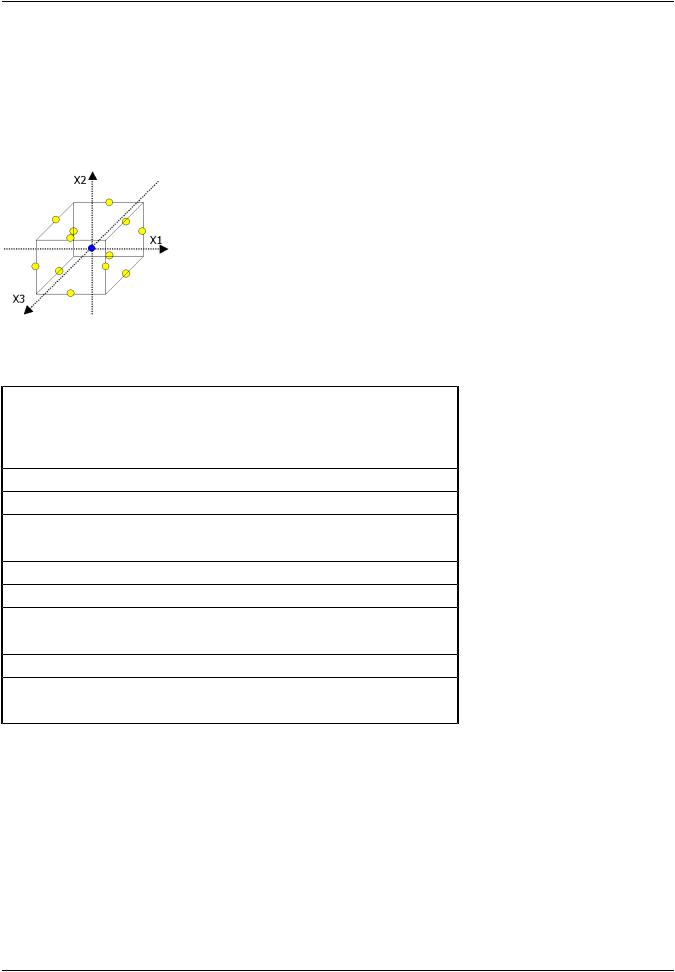
1.5.2.2. Box-Behnken Matrix Sampling

A Box-Behnken Design consists of a central point plus the midpoints of each edge of an N-dimensional hypercube.

The location of the sampling points for a problem with three random input variables is illustrated below.

Figure 1.10: Location of Sampling Points for Problem with Three Input Variables for BBM

The number of sample points (simulation loops) required for a Box-Behnken design as a function of the number of random input variables is given in the table below:

To use Response Surface Analysis with the Box-Behnken design option, do the following:

Command(s): PDMETH,RSM,BBM PDDOEL,Name,BBM,...

GUI: Main Menu> Prob Design> Prob Method> Response Surface

PDDOEL allows you to specify design of experiment options.

See the Mechanical APDL Theory Reference for more details.

1.5.2.3. User-Defined Sampling

For this method, you provide the file containing the samples.