
- •Table of Contents
- •Chapter 1: Probabilistic Design
- •1.1. Understanding Probabilistic Design
- •1.1.1. Traditional (Deterministic) vs. Probabilistic Design Analysis Methods
- •1.1.2. Reliability and Quality Issues
- •1.2. Probabilistic Design Terminology
- •1.3. Using Probabilistic Design
- •1.3.1. Create the Analysis File
- •1.3.1.1. Example Problem Description
- •1.3.1.2. Build the Model Parametrically
- •1.3.1.3. Obtain the Solution
- •1.3.1.4. Retrieve Results and Assign as Output Parameters
- •1.3.1.5. Prepare the Analysis File
- •1.3.2. Establish Parameters for Probabilistic Design Analysis
- •1.3.3. Enter the PDS and Specify the Analysis File
- •1.3.4. Declare Random Input Variables
- •1.3.5. Visualize Random Input Variables
- •1.3.6. Specify Correlations Between Random Variables
- •1.3.7. Specify Random Output Parameters
- •1.3.8. Select a Probabilistic Design Method
- •1.3.8.1. Probabilistic Method Determination Wizard
- •1.3.9. Execute Probabilistic Analysis Simulation Loops
- •1.3.9.1. Probabilistic Design Looping
- •1.3.9.2. Serial Analysis Runs
- •1.3.9.3. PDS Parallel Analysis Runs
- •1.3.9.3.1. Machine Configurations
- •1.3.9.3.1.1. Choosing Slave Machines
- •1.3.9.3.1.2. Using the Remote Shell Option
- •1.3.9.3.1.3. Using the Connection Port Option
- •1.3.9.3.1.4. Configuring the Master Machine
- •1.3.9.3.1.5. Host setup using port option
- •1.3.9.3.1.6. Host and Product selection for a particular analysis
- •1.3.9.3.2. Files Needed for Parallel Run
- •1.3.9.3.3. Controlling Server Processes
- •1.3.9.3.4. Initiate Parallel Run
- •1.3.10. Fit and Use Response Surfaces
- •1.3.10.1. About Response Surface Sets
- •1.3.10.2. Fitting a Response Surface
- •1.3.10.3. Plotting a Response Surface
- •1.3.10.4. Printing a Response Surface
- •1.3.10.5. Generating Monte Carlo Simulation Samples on the Response Surfaces
- •1.3.11. Review Results Data
- •1.3.11.1. Viewing Statistics
- •1.3.11.2. Viewing Trends
- •1.3.11.3. Creating Reports
- •1.4. Guidelines for Selecting Probabilistic Design Variables
- •1.4.1. Choosing and Defining Random Input Variables
- •1.4.1.1. Random Input Variables for Monte Carlo Simulations
- •1.4.1.2. Random Input Variables for Response Surface Analyses
- •1.4.1.3. Choosing a Distribution for a Random Variable
- •1.4.1.3.1. Measured Data
- •1.4.1.3.2. Mean Values, Standard Deviation, Exceedence Values
- •1.4.1.3.3. No Data
- •1.4.1.4. Distribution Functions
- •1.4.2. Choosing Random Output Parameters
- •1.5. Probabilistic Design Techniques
- •1.5.1. Monte Carlo Simulations
- •1.5.1.1. Direct Sampling
- •1.5.1.2. Latin Hypercube Sampling
- •1.5.1.3. User-Defined Sampling
- •1.5.2. Response Surface Analysis Methods
- •1.5.2.1. Central Composite Design Sampling
- •1.5.2.2. Box-Behnken Matrix Sampling
- •1.5.2.3. User-Defined Sampling
- •1.6. Postprocessing Probabilistic Analysis Results
- •1.6.1. Statistical Postprocessing
- •1.6.1.1. Sample History
- •1.6.1.2. Histogram
- •1.6.1.3. Cumulative Distribution Function
- •1.6.1.4. Print Probabilities
- •1.6.1.5. Print Inverse Probabilities
- •1.6.2. Trend Postprocessing
- •1.6.2.1. Sensitivities
- •1.6.2.2. Scatter Plots
- •1.6.2.3. Correlation Matrix
- •1.6.3. Generating an HTML Report
- •1.7. Multiple Probabilistic Design Executions
- •1.7.1. Saving the Probabilistic Design Database
- •1.7.2. Restarting a Probabilistic Design Analysis
- •1.7.3. Clearing the Probabilistic Design Database
- •1.8. Example Probabilistic Design Analysis
- •1.8.1. Problem Description
- •1.8.2. Problem Specifications
- •1.8.2.1. Problem Sketch
- •1.8.3. Using a Batch File for the Analysis
- •1.8.4. Using the GUI for the PDS Analysis
- •Chapter 2: Variational Technology
- •2.1. Harmonic Sweep Using VT Accelerator
- •2.1.1. Structural Elements Supporting Frequency-Dependent Properties
- •2.1.2. Harmonic Sweep for Structural Analysis with Frequency-Dependent Material Properties
- •2.1.2.1. Beam Example
- •Chapter 3: Adaptive Meshing
- •3.1. Prerequisites for Adaptive Meshing
- •3.2. Employing Adaptive Meshing
- •3.3. Modifying the Adaptive Meshing Process
- •3.3.1. Selective Adaptivity
- •3.3.2. Customizing the ADAPT Macro with User Subroutines
- •3.3.2.1. Creating a Custom Meshing Subroutine (ADAPTMSH.MAC)
- •3.3.2.2. Creating a Custom Subroutine for Boundary Conditions (ADAPTBC.MAC)
- •3.3.2.3. Creating a Custom Solution Subroutine (ADAPTSOL.MAC)
- •3.3.2.4. Some Further Comments on Custom Subroutines
- •3.3.3. Customizing the ADAPT Macro (UADAPT.MAC)
- •3.4. Adaptive Meshing Hints and Comments
- •3.5. Where to Find Examples
- •Chapter 4: Rezoning
- •4.1. Benefits and Limitations of Rezoning
- •4.1.1. Rezoning Limitations
- •4.2. Rezoning Requirements
- •4.3. Understanding the Rezoning Process
- •4.3.1. Overview of the Rezoning Process Flow
- •4.3.2. Key Commands Used in Rezoning
- •4.4. Step 1: Determine the Substep to Initiate Rezoning
- •4.5. Step 2. Initiate Rezoning
- •4.6. Step 3: Select a Region to Remesh
- •4.7. Step 4: Perform the Remeshing Operation
- •4.7.1. Choosing a Remeshing Method
- •4.7.1.1. Remeshing Using a Program-Generated New Mesh (2-D)
- •4.7.1.1.1. Creating an Area to Remesh
- •4.7.1.1.2. Using Nodes From the Old Mesh
- •4.7.1.1.3. Hints for Remeshing Multiple Regions
- •4.7.1.1.4. Generating a New Mesh
- •4.7.1.2. Remeshing Using a Generic New Mesh (2-D and 3-D)
- •4.7.1.2.1. Using the REMESH Command with a Generic New Mesh
- •4.7.1.2.2. Requirements for the Generic New Mesh
- •4.7.1.2.3. Using the REGE and KEEP Remeshing Options
- •4.7.1.3. Remeshing Using Manual Mesh Splitting (2-D and 3-D)
- •4.7.1.3.1. Understanding Mesh Splitting
- •4.7.1.3.2. Geometry Details for Mesh Splitting
- •4.7.1.3.3. Using the REMESH Command for Mesh Splitting
- •4.7.1.3.4. Mesh-Transition Options for 2-D Mesh Splitting
- •4.7.1.3.5. Mesh-Transition Options for 3-D Mesh Splitting
- •4.7.1.3.7. Improving Tetrahedral Element Quality via Mesh Morphing
- •4.7.2. Mesh Control
- •4.7.3. Remeshing Multiple Regions at the Same Substep
- •4.8. Step 5: Verify Applied Contact Boundaries, Surface-Effect Elements, Loads, and Boundary Conditions
- •4.8.1. Contact Boundaries
- •4.8.2. Surface-Effect Elements
- •4.8.3. Pressure and Contiguous Displacements
- •4.8.4. Forces and Isolated Applied Displacements
- •4.8.5. Nodal Temperatures
- •4.8.6. Other Boundary Conditions and Loads
- •4.9. Step 6: Automatically Map Variables and Balance Residuals
- •4.9.1. Mapping Solution Variables
- •4.9.2. Balancing Residual Forces
- •4.9.3. Interpreting Mapped Results
- •4.9.4. Handling Convergence Difficulties
- •4.10. Step 7: Perform a Multiframe Restart
- •4.11. Repeating the Rezoning Process if Necessary
- •4.11.1. File Structures for Repeated Rezonings
- •4.12. Postprocessing Rezoning Results
- •4.12.1. The Database Postprocessor
- •4.12.1.1. Listing the Rezoning Results File Summary
- •4.12.1.2. Animating the Rezoning Results
- •4.12.1.3. Using the Results Viewer for Rezoning
- •4.12.2. The Time-History Postprocessor
- •4.13. Rezoning Restrictions
- •4.14. Rezoning Examples
- •4.14.1. Example: Rezoning Using a Program-Generated New Mesh
- •4.14.1.1. Initial Input for the Analysis
- •4.14.1.2. Rezoning Input for the Analysis
- •4.14.2. Example: Rezoning Using a Generic New Mesh
- •4.14.2.1. Initial Input for the Analysis
- •4.14.2.2. Exporting the Distorted Mesh as a CDB File
- •4.14.2.3. Importing the File into ANSYS ICEM CFD and Generating a New Mesh
- •4.14.2.4. Rezoning Using the New CDB Mesh
- •Chapter 5: Mesh Nonlinear Adaptivity
- •5.1. Mesh Nonlinear Adaptivity Benefits, Limitations and Requirements
- •5.1.1. Rubber Seal Simulation
- •5.1.2. Crack Simulation
- •5.2. Understanding the Mesh Nonlinear Adaptivity Process
- •5.2.1. Checking Nonlinear Adaptivity Criteria
- •5.2.1.1. Defining Element Components
- •5.2.1.2. Defining Nonlinear Adaptivity Criteria
- •5.2.1.3. Defining Criteria-Checking Frequency
- •5.3. Mesh Nonlinear Adaptivity Criteria
- •5.3.1. Energy-Based
- •5.3.2. Position-Based
- •5.3.3. Contact-Based
- •5.3.4. Frequency of Criteria Checking
- •5.4. How a New Mesh Is Generated
- •5.5. Convergence at Substeps with the New Mesh
- •5.6. Controlling Mesh Nonlinear Adaptivity
- •5.7. Postprocessing Mesh Nonlinear Adaptivity Results
- •5.8. Mesh Nonlinear Adaptivity Examples
- •5.8.1. Example: Rubber Seal Simulation
- •5.8.2. Example: Crack Simulation
- •Chapter 6: 2-D to 3-D Analysis
- •6.1. Benefits of 2-D to 3-D Analysis
- •6.2. Requirements for a 2-D to 3-D Analysis
- •6.3. Overview of the 2-D to 3-D Analysis Process
- •6.3.1. Overview of the 2-D to 3-D Analysis Process Flow
- •6.3.2. Key Commands Used in 2-D to 3-D Analysis
- •6.4. Performing a 2-D to 3-D Analysis
- •6.4.1. Step 1: Determine the Substep to Initiate
- •6.4.2. Step 2: Initiate the 2-D to 3-D Analysis
- •6.4.3. Step 3: Extrude the 2-D Mesh to the New 3-D Mesh
- •6.4.4. Step 4: Map Solution Variables from 2-D to 3-D Mesh
- •6.4.5. Step 5: Perform an Initial-State-Based 3-D Analysis
- •6.5. 2-D to 3-D Analysis Restrictions
- •Chapter 7: Cyclic Symmetry Analysis
- •7.1. Understanding Cyclic Symmetry Analysis
- •7.1.1. How the Program Automates a Cyclic Symmetry Analysis
- •7.1.2. Commands Used in a Cyclic Symmetry Analysis
- •7.2. Cyclic Modeling
- •7.2.1. The Basic Sector
- •7.2.2. Edge Component Pairs
- •7.2.2.1. CYCOPT Auto Detection Tolerance Adjustments for Difficult Cases
- •7.2.2.2. Identical vs. Dissimilar Edge Node Patterns
- •7.2.2.3. Unmatched Nodes on Edge-Component Pairs
- •7.2.2.4. Identifying Matching Node Pairs
- •7.2.3. Modeling Limitations
- •7.2.4. Model Verification (Preprocessing)
- •7.3. Solving a Cyclic Symmetry Analysis
- •7.3.1. Understanding the Solution Architecture
- •7.3.1.1. The Duplicate Sector
- •7.3.1.2. Coupling and Constraint Equations (CEs)
- •7.3.1.3. Non-Cyclically Symmetric Loading
- •7.3.1.3.1. Specifying Non-Cyclic Loading
- •7.3.1.3.2. Commands Affected by Non-Cyclic Loading
- •7.3.1.3.3. Plotting and Listing Non-Cyclic Boundary Conditions
- •7.3.1.3.4. Graphically Picking Non-Cyclic Boundary Conditions
- •7.3.2. Solving a Static Cyclic Symmetry Analysis
- •7.3.3. Solving a Modal Cyclic Symmetry Analysis
- •7.3.3.1. Understanding Harmonic Index and Nodal Diameter
- •7.3.3.2. Solving a Stress-Free Modal Analysis
- •7.3.3.3. Solving a Prestressed Modal Analysis
- •7.3.3.4. Solving a Large-Deflection Prestressed Modal Analysis
- •7.3.3.4.1. Solving a Large-Deflection Prestressed Modal Analysis with VT Accelerator
- •7.3.4. Solving a Linear Buckling Cyclic Symmetry Analysis
- •7.3.5. Solving a Harmonic Cyclic Symmetry Analysis
- •7.3.5.1. Solving a Full Harmonic Cyclic Symmetry Analysis
- •7.3.5.1.1. Solving a Prestressed Full Harmonic Cyclic Symmetry Analysis
- •7.3.5.2. Solving a Mode-Superposition Harmonic Cyclic Symmetry Analysis
- •7.3.5.2.1. Perform a Static Cyclic Symmetry Analysis to Obtain the Prestressed State
- •7.3.5.2.2. Perform a Linear Perturbation Modal Cyclic Symmetry Analysis
- •7.3.5.2.3. Restart the Modal Analysis to Create the Desired Load Vector from Element Loads
- •7.3.5.2.4. Obtain the Mode-Superposition Harmonic Cyclic Symmetry Solution
- •7.3.5.2.5. Review the Results
- •7.3.6. Solving a Magnetic Cyclic Symmetry Analysis
- •7.3.7. Database Considerations After Obtaining the Solution
- •7.3.8. Model Verification (Solution)
- •7.4. Postprocessing a Cyclic Symmetry Analysis
- •7.4.1. General Considerations
- •7.4.1.1. Using the /CYCEXPAND Command
- •7.4.1.1.1. /CYCEXPAND Limitations
- •7.4.1.2. Result Coordinate System
- •7.4.2. Modal Solution
- •7.4.2.1. Real and Imaginary Solution Components
- •7.4.2.2. Expanding the Cyclic Symmetry Solution
- •7.4.2.3. Applying a Traveling Wave Animation to the Cyclic Model
- •7.4.2.4. Phase Sweep of Repeated Eigenvector Shapes
- •7.4.3. Static, Buckling, and Full Harmonic Solutions
- •7.4.4. Mode-Superposition Harmonic Solution
- •7.5. Example Modal Cyclic Symmetry Analysis
- •7.5.1. Problem Description
- •7.5.2. Problem Specifications
- •7.5.3. Input File for the Analysis
- •7.5.4. Analysis Steps
- •7.6. Example Buckling Cyclic Symmetry Analysis
- •7.6.1. Problem Description
- •7.6.2. Problem Specifications
- •7.6.3. Input File for the Analysis
- •7.6.4. Analysis Steps
- •7.6.5. Solve For Critical Strut Temperature at Load Factor = 1.0
- •7.7. Example Harmonic Cyclic Symmetry Analysis
- •7.7.1. Problem Description
- •7.7.2. Problem Specifications
- •7.7.3. Input File for the Analysis
- •7.7.4. Analysis Steps
- •7.8. Example Magnetic Cyclic Symmetry Analysis
- •7.8.1. Problem Description
- •7.8.2. Problem Specifications
- •7.8.3. Input file for the Analysis
- •Chapter 8: Rotating Structure Analysis
- •8.1. Understanding Rotating Structure Dynamics
- •8.2. Using a Stationary Reference Frame
- •8.2.1. Campbell Diagram
- •8.2.2. Harmonic Analysis for Unbalance or General Rotating Asynchronous Forces
- •8.2.3. Orbits
- •8.3. Using a Rotating Reference Frame
- •8.4. Choosing the Appropriate Reference Frame Option
- •8.5. Example Campbell Diagram Analysis
- •8.5.1. Problem Description
- •8.5.2. Problem Specifications
- •8.5.3. Input for the Analysis
- •8.5.4. Analysis Steps
- •8.6. Example Coriolis Analysis
- •8.6.1. Problem Description
- •8.6.2. Problem Specifications
- •8.6.3. Input for the Analysis
- •8.6.4. Analysis Steps
- •8.7. Example Unbalance Harmonic Analysis
- •8.7.1. Problem Description
- •8.7.2. Problem Specifications
- •8.7.3. Input for the Analysis
- •8.7.4. Analysis Steps
- •Chapter 9: Submodeling
- •9.1. Understanding Submodeling
- •9.1.1. Nonlinear Submodeling
- •9.2. Using Submodeling
- •9.2.1. Create and Analyze the Coarse Model
- •9.2.2. Create the Submodel
- •9.2.3. Perform Cut-Boundary Interpolation
- •9.2.4. Analyze the Submodel
- •9.3. Example Submodeling Analysis Input
- •9.3.1. Submodeling Analysis Input: No Load-History Dependency
- •9.3.2. Submodeling Analysis Input: Load-History Dependency
- •9.4. Shell-to-Solid Submodels
- •9.5. Where to Find Examples
- •Chapter 10: Substructuring
- •10.1. Benefits of Substructuring
- •10.2. Using Substructuring
- •10.2.1. Step 1: Generation Pass (Creating the Superelement)
- •10.2.1.1. Building the Model
- •10.2.1.2. Applying Loads and Creating the Superelement Matrices
- •10.2.1.2.1. Applicable Loads in a Substructure Analysis
- •10.2.2. Step 2: Use Pass (Using the Superelement)
- •10.2.2.1. Clear the Database and Specify a New Jobname
- •10.2.2.2. Build the Model
- •10.2.2.3. Apply Loads and Obtain the Solution
- •10.2.3. Step 3: Expansion Pass (Expanding Results Within the Superelement)
- •10.3. Sample Analysis Input
- •10.4. Top-Down Substructuring
- •10.5. Automatically Generating Superelements
- •10.6. Nested Superelements
- •10.7. Prestressed Substructures
- •10.7.1. Static Analysis Prestress
- •10.7.2. Substructuring Analysis Prestress
- •10.8. Where to Find Examples
- •Chapter 11: Component Mode Synthesis
- •11.1. Understanding Component Mode Synthesis
- •11.1.1. CMS Methods Supported
- •11.1.2. Solvers Used in Component Mode Synthesis
- •11.2. Using Component Mode Synthesis
- •11.2.1. The CMS Generation Pass: Creating the Superelement
- •11.2.2. The CMS Use and Expansion Passes
- •11.2.3. Superelement Expansion in Transformed Locations
- •11.2.4. Plotting or Printing Mode Shapes
- •11.3. Example Component Mode Synthesis Analysis
- •11.3.1. Problem Description
- •11.3.2. Problem Specifications
- •11.3.3. Input for the Analysis: Fixed-Interface Method
- •11.3.4. Analysis Steps: Fixed-Interface Method
- •11.3.5. Input for the Analysis: Free-Interface Method
- •11.3.6. Analysis Steps: Free-Interface Method
- •11.3.7. Input for the Analysis: Residual-Flexible Free-Interface Method
- •11.3.8. Analysis Steps: Residual-Flexible Free-Interface Method
- •11.3.9. Example: Superelement Expansion in a Transformed Location
- •11.3.9.1. Analysis Steps: Superelement Expansion in a Transformed Location
- •11.3.10. Example: Reduce the Damping Matrix and Compare Full and CMS Results with RSTMAC
- •Chapter 12: Rigid-Body Dynamics and the ANSYS-ADAMS Interface
- •12.1. Understanding the ANSYS-ADAMS Interface
- •12.2. Building the Model
- •12.3. Modeling Interface Points
- •12.4. Exporting to ADAMS
- •12.4.1. Exporting to ADAMS via Batch Mode
- •12.4.2. Verifying the Results
- •12.5. Running the ADAMS Simulation
- •12.6. Transferring Loads from ADAMS
- •12.6.1. Transferring Loads on a Rigid Body
- •12.6.1.1. Exporting Loads in ADAMS
- •12.6.1.2. Importing Loads
- •12.6.1.3. Importing Loads via Commands
- •12.6.1.4. Reviewing the Results
- •12.6.2. Transferring the Loads of a Flexible Body
- •12.7. Methodology Behind the ANSYS-ADAMS Interface
- •12.7.1. The Modal Neutral File
- •12.7.2. Adding Weak Springs
- •12.8. Example Rigid-Body Dynamic Analysis
- •12.8.1. Problem Description
- •12.8.2. Problem Specifications
- •12.8.3. Command Input
- •Chapter 13: Element Birth and Death
- •13.1. Elements Supporting Birth and Death
- •13.2. Understanding Element Birth and Death
- •13.3. Element Birth and Death Usage Hints
- •13.3.1. Changing Material Properties
- •13.4. Using Birth and Death
- •13.4.1. Build the Model
- •13.4.2. Apply Loads and Obtain the Solution
- •13.4.2.1. Define the First Load Step
- •13.4.2.1.1. Sample Input for First Load Step
- •13.4.2.2. Define Subsequent Load Steps
- •13.4.2.2.1. Sample Input for Subsequent Load Steps
- •13.4.3. Review the Results
- •13.4.4. Use Analysis Results to Control Birth and Death
- •13.4.4.1. Sample Input for Deactivating Elements
- •13.5. Where to Find Examples
- •Chapter 14: User-Programmable Features and Nonstandard Uses
- •14.1. User-Programmable Features (UPFs)
- •14.1.1. Understanding UPFs
- •14.1.2. Types of UPFs Available
- •14.2. Nonstandard Uses of the ANSYS Program
- •14.2.1. What Are Nonstandard Uses?
- •14.2.2. Hints for Nonstandard Use of ANSYS
- •Chapter 15: State-Space Matrices Export
- •15.1. State-Space Matrices Based on Modal Analysis
- •15.1.1. Examples of SPMWRITE Command Usage
- •15.1.2. Example of Reduced Model Generation in ANSYS and Usage in Simplorer
- •15.1.2.1. Problem Description
- •15.1.2.2. Problem Specifications
- •15.1.2.3. Input File for the Analysis
- •Chapter 16: Soil-Pile-Structure Analysis
- •16.1. Soil-Pile-Structure Interaction Analysis
- •16.1.1. Automatic Pile Subdivision
- •16.1.2. Convergence Criteria
- •16.1.3. Soil Representation
- •16.1.4. Mudslides
- •16.1.5. Soil-Pile Interaction Results
- •16.1.5.1. Displacements and Reactions
- •16.1.5.2. Forces and Stresses
- •16.1.5.3. UNITY Check Data
- •16.2. Soil Data Definition and Examples
- •16.2.1. Soil Profile Data Definition
- •16.2.1.1. Mudline Position Definition
- •16.2.1.2. Common Factors for P-Y, T-Z Curves
- •16.2.1.3. Horizontal Soil Properties (P-Y)
- •16.2.1.3.1. P-Y curves defined explicitly
- •16.2.1.3.2. P-Y curves generated from given soil properties
- •16.2.1.4. Vertical Soil Properties (T-Z)
- •16.2.1.4.1. T-Z curves defined explicitly
- •16.2.1.4.2. T-Z curves generated from given soil properties
- •16.2.1.5. End Bearing Properties (ENDB)
- •16.2.1.5.1. ENDB curve defined explicitly
- •16.2.1.5.2. ENDB curves generated from given soil properties
- •16.2.1.6. Mudslide Definition
- •16.2.2. Soil Data File Examples
- •16.2.2.1. Example 1: Constant Linear Soil
- •16.2.2.2. Example 2: Non-Linear Soil
- •16.2.2.3. Example 3: Soil Properties Defined in 5 Layers
- •16.2.2.4. Example 4: Soil Properties Defined in 5 Layers with Mudslide
- •16.3. Performing a Soil-Pile Interaction Analysis
- •16.3.2. Mechanical APDL Component System Example
- •16.3.3. Static Structural Component System Example
- •16.4. Soil-Pile-Structure Results
- •16.5. References
- •Chapter 17: Coupling to External Aeroelastic Analysis of Wind Turbines
- •17.1. Sequential Coupled Wind Turbine Solution in Mechanical APDL
- •17.1.1. Procedure for a Sequentially Coupled Wind Turbine Analysis
- •17.1.2. Output from the OUTAERO Command
- •Chapter 18: Applying Ocean Loading from a Hydrodynamic Analysis
- •18.1. How Hydrodynamic Analysis Data Is Used
- •18.2. Hydrodynamic Load Transfer with Forward Speed
- •18.3. Hydrodynamic Data File Format
- •18.3.1. Comment (Optional)
- •18.3.2. General Model Data
- •18.3.3. Hydrodynamic Surface Geometry
- •18.3.4. Wave Periods
- •18.3.5. Wave Directions
- •18.3.6. Panel Pressures
- •18.3.7. Morison Element Hydrodynamic Definition
- •18.3.8. Morison Element Wave Kinematics Definition
- •18.3.9. RAO Definition
- •18.3.10. Mass Properties
- •18.4. Example Analysis Using Results from a Hydrodynamic Diffraction Analysis
- •Index
- •ОГЛАВЛЕНИЕ
- •ВВЕДЕНИЕ
- •1.1. Методология проектирования технологических объектов
- •1.2. Компьютерные технологии проектирования
- •1.3. Системы автоматизированного проектирования в технике
- •1.4. Системы инженерного анализа
- •2.2.1. Создание и сохранение чертежа
- •2.2.2. Изменение параметров чертежа
- •2.2.3. Заполнение основной надписи
- •2.2.4. Создание нового вида. Локальная система координат
- •2.2.5. Вычерчивание изображения прокладки
- •2.2.6. Простановка размеров
- •2.2.7. Ввод технических требований
- •2.2.8. Задание материала изделия
- •2.3. Сложные разрезы в чертеже детали «Основание»
- •2.3.1. Подготовка чертежа
- •Cохранить документ.
- •2.3.2. Черчение по сетке из вспомогательных линий
- •2.3.3. Изображение разрезов
- •2.4. Чертежи общего вида при проектировании
- •3.1. Интерфейс программы
- •3.2. Общее представление о трехмерном моделировании
- •3.3. Основные операции геометрического моделирования
- •3.3.1. Операция выдавливания
- •3.3.2. Операция вращения
- •3.3.3. Кинематическая операция
- •3.3.4. Построение тела по сечениям
- •3.4. Операции конструирования
- •3.4.1. Построение фасок и скруглений
- •3.4.2. Построение уклона
- •3.4.3. Сечение модели плоскостью
- •3.4.4. Сечение по эскизу
- •3.4.5. Создание моделей-сборок
- •3.5. Разработка электронных 3D-моделей тепловых устройств
- •3.5.1. Электронные модели в ЕСКД
- •3.5.2. Электронные «чертежи» в ЕСКД
- •3.5.4. Электронная модель сборочного изделия «Газовая горелка»
- •ГЛАВА 4. ИНЖЕНЕРНЫЙ АНАЛИЗ ГАЗОДИНАМИКИ И ТЕПЛООБМЕНА В ANSYS CFX
- •4.1. Область применения ANSYS CFX
- •4.2. Особенности вычислительного процесса в ANSYS CFX
- •4.3. Программы, используемые при расчетах в ANSYS CFX
- •4.4. Организация процесса вычислений в среде пакета Workbench
- •4.4.1. Графический интерфейс пользователя
- •5.1. Постановка теплофизических задач в ANSYS Multiphysics
- •5.2. Решение задач в пакете ANSYS Multiphysics
- •5.2.1. Графический интерфейс пользователя
- •5.2.2. Этапы препроцессорной подготовки решения
- •5.2.3. Этап получения решения и постпроцессорной обработки результатов
- •5.3.5. Нестационарный теплообмен. Нагрев пластины в печи с жидким теплоносителем
- •5.4.1. Температурные напряжения при нагреве
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК

vk.com/club152685050 | vk.com/id446425943
ГЛАВА 5. ИНЖЕНЕРНЫЙ АНАЛИЗ ТЕПЛООБМЕНА
ИТЕРМИЧЕСКОЙ ПРОЧНОСТИ В ANSYS Multiphysics
5.1.Постановка теплофизических задач в ANSYS Multiphysics
5.1.1. Основные уравнения и условия однозначности в анализе
теплофизических процессов металлургии Уравнение энергии
Уравнение выражает закон сохранения энергии для каждого
элементарного объема dv (параллелепипеда |
с размерами dx, dy, dz). В |
направлении оси x теплопроводностью |
подводится поток тепла |
Q ў= |
- |
l |
¶ t |
¶ y¶ z¶ t . |
|
||||
x |
|
|
¶ x |
|
|
|
|
|
Через |
противоположную |
грань |
уходит |
|
ўў |
¶ |
ж |
||
Q |
|
з |
t + |
||
x |
= - l |
|
з |
||
|
|
|
¶ x и |
||
¶ t |
|
ц |
|
dx |
ч |
|
¶ y¶ z¶ t . |
|
|
|
ч |
¶ x |
|
ч |
|
ш |
Остается в объеме
|
|
|
|
|
|
|
|
|
¶ |
2 |
t |
|
dQ |
|
= Q |
ў |
Q |
ўў |
l |
|
dxdydzd t . |
||||
|
|
|
|
|||||||||
x |
x |
- |
x |
= |
¶ x |
2 |
||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
Потоки
dQ = dQ |
x |
+ dQ |
|
|
dQ |
y |
, dQ |
z |
|
|
y |
+ dQ |
. |
z |
|
, находятся аналогично
dQ |
x |
|
, и определяется величина
В результате поступления тепла меняется теплосодержание объема,
dQ » |
c |
r |
Dt |
¶ x¶ y¶ z¶ t . |
|
||||
|
p |
|
d t |
|
|
|
|
|
Полная производная
Dt |
= |
¶ t |
+ w |
|
¶ t |
+ w |
|
¶ t |
+ w |
|
¶ t |
|
d t |
¶ t |
x |
¶ x |
y |
¶ y |
z |
¶ z |
|||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
связана с движущейся материей (субстанцией) и часто называется субстанциональной. Она показывает, что изменение теплосодержания является результатом изменения температуры объема среды и конвективного перемещения тепла. На основании изложенного записано уравнение
теплопроводности Фурье–Кирхгофа
|
¶ t |
|
¶ t |
|
¶ t |
|
¶ t |
ж 2 |
t |
|
¶ |
2 |
t |
|
¶ |
2 |
t |
ц |
|
||
|
|
|
|
з ¶ |
|
|
|
|
ч |
|
|||||||||||
|
|
+ wx |
|
+ w y |
|
+ wz |
|
= a з |
|
|
+ |
|
|
|
+ |
|
|
|
ч, |
(5.1) |
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|||||||||
|
¶ t |
|
¶ x |
|
¶ y |
|
¶ z |
з |
|
|
¶ y |
|
|
¶ z |
|
ч |
|
||||
|
|
|
|
и¶ x |
|
|
|
|
|
ш |
|
||||||||||
где wx, wy, wz – компоненты скорости движения среды; |
a = |
|
l |
– коэффициент |
|||||||||||||||||
|
|
||||||||||||||||||||
|
c p r |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
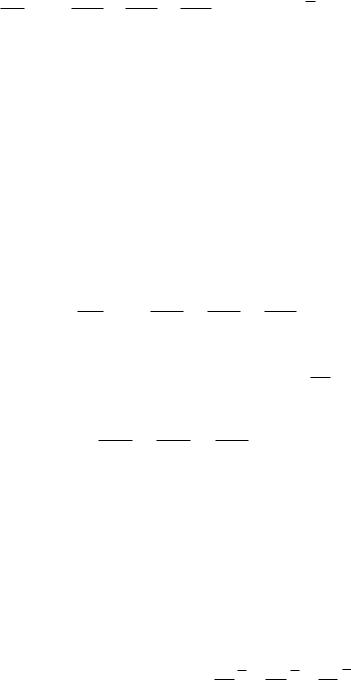
температуропроводности; λ – коэффициент теплопроводности; сР – удельная теплоемкость.
145
vk.com/club152685050 | vk.com/id446425943
При наличии тепловыделения в объеме (объемные химические реакции горения, работа трения и др.) и радиационного теплопереноса уравнение энергии имеет вид
|
D t |
|
|
ж |
2 |
t |
|
¶ |
2 |
t |
|
¶ |
2 |
t |
ц |
|
|
|
|
|
r c |
= |
l |
з |
¶ |
|
+ |
|
+ |
|
ч |
|
+ divq |
|
, |
||||||
|
з |
|
|
|
|
|
|
|
|
|
ч+ q |
v |
r |
|||||||
|
|
|
|
з |
|
|
2 |
|
|
|
2 |
|
|
|
2 |
ч |
|
|
||
|
d t |
|
|
и¶ x |
|
¶ y |
|
¶ z |
ч |
|
|
|||||||||
|
|
|
|
|
|
|
|
ш |
|
|
|
|
||||||||
где qv – интенсивность внутренних источников тепла, Вт/м3;
(5.2)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶ |
qr , x |
|
¶ |
qr , y |
|
¶ |
qr ,z |
|
|||||
|
|
|
|
|
|
|||||||||||
divqr |
= |
|
|
|
+ |
|
|
|
+ |
|
|
|
– дивергенция вектора излучения (поток вектора |
|||
¶ x |
¶ y |
¶ z |
||||||||||||||
|
|
|
|
|
|
|
||||||||||
через замкнутую поверхность объема, отнесенный к величине этого объема).
В расчетной практике большое значение имеют частные случаи уравнения энергии. У твердого тела wx= 0; wy= 0; wz= 0 и уравнение (5.1)
имеет вид
¶ t |
|
ж |
2 |
t |
|
¶ |
2 |
t |
|
¶ |
2 |
t |
ц |
|
= |
з |
¶ |
|
+ |
|
+ |
|
ч |
||||||
¶ t |
a з |
|
|
|
¶ y |
|
¶ z |
|
ч. |
|||||
|
з ¶ x |
2 |
|
2 |
|
2 |
ч |
|||||||
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
ш |
(5.3)
При стационарной теплопроводности с учетом
¶ |
2 |
t |
|
¶ |
2 |
t |
|
¶ |
2 |
t |
|
|
|
+ |
|
+ |
|
= 0. |
|||||||
¶ x |
2 |
¶ y |
2 |
¶ z |
2 |
|||||||
|
|
|
||||||||||
|
|
|
|
|
|
|||||||
¶ t |
= |
0 |
|
¶ t |
|||
|
|
получено
(5.4)
Это уравнение называют уравнением Лапласа. При стационарном процессе с внутренними источниками тепла уравнение энергии имеет вид
¶ 2t |
+ |
¶ 2t |
+ |
¶ 2t |
= - |
qv |
. |
(5.5) |
¶ x 2 |
¶ y 2 |
¶ z 2 |
|
|||||
|
|
|
l |
|
||||
Выражение (5.5) называют уравнением Пуассона.
Используя обозначения:
С = |
¶ |
i |
+ |
¶ |
j + |
¶ |
k |
|
¶ x |
¶ y |
¶ z |
||||||
|
|
|
|
|
–векторный
дифференциальный оператор набла (частично совпадает с оператором
146

vk.com/club152685050 | vk.com/id446425943
Гамильтона)8; и
уравнения (5.2)
i , j , k
– единичные векторы, получим векторную запись
¶ t |
+ wgradt = aС |
2 |
t + q |
+ |
divq |
|
|
|
|||||
|
|
r |
||||
¶ t |
|
|
V |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
где w – скорость жидкости.
(5.6)
Уравнение неразрывности (сплошности)
Вывод уравнения основан на законе сохранения массы для любого элементарного объема. По аналогии с выводом предыдущего раздела определяется поток массы жидкости, втекающей в объем в направлении оси
x, –
M ў= r w |
dydzd t |
|
x |
x |
|
. |
Масса, |
вытекающая |
из |
объема, |
– |
|
ўў |
|
|
¶ (r w |
) |
|
|
M |
|
+ |
x |
|
dx )dydzd t |
||
x |
= (r w |
x |
¶ x |
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
.
Изменение |
массы |
– |
ўў |
ў |
= |
¶ (r wx ) |
dxdydzd t |
. Изменение массы компенсируется |
|
|||||
dM x = M x - |
M x |
¶ x |
|||
|
|
|
|
|
изменением плотности объема во времени
dM |
|
+ dM |
|
+ dM |
|
= - |
¶ r |
dvd t |
|
x |
y |
z |
¶ t |
||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
.
8 |
Через оператор набла выражаются основные операции векторного анализа. |
||||||||||||||
|
|||||||||||||||
Например: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
градиент |
gradj = С j = |
¶ j |
i + |
¶ j |
j + |
¶ j |
k |
– вектор, показывающий |
|||||||
|
|
|
|
|
|
||||||||||
|
|
|
¶ x |
|
|
¶ y |
|
|
|
¶ z |
|
||||
направление наискорейшего роста некоторой скалярной |
функции φ от координат x, y, z |
||||||||||||||
(оператор набла умножен на скалярную величину); |
|
|
|
|
|
||||||||||
дивергенция |
divF = С ЧF = |
¶ Fx |
+ |
¶ Fy |
|
+ |
¶ Fz |
– дифференциальный оператор, |
|||||||
|
¶ y |
¶ z |
|||||||||||||
|
|
|
|
¶ x |
|
|
|
|
|||||||
отображающий векторное поле на скалярное (оператор набла умножен на векторную
величину). Физически, дивергенция отражает мощность источника или стока векторного
поля (div F>0 - в точке источник поля, |
div F<0 - в точке сток поля, div F=0 |
- источников |
|||||
нет, или они компенсируют друг друга). |
|
|
|
|
|||
Скалярное произведение |
С ЧС = С 2 = D называется оператором |
Лапласа. В |
|||||
декартовых координатах D = |
¶ 2 |
+ |
¶ 2 |
+ |
¶ 2 |
. |
|
¶ x 2 |
¶ y 2 |
¶ z 2 |
|
||||
|
|
|
|
|
|||
147
vk.com/club152685050 | vk.com/id446425943
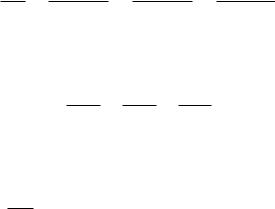
Отсюда после преобразований получено уравнение неразрывности
¶ r |
|
¶ (r w |
x |
) |
¶ (r w |
y |
) |
|
¶ (r w |
) |
|
|
+ |
|
|
+ |
|
+ |
z |
|
= 0 |
||
|
¶ x |
|
|
|
|
|
|
||||
¶ t |
|
|
|
¶ y |
|
|
|
¶ z |
|
|
Для несжимаемых жидкостей ρ = const
.
(5.7)
¶ w |
x |
¶ w |
y |
|
¶ w |
z |
|
|
+ |
+ |
|
= 0 |
|||
|
|
|
|
|
|||
¶ x |
¶ y |
|
|
¶ z |
|
|
|
В векторной форме уравнения (5.6) и (5.7) имеют
(5.8)
.
вид соответственно
¶ r |
+ div(r w) = 0 |
divw = |
0 |
(5.9) |
|
¶ t |
|||||
|
|
||||
|
и |
|
. |
||
|
|
|
Характер взаимосвязи величин, входящих в уравнение неразрывности,
хорошо иллюстрирует частный случай уравнения, записанный для «трубки тока». У трубки тока боковыми поверхностями являются «линии тока»,
касательные к которым совпадают с направлением скорости жидкости.
Частную запись уравнения неразрывности широко применяют в приближенных практических расчетах процессов и агрегатов на участках течений с постоянной массой, например в трубах или каналах. При этом для
двух произвольных сечений канала можно записать равенство |
|
|||||||||||
r |
1 |
w |
f |
1 |
= |
r |
2 |
w |
f |
2 |
|
(5.10) |
|
1 |
|
|
|
2 |
|
, |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
где ρ, w, f – плотность среды, скорость и площадь в сечении канала 1 или 2
соответственно. Из выражения (5.10) следует, что при постоянной плотности среды уменьшение площади поперечного сечения канала вдвое увеличит в два раза скорость потока.
Уравнения Навье–Стокса движения вязкой жидкости
На процесс движения жидкости большое влияние оказывают силы внутреннего трения. Свойство реальной жидкости оказывать сопротивление перемещению одной части жидкости относительно другой называется
вязкостью. Действие вязкости можно представить как перенос количеств движения молекулами, случайно перемещающимися из медленных слоев
жидкости в быстрые, и наоборот. Если «медленные» молекулы оказались среди
148

vk.com/club152685050 | vk.com/id446425943
быстрых, то они мешают общему движению, «тормозят» его. Между слоями появляется внутреннее трение (касательные напряжения).
Касательные напряжения трения в зависимости от градиента скорости определяет формула Ньютона
S |
|
= m |
¶ w |
x |
|
|
|
||||
xy |
¶ x |
||||
|
|
||||
|
|
|
|||
,
(5.11)
где μ – коэффициент динамической вязкости. Жидкости (вода, воздух и др.),
которые подчиняются закону (5.11) называются ньютоновскими.
Неньютоновскими жидкостями, например, являются растворы полимеров.
В физике сила, действующая на единицу поверхности, называется давлением (напряжением поверхностной силы). Внутренние силы – это силы взаимодействия отдельных частиц внутри объема. Внешние силы бывают массовые (объемные) – пропорциональны массе и равномерно распределены по объему (например, сила тяжести) и поверхностные – действуют на поверхности, ограничивающие объем (например, реакции стенок сосуда на жидкость). Поверхностные силы имеют составляющие: перпендикулярную поверхность (создают нормальное напряжение) и параллельную (создают касательное напряжение). Градиент скорости можно представить как относительный сдвиг соседних слоев жидкости – деформацию сдвига. Это означает, что выражение (5.12) устанавливает связь касательного напряжения в
жидкости со скоростью относительной деформации слоев.
Для вывода уравнений в потоке жидкости выделяется элементарный
объем с размерами ребер dx, dy dz. На объем действуют: сила тяжести, сила |
|
давления и сила трения. При выводе уравнения (из-за |
громоздкости вывод |
здесь не рассматривается) использован второй |
закон Ньютона: |
равнодействующая сил, |
действующих на элемент, равна произведению массы |
|||||
элемента на его ускорение. |
|
|
||||
Сила тяжести, |
приложенная |
к элементу, в проекции на |
ось x – |
|||
g x r ¶ x¶ y¶ z, |
где |
g |
– |
ускорение |
свободного падения. Силы |
давления, |
действующие |
на |
элемент в направлении, противоположном |
движению |
|||
|
|
|
|
|
149 |
|

vk.com/club152685050 | vk.com/id446425943
жидкости, –
-
¶p
¶x
dxdydz
. Силы трения направлены против движения
жидкости, но их равнодействующая определяется разностью сил трения на противоположных боковых гранях элемента. Для трехмерного движения она
равна
ж |
|
2 |
w |
|
|
¶ |
2 |
w |
|
|
|||
з |
¶ |
|
x |
+ |
|
x |
+ |
||||||
mз |
|
|
|
|
|
|
|
|
|
|
|
||
з |
|
¶ x |
2 |
|
|
¶ y |
2 |
|
|
||||
и |
|
|
|
|
|
|
|||||||
¶2 wx
¶z 2
ц ч чdxdydz ч ч ш
.
Здесь μ – коэффициент
динамической |
вязкости, wx |
– |
проекция скорости жидкости на ось x. |
В выражении |
учтено, что |
по |
закону Ньютона сила трения на единицу |
поверхности равна
записывается |
r |
Dw |
x |
|
|||
d t |
|
||
|
|
||
|
|
|
m |
¶ wx |
. Произведение массы элемента ρdυ на ускорение |
|
¶ x |
|||
|
|||
dv |
|
||
|
. |
|
|
В соответствии со сказанным уравнение Навье–Стокса принимает вид
|
¶ wx |
|
|
ж |
|
|
¶ wx |
|
|
|
¶ wx |
|
|
|
|
|
|
ц |
|
|
|
¶ p |
ж |
|
2 |
wx |
|
|
¶ |
|
2 |
wx |
|
|
|
¶ |
2 |
wx |
|
ц |
|
|||||||||||||||||||||||
|
|
|
зw |
|
|
|
|
|
|
|
|
¶ wx ч |
|
|
|
+ mз |
¶ |
|
|
|
|
|
|
|
|
|
|
ч |
|
|||||||||||||||||||||||||||||||||||
r |
|
|
|
+ r |
|
|
|
|
|
+ w |
|
|
|
|
+ w |
|
|
|
|
ч |
= r g - |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
ч, |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
з |
|
x |
|
|
|
|
y |
|
|
|
|
z |
|
|
|
ч |
|
x |
|
|
|
з |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
ч |
|
|||||||
|
|
¶ t |
|
|
з |
|
|
¶ x |
|
|
|
¶ y |
|
|
|
¶ z |
|
ш |
¶ x |
з |
|
¶ x |
|
|
|
|
¶ y |
|
|
|
|
|
|
¶ z |
|
|
ч |
|
||||||||||||||||||||||||||
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ш |
|
|||||||||||||||||||||||||
|
¶ wy |
|
|
ж |
|
|
¶ wy |
|
|
|
|
¶ wy |
|
|
|
|
¶ wy |
|
|
ц |
|
|
|
¶ p |
ж |
2 |
wy |
|
|
¶ |
|
2 |
w y |
|
|
¶ |
2 |
|
|
|
|
ц |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
з |
¶ |
|
|
|
|
|
|
|
|
w y ч |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ч |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ч |
(5.12) |
||||
r |
|
|
|
+ r |
w |
|
|
|
|
|
+ w |
|
|
|
|
+ w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ч= r g - |
|
|
|
+ mз |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
y |
|
|
|
|
z |
|
|
|
|
ч |
y |
|
|
|
з |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
ч |
|
||||||
|
|
¶ t |
|
|
з |
|
|
¶ x |
|
|
|
¶ y |
|
|
|
¶ z |
|
|
ш |
|
¶ y |
з |
|
|
|
|
|
|
|
|
|
|
¶ y |
|
|
|
|
|
|
|
¶ z |
|
|
ч |
|
|||||||||||||||||||
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и ¶ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ш |
|
||||||||||||||||||||||||
|
|
¶ wz |
|
|
ж |
|
|
|
¶ wz |
|
|
|
|
¶ wz |
|
|
|
|
|
|
ц |
|
|
|
¶ p |
ж |
|
2 |
wz |
|
|
¶ |
2 |
wz |
|
|
|
¶ |
2 |
wz |
ц |
|
||||||||||||||||||||||
|
|
|
+ r зw |
|
|
|
|
|
|
|
|
|
¶ wz ч |
|
|
|
+ mз |
|
¶ |
|
|
|
|
|
|
|
|
|
ч |
|
||||||||||||||||||||||||||||||||||
r |
|
|
|
|
|
|
|
+ w |
|
|
|
|
+ w |
|
|
|
|
ч |
= r g - |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
ч. |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
з |
|
|
x |
|
|
|
|
y |
|
|
|
|
z |
|
|
|
ч |
|
z |
|
|
|
з |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
ч |
|
||||||
|
|
¶ t |
|
|
з |
|
|
|
¶ x |
|
|
|
¶ y |
|
|
|
¶ z |
|
ш |
¶ z |
з |
|
¶ x |
|
|
|
¶ y |
|
|
|
|
|
|
|
¶ z |
|
ч |
|
||||||||||||||||||||||||||
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ш |
|
||||||||||||||||||||||||||||
Объединяя три уравнения в одно векторное уравнение, получим
r |
Dw |
= r g - |
С p + mС |
2 |
w |
|
|||||
d t |
|
||||
|
|
|
|
|
.
(5.13)
5.1.2. Задание граничных условий и параметров теплообмена в
ANSYS Multiphysics
Система дифференциальных уравнений имеет бесконечное множество решений. Выделить из них конкретное решение можно заданием условий однозначности (краевые условия). Это значит, нужно задать геометрические условия однозначности (задать форму и размеры объекта, в котором протекает процесс); физические условия однозначности (свойства среды и тел в объекте);
150

vk.com/club152685050 | vk.com/id446425943 |
|
|
|
|||
временные |
условия |
(обычно |
задаются |
начальные |
условия |
– |
температура в некоторый начальный момент времени τ0).
Особенности протекания процесса на границах тела задают граничные условия однозначности. Различают [8–10]:
Граничные условия I рода (условия Дирихле) – задаются распределения температуры по поверхности тела во времени T(x,y,z,τ) = φ(x,y,z,τ). Обычно условие используется для идеализированного описания реальных процессов в оценочных расчетах;
Граничные условия II рода (условия Неймана) – на границе задается плотность теплового потока как функция координат и времени
-
¶t
= (x, y, z, )
¶n
;
(5.14)
Граничные условия III рода – задается плотность теплового потока конвекции на границе как функция температуры поверхности тела tC и
температуры окружающей тело среды tЖ в виде
- |
|
¶ t |
= |
|
(t |
|
- |
t |
|
|
¶ n |
Ę |
C |
Ć |
|||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
)
,
(5.15)
где αК – коэффициент теплоотдачи, Вт/(м2·К).
Данное условие часто распространяют на процессы переноса тепла излучением. Для этого тепловой поток на стенку записывают в виде суммы потока тепла, переносимого конвекцией, и потока, переносимого излучением,
|
¶ t |
|
4 |
4 |
|
|
- |
|
= Ę (tC - tĆ )+ ĎĐ |
0 (TŃ - TĆ ) |
(5.16) |
||
¶ n |
||||||
|
||||||
|
|
|
|
, |
||
|
|
|
|
|
||
где εПР – приведенная степень черноты системы; 0=5,67·10-8 Вт/(м2·К4) –
постоянная Стефана–Больцмана. Отсюда получено выражение для коэффициента теплоотдачи излучением
Ę |
= |
|
Ď Đ |
0 (TC4 - TĆ4 |
) |
|
|
|
tC - tĆ |
|
(5.17) |
||
|
|
|
|
|||
|
|
|
|
|
; |
|
Граничные условия IV рода – задают условия на границе контакта двух
151

vk.com/club152685050 | vk.com/id446425943
сред с разными теплофизическими свойствами. Если на границе нет выделения или поглощения тепла, то обе среды имеют одинаковые температуры и тепловые потоки
- |
|
|
¶ t |
|
= |
- |
|
|
¶ t |
|
|
|
|
|
1 |
|
|
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
¶ n |
|
|
|
|
|
2 |
¶ n |
|
, |
|
|
|
|
Ń |
|
|
|
|
|
Ń |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
t |
|
= |
t |
2 |
|
. |
|
|
|
|
|
|
|
1 |
C |
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(5.18)
Если на границе идут процессы с выделением или поглощением тепла,
например, при фазовых превращениях, то в первое уравнение вводятся величины соответствующих потоков тепла. Для учета свойств в области теплового контакта вводятся дополнительные термические сопротивления.
Подробная информация о методах и особенностях вычислений содержится в разделе HELP программы и в литературе [11–14]. Геометрические условия однозначности в ANSYS задаются при твердотельном геометрическом моделировании объектов. Физические условия однозначности включают задание свойств (для этого есть специальная процедура) и внутренних источников тепла. Отдельно задаются конвективные и радиационные граничные условия третьего рода.
«Теплообменные» условия однозначности в ANSYS следующие.
1. Граничные условия I рода – задаются значения температуры (TEMP)
на поверхностях, линиях, узлах, ключевых точках (если они выделены при построении геометрической модели).
В одном из примеров следующего раздела задается температура 500 К
на линии границы (далее перечисляются опции, которые последовательно выбираются в окнах графического интерфейса):
MAIN MENU→SOLUTION→DEFINE LOADS→APPLY→ →THERMAL
→TEMPERATURE→ On Lines9
9 Здесь и далее показаны последовательности опций, выбираемых для задания
граничных условий в окнах меню или во всплывающих окнах программы
152
vk.com/club152685050 | vk.com/id446425943
Появляется меню «Apply TEMP». Щелчок курсором по верхней границе плиты, появляется штриховая линия →OK. Появилось второе меню «Apply TEMP on lines». Задать Lab2= TEMP; VALUE= 500 →OK. На поверхности появились треугольники, показывающие, что условия заданы.
2. Граничные условия II рода – задаются значения удельного теплового потока (HFLUX) на поверхностях, линиях, узлах, элементах (удельный тепловой поток через единицу поверхности q= –kA(dT/dx), где k – коэффициент теплопроводности; А – поверхность). Положительное значение потока означает, что элемент принимает тепло.
В одномерных моделях тепловой поток не задать, поэтому используют плотность теплового потока (HEAT– тепловой поток, протекающий через узел за единицу времени).
Конвективные граничные условия III рода – задается тепловой поток конвекцией (CONV) на внешней границе модели по закону Ньютона–Рихмана
q A h tS t f . Здесь
A h tS t f . Здесь
q 
A
– удельный тепловой поток конвекции через
поверхность A; h– коэффициент теплоотдачи конвекцией; tS, tf – температура поверхности и температура окружающей среды. В одном из примеров работы задан конвективный тепловой поток на поверхности (h=500, tf =500):
MAIN MENU → SOLUTION → DEFINE LOADS → APPLY → THERMAL → CONVECTION → On Lines Щелчок курсором по нижней границе плиты,
появляется штриховая линия → OK.
Появляется меню «Apply CONV on lines». В окна меню занести: SFL – constant value; VAL1. Film coefficient (коэффициент теплоотдачи) – 500; SFL – constant value; VAL2I. Bulk temperature (температура среды) – 500→OK.
Появляется предупреждение →Close. На верхней поверхности появилась
стрелка, значит условие задано;
3. Радиационные граничные условия III рода – задается тепловой поток
излучения на внешней границе модели по
qr A (T4 T04 ) ,
153
vk.com/club152685050 | vk.com/id446425943
где A – площадь поверхности; – степень черноты поверхности; – константа Стефана-Больцмана (5.67·10 - 8 Вт/(м2 · К)); Т – абсолютная температура тела;
T0 – абсолютная температура среды, окружающей поверхность.
Программа позволяет осуществить приближенную оценку радиационного теплообмена поверхностей и лучепрозрачной среды при использовании угловых коэффициентов. Точность таких оценок невелика.
Задание объемного энерговыделения HGEN – задается тепловыделение внутри элемента, вызванное или химической реакцией, или электрическим током, которое имеет размерность потока тепла, отнесенного к единице объема.
Используется последовательность операций MAIN MENU → SOLUTION →
DEFINE LOADS → APPLY → THERMAL → HEAT GENERAT.
Адиабатические условия – это частный случай граничного условия II
рода с заданным тепловым потоком на поверхности, который равен нулю.
Поверхность считается адиабатической по умолчанию, если на ней не заданы никакие граничные условия.
Условия симметрии рассматриваются как адиабатические.
Изложенное выше показывает, что в расчетах конвекции используется температура в первой степени, а в расчетах излучения – температура в четвертой степени. Расчеты облегчает функция сдвиг значения температуры,
позволяющая в радиационной задаче специальной командой задавать разность между абсолютным нулем и нулем используемой шкалы.
При расчетах в ANSYS должна контролироваться размерность вводимых величин. Информация, помогающая задавать расчетные параметры, содержится в табл. 5.1. В табл. 5.2 указаны форматы файлов, которые создаются ANSYS в
процессе вычислений.
154

vk.com/club152685050 | vk.com/id446425943
|
|
|
|
Таблица 5.1 |
|
Параметры, используемые в тепловом анализе |
|
||
|
|
|
|
|
|
Параметр |
Размерность |
|
Обозначение в |
|
|
|
|
ANSYS |
|
|
|
|
|
1 |
Температура |
К (°С) |
|
TEMP |
|
|
|
|
|
2 |
Координаты, длина |
м |
|
X,Y,Z |
|
|
|
|
|
3 |
Сила |
Н |
|
|
|
|
|
|
|
4 |
Время |
с |
|
TIME |
|
|
|
|
|
5 |
Масса |
кг |
|
|
|
|
|
|
|
6 |
Давление |
Па |
|
PRESSURE |
|
|
|
|
|
7 |
Давление, заданное на поверхность |
Па |
|
PRES |
|
|
|
|
|
8 |
Скорость |
м/с |
|
VELOCITY |
|
|
|
|
|
9 |
Ускорение |
м/с2 |
|
|
|
|
|
|
|
10 |
Плотность |
кг/м3 |
|
DENS |
|
|
|
|
|
11 |
Напряжение |
Па |
|
|
|
|
|
|
|
12 |
Модуль Юнга |
Па |
|
|
|
|
|
|
|
13 |
Мощность |
Вт |
|
|
|
|
|
|
|
14 |
Теплопроводность |
Вт/(м·К) |
|
KXX |
|
|
|
|
|
15 |
Плотность теплового потока |
Вт/м2 |
|
HFLUX |
|
|
|
|
|
16 |
Теплоемкость |
Дж/(кг·К) |
|
C |
|
|
|
|
|
17 |
Тепловой поток |
Вт |
|
HEAT |
|
|
|
|
|
18 |
Объемное энерговыделение |
Вт/м3 |
|
HGEN |
|
|
|
|
|
19 |
Коэффициент теплоотдачи конвекцией |
Вт/(м2 К) |
|
CONV |
|
|
|
|
|
20 |
Динамическая вязкость |
кг/(м ·с) |
|
μ |
|
|
|
|
|
21 |
Кинематическая вязкость |
м2/с |
|
|
|
|
|
|
|
22 |
Степень черноты |
- |
|
ε |
|
|
|
|
|
23 |
Расход жидкости |
|
|
FLOW |
|
|
|
|
|
24 |
Скорость (flotran) |
|
|
VELOCITY |
|
|
|
|
|
25 |
Тепловое излучение |
|
|
RAD |
|
|
|
|
|
155

vk.com/club152685050 | vk.com/id446425943
26 |
Температура жидкости вычисляемая |
|
|
TFLUID |
|
|
|
|
|
|
|
27 |
Температура поверхности элемента |
|
|
TS |
|
|
|
|
|
|
|
28 |
Плотности тепловых потоков в узлах |
|
|
TFX,TFY,TFZ |
|
|
|
|
|
|
|
29 |
Градиенты температуры в узлах |
|
|
TGX,TGY,TGZ |
|
|
|
|
|
|
|
30 |
Смещения по X и Y |
|
|
UX,UY |
|
|
|
|
|
|
|
31 |
Скорость по X,Y,Z |
|
|
VX,VY,VZ |
|
|
|
|
|
|
|
32 |
Относительное давление |
|
|
PREZ |
|
|
|
|
|
||
33 |
Кинетическая энергия турбулентности |
|
ENKE |
||
|
|
|
|
|
|
34 |
Коэффициент |
диссипации |
|
ENDS |
|
|
турбулентности |
|
|
|
|
|
|
|
|
||
35 |
Эффективная вязкость (с учетом |
|
EVIS |
||
|
турбулентн.) |
|
|
|
|
|
|
|
|
|
|
36 |
Эффективная |
теплопроводность |
(с |
|
ECON |
|
учетом турбулентности) |
|
|
|
|
|
|
|
|
|
|
37 |
Коэффициент турбулентной вязкости |
|
|
CMUV |
|
|
|
|
|
|
|
38 |
Плотность |
теплового потока |
на |
|
HFLU |
|
внешней поверхности |
|
|
|
|
|
|
|
|
||
39 |
Коэффициент теплоотдачи на внешней |
|
HFLM |
||
|
поверхности |
|
|
|
|
|
|
|
|
||
40 |
Плотность теплового потока излучения |
|
RDEL |
||
|
|
|
|
|
|
41 |
Площадь |
|
|
м2 |
A |
|
|
|
|
|
|
|
Таблица 5.2 |
Виды и форматы файлов, создаваемых ANSYS |
|
|
|
Назначение файла |
Формат имени файла |
|
|
Log файл для полной записи программы |
Jobname.log |
|
|
Файл базы данных |
Jobname.db |
|
|
Файл резервной базы данных |
Jobname.dbb |
|
|
Файл результатов термического анализа |
Jobname.rth |
|
|
Файл результатов гидродинамического анализа |
Jobname.rfl |
|
|
156
vk.com/club152685050 | vk.com/id446425943
Файл результатов конструкционного анализа |
Jobname.rst |
|
|
Файл результатов электромагнитного анализа |
Jobname.rmg |
|
|
Файл ошибок |
Jobname.err |
|
|
Файл вывода |
Jobname.out |
|
|
Файл пошаговой нагрузки |
Jobname.sn |
|
|
Файл графики |
Jobname.grph |
|
|
Файл матрицы элементов |
Jobname.emat |
|
|
Файл с элементами сетки |
Jobname.elm |
|
|
Файл с узлами сетки |
Jobname.nod |
|
|
Файл-библиотека с пользовательскими свойствами |
Jobname. SI_MPL |
материалов |
|
|
|
5.1.3. Модели турбулентности, используемые в программе ANSYS
Multiphysics
Модели с детальным описанием процессов
В расчетах турбулентности используются представления аналогии
Рейнольдса о существовании дополнительного турбулентного переноса тепла и количества движения. В соответствии с ними влияние турбулентности на
движение |
среды учитывается |
с помощью |
дополнительной (турбулентной) |
||
вязкости |
Т, возникающей в |
потоке |
m = m + m |
. Аналогично вязкости |
|
e |
T |
||||
определяется дополнительная (турбулентная) теплопроводность среды λТ,
учитывающая дополнительный перенос тепла вследствие турбулентности.
Связь между коэффициентами вязкости и теплопроводности в ламинарном потоке учитывает число Прандтля. При тепловом анализе обычно используют понятие о турбулентном числе Прандтля, которое устанавливает связь между турбулентными коэффициентами вязкости и теплопроводности
PrT = μT cP  λT [15,16]. Для многих течений жидкостей и газов считают
λT [15,16]. Для многих течений жидкостей и газов считают
PrТ≈0,9. На самом деле это значение справедливо для внутренней области пограничного слоя, оно снижается до 0,5 во внешней области и зависит от
геометрии потока. При заданном турбулентном числе Прандтля находят только
157

vk.com/club152685050 | vk.com/id446425943
один из коэффициентов (турбулентную вязкость), а турбулентную теплопроводность вычисляют через PrТ.
Относительно новыми подходами к моделированию турбулентных течений является [17-20] использование прямого численного моделирования
(DNS – Direct Numerical Simulation) и моделирования крупных вихрей (LES – Large Eddy Simulation). В DNS решаются полные нестационарные уравнения Навье–Стокса без использования каких-либо специальных моделей турбулентности, т.е. особенности течения учитываются без дополнительного моделирования. Решение требует настолько подробных сеток и малых шагов расчета по времени, для этого нужна настолько большая компьютерная память,
что в настоящее время расчеты могут быть реализованы только при малых числах Рейнольдса.
Большие вычислительные затраты необходимы и для полупрямых методов моделирования, например, для метода крупных вихрей (LES). В нем
«используются специальные фильтры для вывода уравнений разрешенных масштабов»10. Исключается из расчета мелкомасштабная турбулентность,
которая «слабее» и содержит меньше рейнольдсовских напряжений, чем крупномасштабная вихревая структура. «Главная проблема в моделировании крупных вихрей состоит в том, что вблизи стенки все вихри настолько малы,
что размеры энергоемких и диссипирующих вихрей совпадают. Это, конечно,
создает серьезные ограничения по числу Рейнольдса для LES». Для развития метода опробовано значительное число фильтров, граничных условий,
расчетных схем. Показано, что LES представляет собой перспективное направление в развитии методов расчета турбулентных течений.
На практике для описания трехмерных турбулентных течений часто используют осредненные по времени уравнения Навье–Стокса (RANS – Reynolds Averaged Navier–Stokes equation). При этом основной задачей
10 Фразы в кавычках приняты автором в терминологии описаний фирмы ANSYS или
рекламных материалов пакета программ
158

vk.com/club152685050 | vk.com/id446425943
становится определение коэффициента турбулентной вязкости. Величина Т
может сильно отличаться в разных точках пространства и зависеть от типа течения.
Модели турбулентности подразделяют по числу уравнений,
используемых в дополнение к уравнениям Навье–Стокса: модели «ноль уравнений» (алгебраические), «одного уравнения» (например, модель Спаларта–Аллмараса), «двух уравнений» (k- ε и k- модели).
Среди моделей турбулентности различают низкорейнольдсовские (LowReynolds) и высокорейнольдсовские (High-Reynolds). Это связано с тем, что модели с разной степенью адекватности учитывают процессы, происходящие в пристеночной области. Вблизи стенок силы инерции меньше сил вязкости
(локальное значение Re мало) и течение не полностью турбулентно.
Низкорейнольдсовские модели могут без привлечения дополнительных условий, но при наличии качественной сетки адекватно моделировать процессы вблизи стенок, а высокорейнольдсовские не могут.
Алгебраические модели
Используют алгебраические соотношения для связи турбулентной вязкости с осредненными величинами и геометрическими характеристиками.
Модели просты, их легко настроить на учет специфики рассматриваемых течений, они экономичны по вычислительным ресурсам. Но модели недостаточно полно отражают механизм процесса, и ожидать от них высокой точности результатов не следует.
Модель путисмешения Л. Прандтля
В модели считается, что характерный масштаб пульсаций скорости равен градиенту осредненной скорости, умноженному на характерный масштаб длины lm , который Прандтль назвал путем смешения. Выражение для кинематической турбулентной вязкости имеет вид
|
|
|
|
|
|
2 |
¶ |
u |
|
|
|
n T = lm |
|
|
|
. |
(5.19) |
¶ y |
|
||||
|
|
|
|||
|
|
|
|
||
159

vk.com/club152685050 | vk.com/id446425943
На основании эмпирических данных считается lm = ky, где k = 0,4-0,42 –
постоянная Кармана (известны более сложные зависимости lm(y), учитывающие влияние расстояния до стенки и других параметров [21]).
Модель работает при расчете сдвиговых слоев, но в иных случаях может требовать коррекции. Например, там, где градиент скорости равен нулю,
вязкость nT |
= 0 , что не соответствует действительности. |
Часто |
используется модель Прандтля, усовершенствованная Ван– |
Дристом [15]. В соответствии с ней:
n |
|
= |
2 |
f |
|
¶ u |
, |
T |
L |
V - D |
¶ y |
||||
|
|
|
|
|
|||
|
|
|
|
|
|
|
(5.20)
где L – масштаб турбулентности (длина пути смешения), рассчитывается по
одной из формул
|
|
2 |
3 |
|
L / d = 0, 4 y / d - |
0, 5( y / d) + 0, 2 |
( y / d) |
, č ëč |
|
|
й |
5 |
щ |
|
L / d = 0, 08 1- |
( y / d) |
; |
|
|
|
к |
|
ъ |
|
|
л |
|
ы |
|
(5.21)
|
|
|
й |
|
|
|
|
|
|
2 |
|
|
|
|
|
( |
|
|
|
щ |
|
||
f |
|
= |
1 - |
exp |
y |
|
/ A |
) |
|
|
|
V - D |
- |
+ |
ъ |
– поправочный множитель, распространяющий |
|||||||
|
|
к |
|
|
|
|
|||||
|
|
|
л |
|
|
|
|
|
ы |
|
|
модель пути смешения на вязкий подслой (А = 26 – постоянная Ван–Дриста;
y+ |
= |
yut |
/ n |
– безразмерная координата; ut = t w / r – динамическая |
скорость; |
t |
w |
– касательное напряжение по стенке); |
d |
– толщина |
|
|||||
|
|
гидродинамического пограничного слоя, в котором скорость меняется от нуля на стенке до значения скорости невозмущенного потока u0 (в практических расчетах границей пограничного слоя считают поверхность, в которой u=(0,99- 0,995) u0). Формулы для L учитывают, что у стенки масштаб турбулентности меняется линейно, а во внешней части пограничного слоя остается приблизительно постоянным.
Модель Денисова – Шкляра
Данная модель – одна из самых простых алгебраических моделей [22,23].
Она позволяет приближенно учесть турбулентность в задачах и программах, не
160

vk.com/club152685050 | vk.com/id446425943
поддерживающих специальных алгоритмов учета турбулентности. В ANSYS
модель может использоваться для оценочных вычислений наряду с более сложными моделями турбулентности.
Для расчетов поток газа условно разбивается на характерные зоны:
циркуляционную зону, зону настильного обтекания потоком стенки и др.
Считается, что в каждой из этих зон коэффициенты теплопроводности среды постоянны и равны некоторым эффективным величинам λЭФ, при которых результирующий конвективный теплообмен газа со стенками соответствует условиям турбулентного движения среды в канале. Для каждой характерной зоны записывается равенство
|
( |
|
- |
T |
) |
= |
|
Ý Ô |
( |
|
|
|
|
||||||||
T |
Ă |
|
|
T |
Ă |
|||||
|
|
|
ŃŇ |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
где ТГ – среднерасходная температура
- |
T |
|
ŃŇ |
газа в
) |
(5.22) |
,
зоне, прилегающей к стенке с
температурой ТСТ;
|
Ý Ô |
|
|
|
|
– термическая проводимость газа в зоне.
При ламинарном режиме движения среды λЭФ равен коэффициенту молекулярной теплопроводности λМ. Относительный коэффициент теплопроводности А при использовании чисел подобия Нуссельта Nu
Ŕ = |
Ý Ô |
= |
Nu |
(5.23) |
|
Ě |
NuË ŔĚ |
, |
|||
|
|
где NuЛАМ – число Нуссельта при ламинарном движении среды. Отношения чисел Нуссельта для каждой характерной зоны рассчитываются по формулам для ламинарного и турбулентного потоков в камере по средним значениям скорости потока в пределах зон. Более детальное описание процесса возможно при использовании локальных значений Nu, определенных по методу работы [24].
Значения турбулентных коэффициентов вязкости для решения газодинамической задачи определяют по турбулентному значению коэффициента теплопроводности, используя понятие о турбулентном числе Прандтля.
161
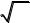
vk.com/club152685050 | vk.com/id446425943
Модель турбулентности ZEM (Zero Equation Model)
Простая модель турбулентной вязкости, использующая эмпирическую формулу
где
мп
п
LS = пн
пm
п
п
по
m |
2 |
Ô |
= r L |
||
T |
S |
|
|
LX , |
|
|
|
|
м |
0, 4 L |
|
|
ь |
|
п |
|
|
п |
|
|
п |
|
n |
п |
, |
|
in н |
|
|
|
э |
|
п0, 09 L |
|
п |
|
||
оп |
|
|
S юп |
||
,
ĺńëč LX > 0,
ĺńëč LX Ј 0,
(5.24)
(5.25)
ж |
|
|
|
|
ц |
¶ ui |
|
||
Ô = mз |
¶ ui |
|
¶ uk ч |
|
|||||
|
|
+ |
|
|
ч |
|
|
|
|
|
|
|
|
|
|
|
|||
з |
¶ x |
|
|
¶ x |
|
ч |
¶ x |
|
|
з |
|
|
|
ч |
|
– тензор вязкой диссипации; |
|||
и |
k |
|
|
i ш |
k |
||||
LX – масштаб длины; Ln – кратчайшее расстояние от узла до ближайшей границы; LS – характеристический масштаб длины (наибольшее значение Ln).
Модель имеет «небольшое физическое основание» и потому не рекомендуется для проведения точных расчетов.
Модели одного уравнения
Турбулентность описывается с помощью одной переменной, для которой составлено одно дифференциальное уравнение. Остальные характеристики турбулентности связываются с этой переменной при помощи алгебраических и иных уравнений.
Модель Спаларта – Аллмараса
Модель относится к числу низкорейнольдсовых. Она создавалась для задач внешней дозвуковой аэродинамики [25]. После введения ряда поправок модель «стала удовлетворительной» для многих инженерных приложений, в
частности, для течений в камерах с зонами циркуляции. Расчетные зависимости имеют вид:
n |
T |
= n%f |
V 1 |
|
|
– кинематическая турбулентная вязкость;
|
|
|
|
|
|
|
|
|
|
|
ж |
ц2 |
|
|
|
|
й |
|
|
щ |
|
|
|
|
|
|
|
|
¶ n% |
|
|
¶ n% |
|
|
% |
|
|
з |
n%ч |
|
1 d |
|
|
¶ n% |
cb 2 |
|
¶ n% ¶ n% |
(5.26) |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
+ u |
j |
|
|
= c |
b1 |
Sn%- c |
f |
W |
|
ч |
+ |
|
|
|
к n + n% |
|
ъ+ |
|
|
|
|
|
|
||||
|
|
|
|
|
|
W 1 |
|
з |
|
|
|
|
|
( |
) |
|
ъ |
|
|
|
|
|
|
|
||||
¶ t |
|
¶ x j |
|
|
|
|
|
|
ч |
|
|
|
|
к |
|
|
s ¶ xk ¶ xk |
|
||||||||||
|
|
|
|
|
|
иd ш |
|
s dxk л |
|
¶ xk ы |
|
|||||||||||||||||
162

vk.com/club152685050 | vk.com/id446425943
– уравнение турбулентной вязкости, где d – расстояние до ближайшей стенки.
|
c |
|
, c |
, s , c |
|
, f |
|
% |
|
|
|
Величины |
b1 |
|
W |
, S |
определяются |
из |
вспомогательных |
||||
|
b 2 |
W 1 |
|
|
|||||||
соотношений и коэффициентов замыкания. |
|
|
|||||||||
Модели |
|
с |
одним |
дифференциальным уравнением |
применимы для |
||||||
описания турбулентных течений с учетом сжимаемости, кривизны линий тока и отрыва потока. Однако используются они, как правило, для потоков с простой конфигурацией.
Модели двух уравнений
Наибольшее распространение получили k-ε и k- модели и их модификации. В k-ε моделях, которые дают неплохие результаты для подавляющего большинства турбулентных течений, эффективная вязкость Т
вычисляется как функция параметров турбулентности – кинетической энергии и скорости ее диссипации
|
|
|
k |
2 |
|
|
m |
= C |
r |
|
, |
|
|
|
|
(5.27) |
||||
T |
m |
|
e |
|
||
|
|
|
||||
|
|
|
|
|
||
где k – турбулентная кинетическая энергия; ε – турбулентная энергия диссипации. Двухпараметрические модели имеют общий недостаток: они считают турбулентную вязкость изотропной, что не всегда справедливо для сложных течений.
Встандартной модели k-ε и в модели RNG (Re-normalized Group Model)
–константа, в остальных моделях задается формулами. Для определения k и ε
должны быть решены два дополнительных уравнения.
Стандартная k-ε модель
Для стандартной k-ε модели дополнительные уравнения имеют вид:
уравнение турбулентной кинетической энергии
|
¶ k |
ж |
|
ц |
|
|
C |
b m |
|
|
|
|
||
|
з |
m |
ч |
|
|
|
|
|
|
|||||
r |
|
|
T |
T |
r e + |
4 |
|
T |
( |
g ЧС T |
) |
, |
||
|
з |
|
|
ч |
|
|
|
|||||||
|
+ r kС u = С Ч |
|
|
С k ч+ m Ô - |
|
|
|
|
|
|||||
|
¶ t |
з |
|
|
ч |
|
|
s |
|
|
|
|
|
|
|
иs |
k |
ш |
|
|
t |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
уравнение скорости диссипации
(5.28)
163

vk.com/club152685050 | vk.com/id446425943
|
|
ж |
|
ц |
|
|
|
|
|
|
|
2 |
C |
|
1- |
C |
|
) |
b r k |
|
|
||
|
¶ e |
|
m |
|
|
|
e |
|
|
|
e |
|
|
|
|
|
|||||||
|
+ r eС u = С з |
ч |
|
|
|
|
|
|
|
m |
( |
|
|
3 |
|
|
|
||||||
r |
|
|
T |
|
m |
|
Ô - |
C |
r |
|
|
+ |
|
|
|
|
|
( |
gС T . |
||||
|
|
С eч+ C |
1e |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
з |
|
|
ч |
T |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
) |
||
|
¶ t |
з |
|
|
ч |
|
|
k |
|
|
|
k |
|
|
|
s |
|
|
|
|
|
|
|
|
иs |
e |
ш |
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(5.29)
Значения коэффициентов в модели получены в результате подгонки результатов под экспериментальные данные и заданы в программе по умолчанию. Модель относится к числу высокорейнольдсовых.
Модель RNG (Renormalized Group Model)
RNG k-ε модель разработана на основе статистических методов. Она улучшает определение констант уравнения для ε. В результате величины становятся приемлемыми для низкорейнольдсных течений. Для этого, сохраняя расчетные выражения стандартной модели, величину С1ε определяют по
|
|
|
|
ж |
|
h |
|
ц |
|
|
|
|
|
з |
|
|
ч |
||
|
|
|
|
|
|
|
|
||
|
|
|
|
h 1- |
|
|
|
|
ч |
|
|
|
|
з |
|
|
|
|
ч |
|
|
|
|
з |
h |
|
|
ч |
|
C |
|
= 1, 42 |
|
и |
Ґ |
|
ш |
||
|
- |
|
|
|
|
. |
|||
1e |
1 + b |
|
h |
3 |
|||||
|
|
|
|
|
|||||
|
|
|
|
Ґ |
|
|
|||
|
|
|
|
|
|
|
|
|
|
(5.30)
Модели: NKE (New KE Model), GIR (Girimaji Model), SZL (Shih, Zhu,
Limley Model)
Данные модели представляют собой варианты k-ε модели, отличающиеся
способом определения коэффициентов.
Стандартная k- модель (Standard k-omega Model)
В модели турбулентности используется уравнение для турбулентной частоты вместо уравнения для диссипации энергии. Данное уравнение лучше описывает процесс около поверхности стенок. Поэтому в потоках с большими градиентами давлений более точно предсказывается масштаб турбулентности.
Модель низкорейнольдсовая. Выражение для турбулентной вязкости имеет вид
|
|
r k |
(5.31) |
|
mT |
= |
|
. |
|
|
|
|||
|
|
w |
|
|
Результаты моделирования у k- модели более точно соответствуют экспериментальным данным в пристеночной области, чем у k-ε модели. Однако расчеты для течений вне пограничного слоя могут давать результаты с
164
vk.com/club152685050 | vk.com/id446425943
большими погрешностями. Для корректного решения в пристеночных слоях нужна подробная сетка.
SST k- модель Ментера (shear-stress transport – перенос касательных напряжений).
Ментер объединил k-ε и k- модели турбулентности, используя k- – в
пристеночных областях, а k-ε – в области развитой турбулентности. Для этого уравнение k- модели умножили на функцию-переключатель моделей F1, а
сложенные с ними преобразованные для общего единообразия уравнения k-ε
модели на функцию (1-F1). Функция F1 равна единице вблизи стенки и нулю вдали от поверхности. Получилась низкорейнольдсовая модель, объединяющая достоинства двух моделей.
n |
2 |
-f |
|
модель турбулентности
В низкорейнольдсовой модели, сходной со стандартной k-ε моделью,
пытаются учесть неизотропные эффекты. Для этого добавлено уравнение для квадрата пульсаций поперечной скорости ν2 и специального релаксационного фактора f. Модель содержит четыре уравнения.
Среди прочих моделей отметим модель турбулентности Reynolds Stress, которую применяют при расчете потоков с сильной анизотропией и при расчете неравновесных эффектов. Решаемые уравнения модели сложны,
поэтому при их решении плохая сходимость. Модель турбулентности Eddy Viscosity предназначена для расчетов с незначительной турбулентностью,
которая непрерывно формируется и рассеивается.
Моделирование течений вблизи стенки
Низкорейнольдсовые модели способны моделировать процессы в пристеночных областях, но для этого им нужны качественные сетки и малый шаг расчета по времени. Высокорейнольдсовые модели могут использоваться в двухслойных моделях, как это сделано в SST k- модели Ментера. В работе
[26] используемая k-ε модель в пристеночной области была заменена моделью
165

vk.com/club152685050 | vk.com/id446425943
Прандтля с последующей «сшивкой» моделей. Такой подход может оказаться проблемным для использования в сложных течениях.
Обычно для моделирования течений высокорейнольдсовыми моделями используют метод пристеночных функций [25]. При этом расчет основной части потока проводится с использованием турбулентной модели, а расчет части потока, прилегающей к стенке, использует упрощенную методику. Пристеночная область течения разбивают на три (или больше [15]) характерные области.
1. В непосредственной близости от стенки выделяется вязкий подслой, в
котором вязкие напряжения доминируют над рейнольдсовыми, а тепло передается теплопроводностью. Следовательно, можно пренебречь турбулентной теплопроводностью λТ и турбулентной вязкостью Т. Скорость
потока линейно зависит от расстояния от стенки:
u |
+ |
= |
y |
+ |
, |
|
|
где
u |
+ |
= |
u |
|
|
|
|||
|
u |
|
||
|
|
|
T |
|
|
|
|
|
|
–
безразмерная скорость;
y |
+ |
= |
u |
T |
y |
|
|
||||
|
|
n |
|
||
|
|
|
|
|
– безразмерное расстояние от стенки;
u |
|
= |
s |
W |
|
|
|
||||
T |
r |
||||
|
|
||||
|
|
|
|||
– динамическая скорость.
2. Промежуточный слой, в котором вязкие и рейнольдсовы напряжения соизмеримы по величине. «Сшивая» распределения скорости в слое 1 и
следующем слое 3, получили распределение
u |
+ |
= 5ln y |
+ |
+ 3, 05. |
|
|
(5.32)
3. Логарифмический слой, в котором рейнольдсовы напряжения намного больше вязких. Здесь можно пренебречь молекулярным переносом тепла и импульса; распределение скорости подчиняется логарифмическому закону
+ |
1 |
( |
+ |
) |
(5.33) |
u = |
|
ln Ey |
|
, |
k
где k – постоянная Кармана; E – постоянная, определяющая степень шероховатости (для гладкой стенки экспериментально получено E=8,8).
Область, описываемая пристеночными функциями, занимает около 20 %
толщины пограничного слоя. В пристеночной области профиль скорости слабо
166
