Эффект Доплера
Пусть
в начале координат системы
находится излучатель (см. рис. 2). В начале
координат системы
‑ приемник.
Уравнение колебаний в системе имеет вид:
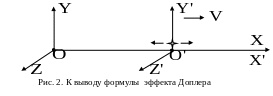
где
знак «‑» берется потому, что волна
распространяется в отрицательном
направлении оси
.
Уравнение колебаний в системе
(15)
Поскольку верен принцип относительности и все законы природы (в частности закон распространения электромагнитных волн) имеют одинаковый вид в любых инерциальных системах отсчета.
Но
в системе
уравнение колебаний можно получить,
исходя из уравнения колебаний в системе
,
путем замены
на
и
на
:
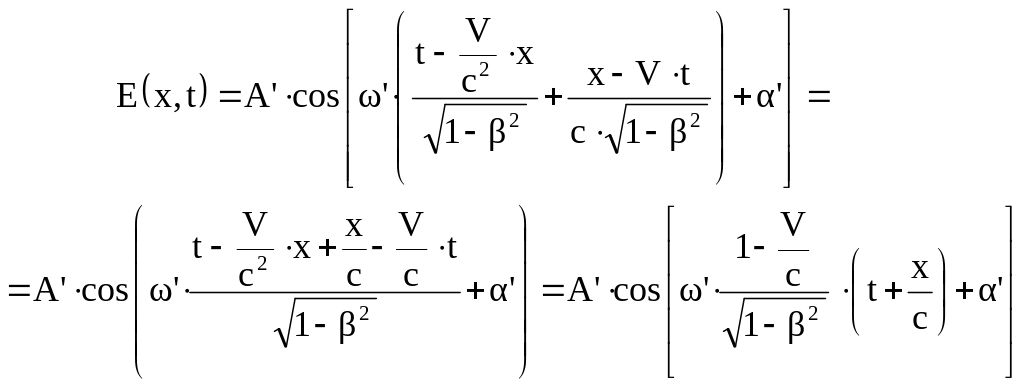
Сравнивая последнее уравнение с уравнением В, получим:
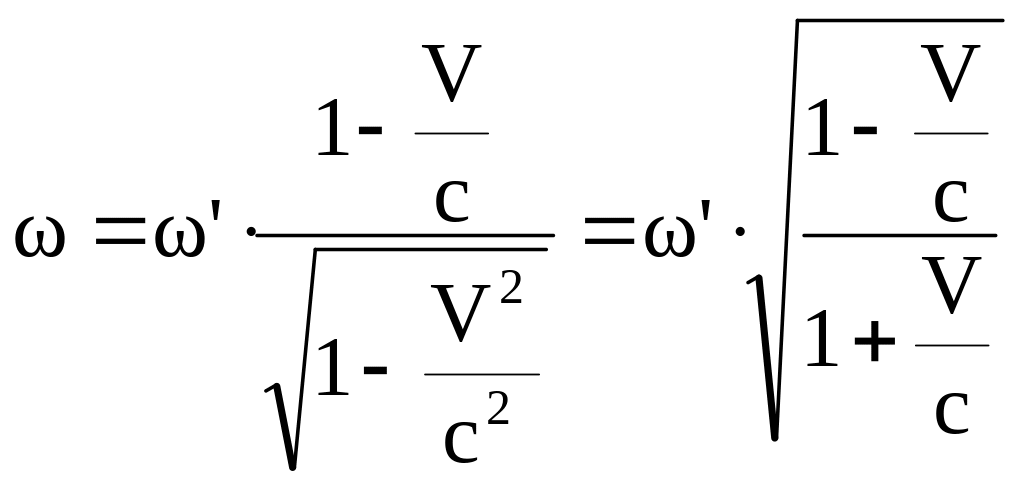
Переходя к линейной частоте, получим:
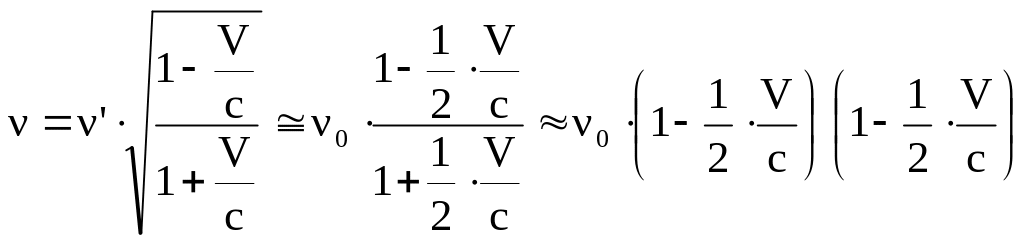
Или,
окончательно, при
(16)
Отсюда, относительное изменение частоты:
Это мы будем наблюдать, так называемый продольный эффект. Но кроме того будет наблюдаться и поперечный эффект Доплера, который в акустике не наблюдается. Однако тут формула для изменения частоты другая:
Поперечный эффект Доплера обусловлен изменением течения времени в различных инерциальных системах отсчета.
Эффект Доплера может быть использован для определения радиальной скорости звезд.
Наличием эффекта Доплера объясняется уширение спектральных линий вследствие теплового движения излучающих атомов и молекул.
В частности, с помощью эффекта Доплера были измерены радиальные скорости видимых Галактик. Оказалось, что все Галактики удаляются от нас со скоростью . Причем, чем дальше от нас находится Галактика, тем больше скорость , так, что выполняется соотношение:
Значение этой константы определено эмпирически.
Величину
,
имеющую размерность времени, называют
возрастом Вселенной:
Величину
,
имеющую размерность длины, называют
радиусом Вселенной:
Точный смысл этих величин, однако, до сих пор не ясен.
Лекция 5. (2 часа)
Свободные незатухающие и затухающие электромагнитные колебания
(Колебательный контур. Процессы в идеализированном колебательном контуре. Уравнение свободных незатухающих электромагнитных колебаний. Формула Томсона. Закон сохранения и превращения энергии в идеализированном колебательном контуре. Затухающие электромагнитные колебания в реальном колебательном контуре. Логарифмический декремент затухания и добротность колебательного контура.)
Свободные электрические колебания
в контуре без активного сопротивления
При
рассмотрении электрических колебаний
приходится иметь дело с токами,
изменяющимися со временем. Закон Ома и
вытекающие из него правила Кирхгофа
были установлены для постоянного тока.
Однако они остаются справедливыми и
для мгновенных значений изменяющихся
тока и напряжения, если их изменения
происходят не слишком быстро.
Электромагнитные возмущения
распространяются по цепи с огромной
скоростью, равной скорости света. Если
– длина цепи, то на прохождение её
электромагнитное возмущение затрачивает
время
,
где
- скорость света в вакууме.
Ток
называется квазистационарным,
когда мгновенные значения тока оказываются
практически одинаковыми на всех участках
цепи. Для периодически изменяющихся
токов условие квазистационарности
будет выполнено, если
где
- период изменений.
Например,
для цепи длиной
время
,
поэтому токи можно считать квазистационарными
вплоть до частот
(это соответствует
).
Мы будем рассматривать только квазистационарные токи при изучении всех видов электрических колебаний. Мгновенные значения квазистационарных токов подчиняются закону Ома. Следовательно, для них справедливы и правила Кирхгофа.
В
цепи, содержащей катушку индуктивностью
и конденсатор ёмкостью
,
могут возникать электрические колебания.
Поэтому такую цепь называют колебательным
контуром. Выясним,
каким образом в колебательном контуре
возникают и поддерживаются электрические
колебания.
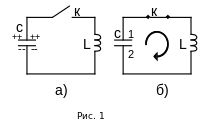
Пусть
вначале верхняя обкладка конденсатора
заряжена положительно, а нижняя
отрицательно (рис. 1,а). При этом вся
энергия колебательного контура
сосредоточена в конденсаторе. Замкнем
ключ
.
Конденсатор начнет разряжаться, и через
катушку
потечет ток. Электрическая энергия
конденсатора начнет превращаться в
магнитную энергию катушки. Этот процесс
закончится, когда конденсатор полностью
разрядиться, а ток в цепи достигнет
максимума (рис.1,б). С этого момента ток,
не меняя направления, начнет убывать.
Однако он прекратится не сразу – его
будет поддерживать э.д.с. самоиндукции
(
).
Ток будет перезаряжать конденсатор,
возникает электрическое поле, стремящееся
ослабить ток. Наконец ток прекратился,
а заряд на конденсаторе достигнет
максимума. С этого момента конденсатор
начнет разряжаться опять, ток потечет
в обратном направлении и т.д. - процесс
будет повторяться.
В контуре при отсутствии сопротивления проводников совершаются строго периодические колебания. В ходе процесса периодически изменяются заряд на обкладках конденсатора, напряжение на нём и ток через катушку. Колебания сопровождаются взаимными превращениями энергии электрического и магнитного полей.
Найдем уравнение колебаний в контуре без активного сопротивления. Прежде всего, выберем положительное направление обхода контура, например, по часовой стрелке, т.е. условимся считать положительным ток, заряжающий конденсатор. Тогда
. (1)
Напишем для колебательного контура выражение закона Ома:
. (2)
В
нашем случае
.
Подставив эти значения в (59), получаем:
. (3)
Учитывая,
что
,
получаем уравнение
. (4)
Уравнение (4) является дифференциальным уравнением гармонических колебаний. Из этого сравнения находим собственную частоту колебаний в контуре:
, (5)
а уравнение (61) принимает вид:
(6)
Решением этого уравнения является гармоническая функция
. (7)
Для периода собственных колебаний получается так называемая формула Томсона:
.
(8)
Напряжение на конденсаторе равно
(9)
Продифференцировав функцию (64), получим выражение для силы тока:
. (10)
Таким
образом, сила тока опережает по фазе
напряжение на конденсаторе на
.
В момент, когда ток достигает наибольшего значения, заряд и напряжение на конденсаторе обращаются в нуль, и наоборот. Из формул (9) и (7) следует, что
,
Взяв отношение этих амплитуд, получаем
(11)
Эту формулу можно получить, исходя из того, что наибольшее значение энергии электрического поля должно быть равно наибольшему значению магнитного поля, т.е.
.