Резонансные явления в колебательном контуре. Резонанс напряжений и резонанс токов.
Как следует из приведенных формул, при частоте переменной ЭДС ω, равной
,
амплитудное
значение силы
тока в
колебательном контуре, принимает
максимальное
значение
.
При этом амплитуда
напряжения
на активном
сопротивлении
R
также максимальна
и равна UR0
=I0maxR
=E0.
Падения
напряжения
на емкости UC
и индуктивности UL
одинаковы
по амплитуде, но противоположны
по фазе, и они взаимно компенсируют
друг друга. Это явление, имеющее место
в последовательном
колебательном
контуре,
изображенном на рис.1, называется
резонансом
напряжений.
Векторная диаграмма, соответствующая
этому случаю, показана на рис.4.
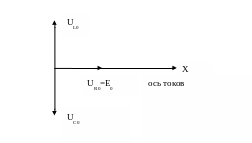
Рис.4. Векторная диаграмма при резонансе напряжений.
Максимальное значение амплитуды напряжения на конденсаторе UC0(ω) достигается при частоте
.
Резонансные кривые для UC0(ω) представлены на рис.16.8. Максимум получается тем выше и острее, чем меньше коэффициент затухания β, то есть чем меньше активное сопротивление R и больше индуктивность контура L.
UC0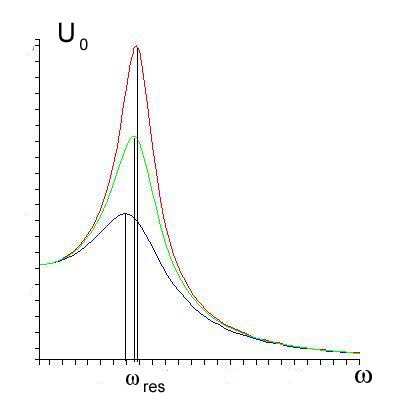
E0
ωрез
ω0
ω
Рис.5. Резонансные кривые UC0(ω).
Если источник переменной ЭДС подключить параллельно конденсатору, то получим колебательный контур, который называется параллельным (рис.6).
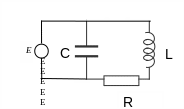
Рис.6. Параллельный колебательный RLC-контур.
В
таком контуре при
наблюдается другое резонансное явление,
получившее название резонанса
токов.
При резонансе токов токи,
текущие через емкость и индуктивность
одинаковы
по амплитуде, но противоположны
по фазе. При этом общий
ток
в цепи ЭДС близок
к нулю,
хотя токи
в самом контуре могут быть очень
велики.
Векторная диаграмма, соответствующая
этому случаю, приведена на рис.7.
Рис.7. Векторная диаграмма при резонансе токов.
Можно
показать, что при резонансе токов полное
сопротивление Z(ω)
параллельного контура максимально и
равно чисто активному
сопротивлению
R.
Резонансная частота, при которой Z(ω)
максимально, определяется из условия
равенства нулю реактивной части
комплексного сопротивления
:
ωL(1 – ω2LC) – ωCR2 = 0 ,
откуда
.
Резонансные кривые для амплитудных значений IC0(ω) тока, текущего через конденсатор, приведены на рис.8.
ω
IC0
ωрез
ω0
Рис.8. Резонансные кривые IC0(ω).
Резонансные явления в колебательных контурах широко используются в электро- и радиотехнике (резонансные усилители, частотные фильтры и другие). В частности, явление резонанса используется для выделения из сложного сигнала нужной частотной составляющей. Настроив контур (путем изменения его параметров C и/или L) на одну из выбранных частот, можно получить на конденсаторе напряжение, в Q раз превышающее величину напряжения данной частотной составляющей (см. рис.16.8). Такой процесс осуществляется, например, при настройке радиоприемника на нужную длину волны.
Электромагнитные волны.
Уравнения Максвелла устанавливают связь между электрическим и магнитным полями. Они показывают, что электрические и магнитные поля взаимосвязаны. Невозможно найти одно поле, не находя другого (исключая частный случай статических полей ‑ электростатика, магнитостатика).
Т.е. уравнения Максвелла говорят о существовании единого электромагнитного поля.
Дифференциальное уравнение плоской электромагнитной волны
Чтобы не прибегать к сложным математическим выкладкам, рассмотрим электромагнитное поле в диэлектрической среде. Пусть это поле имеет следующие компоненты:
Т.е.
электрическое поле имеет компоненты
‑
,
магнитное поле имеет компоненты ‑
.
Т.к.
среда ‑ диэлектрик, то токов
проводимости нет ‑
.
Кроме того, будем считать, что свойства
среды не меняются с течением времени,
т.е.
.
В этом случае первое уравнение Максвелла в дифференциальной форме будет иметь вид:
Операция ротора раскрывается как:
У
электрического поля есть компонента
только по оси
.
Поэтому уравнения Максвелла примет
вид:
Отсюда
вытекает ‑
.
Магнитное поле однородно вдоль оси
.
Таким образом, от этого уравнения Максвелла у нас осталось следующее уравнение:
Далее, рассмотрим второе уравнение Максвелла в дифференциальной форме:
Аналогичным образом раскроем операцию ротора:
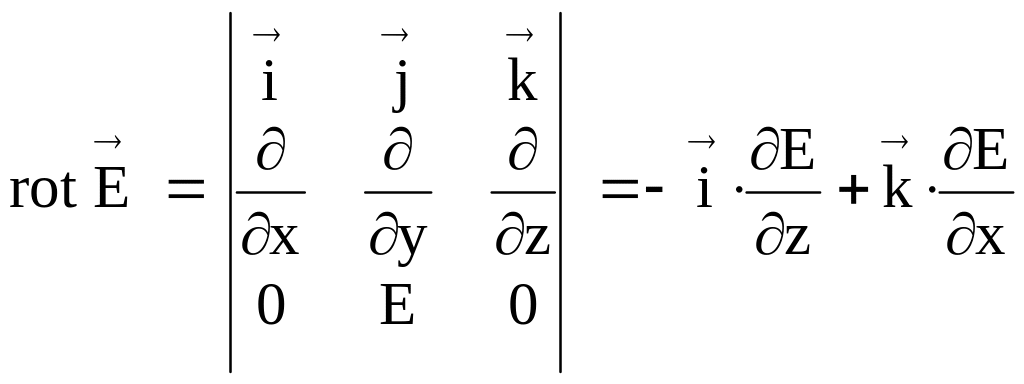
У
магнитного поля есть только одна
компонента по оси
,
поэтому:
Здесь
мы тоже полагаем, что магнитные свойства
среды не меняются с течением времени
‑
.
Отсюда вытекает, что электрическое
поле не меняется вдоль оси
‑
.
Т.е. свойства электромагнитного поля
не меняются в плоскости
,
поэтому такое поле называется плоским.
Таким образом, от второго уравнения Максвелла у нас осталось следующее уравнение:
Следовательно, для нахождения двух неизвестных компонент электромагнитного поля мы получили систему двух уравнений:
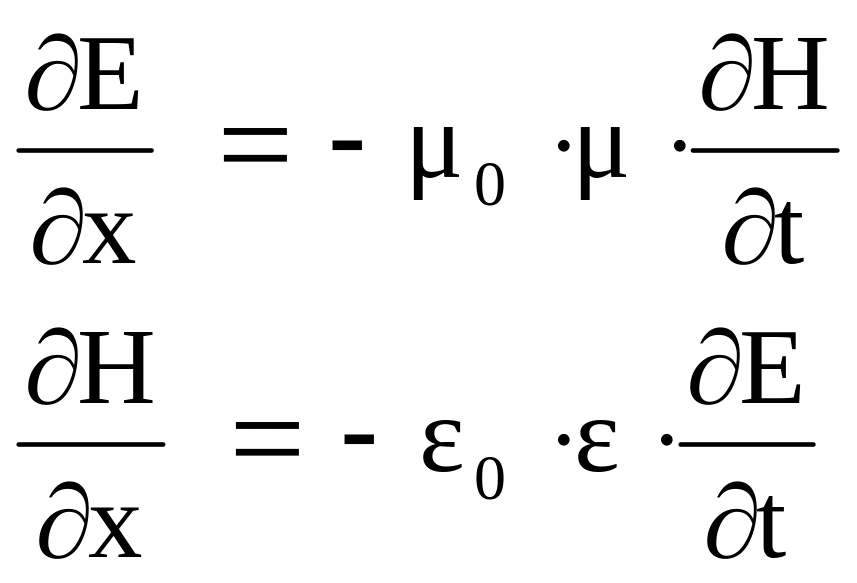
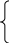(А)
Уравнение плоской электромагнитной волны
Разрешим полученную систему, например, относительно компоненты электрического поля . Для этого первое уравнение системы (А) продифференцируем по координате , а второе ‑ по времени :
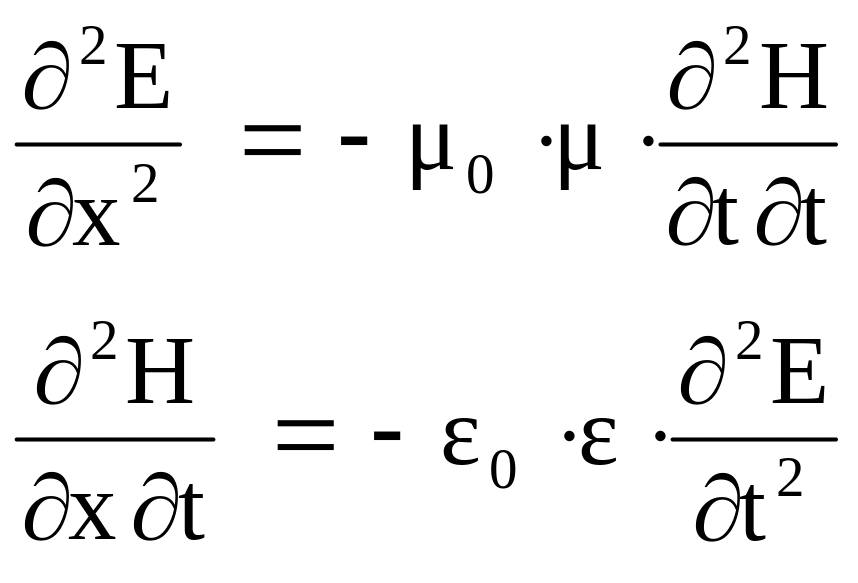
Отсюда,
исключая
,
получим:
(В)
Таким образом, мы получили дифференциальное уравнение второго порядка для нахождения компоненты вектора напряженности электрического поля.
Аналогичным же образом можно получить и второе уравнение для нахождения компоненты вектора напряженности магнитного поля:
(С)
Решение уравнений (В) и (C) имеет вид:
(D)
Т.е. мы видим, что решение представляет собой плоскую волну, распространяющуюся вдоль положительного направления оси .