Затухающие электрические колебания

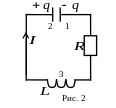
Каждый реальный колебательный контур обладает активным сопротивлением, и энергия, запасённая в контуре, постепенно расходуется на нагревание и излучение. Свободные колебания будут затухающими. Выражение закона Ома, написанное для цепи 1-3-2, изображенной на рис.2, имеет вид:

(12)

Разделив это уравнение на и учтя, , получим:

. (13)

Приняв во внимание, что , и введя обозначение , уравнению (70) можно придать следующий вид:

. (14)

Последнее уравнение совпадает с дифференциальным уравнением затухающих колебаний (32).

При условии, что решение уравнения (15) имеет вид:

, (16)

где

. (17)

Таким образом, частота затухающих колебаний меньше собственной частоты .

Величину называют периодом затухающих колебаний, несмотря на то, что функция (72) не периодическая.

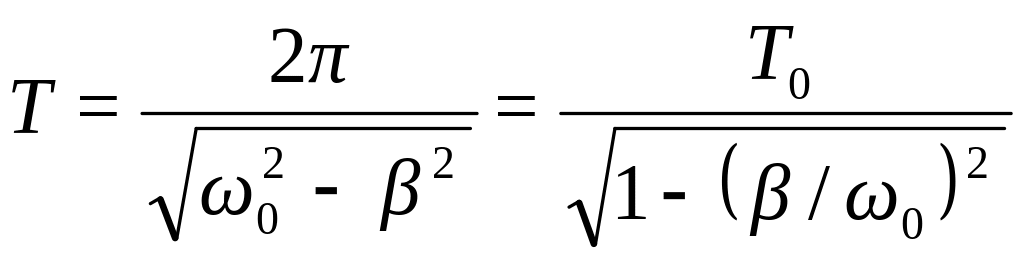, (18)

где - период свободных незатухающих колебаний. Период затухающих колебаний больше периода собственных незатухающих колебаний. Зная зависимость можно найти напряжение на конденсаторе и ток в контуре:

(19)

.

Умножив правую часть этой формулы на равное единице выражение , получим

.

Введя угол , определяемый условиями

, ,

можно написать

. (20).

П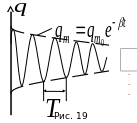 оскольку а значение заключено в пределах до . Таким образом, при наличии в контуре активного сопротивления сила тока опережает по фазе напряжение на конденсаторе более чем на (при опережение составляет ).

График функции (72) изображен на рис.19. Графики для напряжения и силы тока имеют аналогичный вид.

Затухание колебаний характеризуется рядом величин, рассмотренных нами при анализе затухающих механических колебаний (коэффициент затухания , время релаксации , логарифмический декремент затухания , добротность ). Если затухание мало ( ), то и. тогда

, (21)

. (22)

Есть ещё одна полезная формула для добротности в случае слабого затухания:

. (23)

где – энергия, запасенная в контуре, – уменьшение этой энергии за период .

В самом деле, энергия пропорциональна квадрату амплитуды заряда конденсатора, т.е. . Отсюда относительное уменьшение энергии за период . Учитывая, что , получаем формулу (79).

В заключение отметим, что при вместо колебаний будет происходить апериодический разряд конденсатора. Активное сопротивление контура, при котором наступает апериодический процесс, называется критическим:

. (24)

Лекция 6. (2 часа) Вынужденные электромагнитные колебания. Электромагнитные волны

(Вынужденные электромагнитные колебания. Электрический резонанс.

Возникновение электромагнитных волн. Уравнение плоской электромагнитной волны. Энергия электромагнитной волны. Шкала электромагнитных волн. Применение электромагнитных волн.)

Вынужденные электрические колебания

Вынужденные колебания в контуре можно осуществить, например, если последовательно в контур (см. рис. 1 а) подать переменное напряжение :

, (1)

где - амплитудное значение напряжения; - частота источника переменного напряжения.

Рис. 1 Схема для получения вынужденных колебаний в контуре

Это напряжение нужно прибавить к ЭДС самоиндукции и формула (9.2) примет вид:

,

или после подставки значений , и получим:

(2)

После преобразования, получим:

(3)

Решение этого уравнения имеет вид:

, (4)

где ; (5)

Подстановка значений и в формулы (5) даёт:

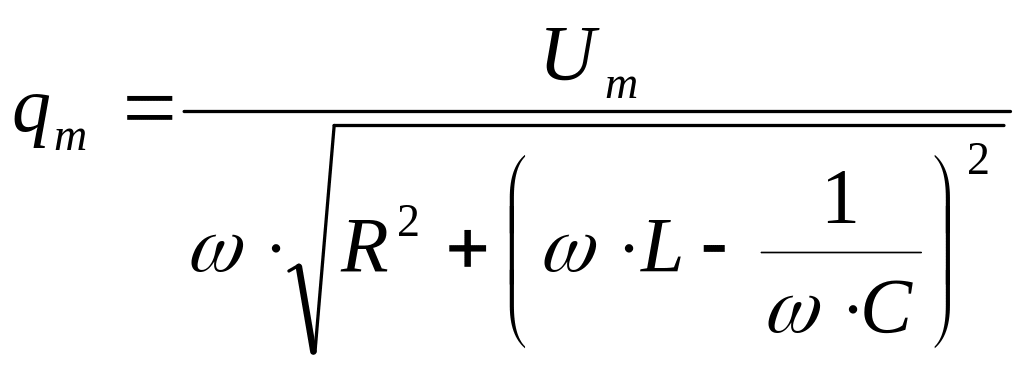(6)

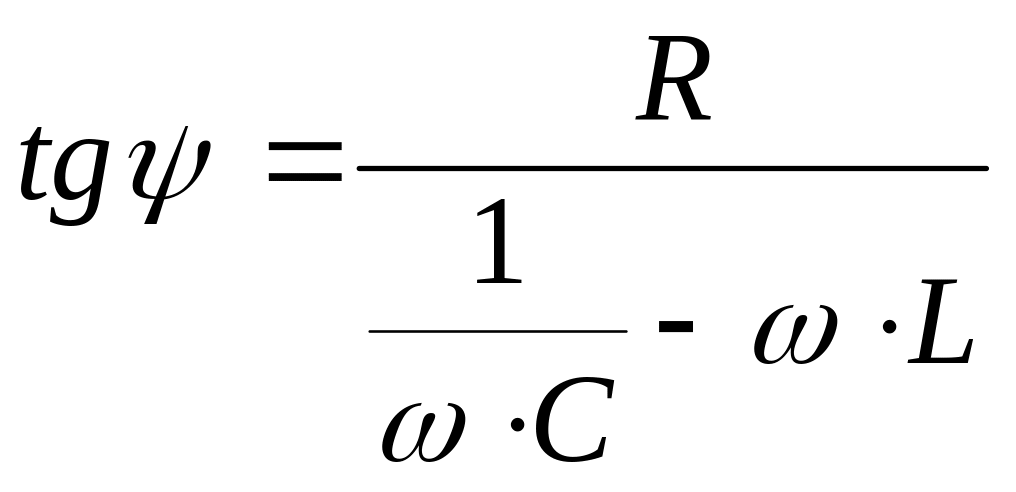(7)

Продифференцировав выражение (6) по t, найдём силу тока в контуре при установившихся колебаниях:

. Запишем это выражение в виде:

(8)

где есть разность фаз между током и приложенным напряжением . В соответствии с (7)

(9)

Из этой формулы следует, что ток отстаёт по фазе от напряжения (φ>0) в том случае, когда > , и опережает напряжение (φ<0) при условии, что < . Согласно (6)

(10)

Представим соотношение (2) в виде

(11)

Произведение IR равно напряжению на активном сопротивлении, q/C есть напряжение на конденсаторе U_c, выражение определяется напряжение на индуктивности U_L. С учётом этого можно написать

(12)

Таким образом, сумма напряжений на отдельных элементах контура равна в каждый момент времени напряжению, приложенному извне (1)

В соответствии с (8)

(13)

Разделив выражение (9.19) на ёмкость, получим напряжение на конденсаторе

(14)

Здесь

Умножив производную функцию (4) на L, получим напряжение на индуктивности:

(15)

Здесь

Сопоставление формул (8), (12), (14) и (15) показывает, что напряжение на ёмкости отстаёт по фазе от силы тока на π/2. Напряжение на активном сопротивлении изменяется в фазе с током.

можно показать, что резонансная частота для заряда q и напряжения на конденсаторе U_c равна:

Резонансные кривые для U_c изображены на рис. 9.6 (резонансные кривые для q имеют такой же вид). При ω→0 резонансные кривые сходятся в одной точке с ординатой U_Cm=U_m – напряжению, возникающему на конденсаторе при подключении его к источнику постоянного напряжения U_m. Максимум при резонансе получается тем выше и острее, чем меньше , т.е чем меньше активное сопротивление и больше индуктивность контура.

Рис. 2 Резонансные кривые для напряжения на конденсаторе

Резонансные кривые для силы тока приведены на рис. 2. Амплитуда силы тока имеет максимальное значение при . Следовательно, резонансная частота для силы тока совпадает с собственной частотой колебаний в контуре

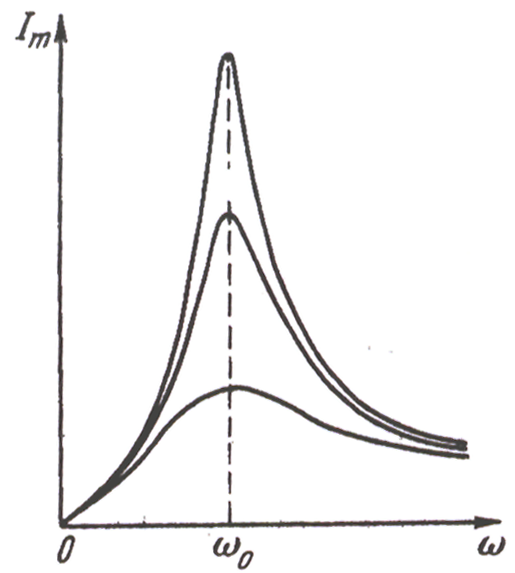
Рис. 3 Резонансные кривые для силы тока в контуре

Явление резонанса используется для выделения из сложного напряжения нужной составляющей. пусть напряжение, приложенное к контуру, равно

Настроив контур на одну из частот , и т. д. (т. е. подобрав соответствующим образом его параметры С и L), можно получить на конденсаторе напряжение, значительно превышающие напряжения других составляющих. Такой процесс осуществляется, например, при настройке радиоприёмника на нужную длину волны.