3.3.3. Общие принципы построения комбинированных моделей
Методологической основой комбинирования (самоорганизации) моделей является допущение о том, что вся информация об изменении объекта прогнозирования содержится во временных рядах характеристик этого объекта и в заданных критериях выбора модели [8, с. 24].
Общие принципы построения комбинированных моделей прогноза заключаются в следующем [11, с. 125-126]:
базовый набор моделей прогноза может формироваться или исследователем, или автоматически из множества моделей прогноза;
автоматическое формирование базового набора моделей основано на непрерывном сравнении средних квадратов ошибок прогнозов, полученных по разным моделям из множества моделей к текущему моменту времени;
при автоматическом формировании базового набора моделей в него включаются только те модели из множества моделей, средние квадраты ошибок прогноза которых не больше чем в
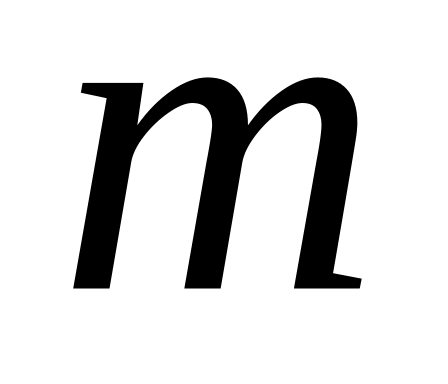раз превосходят минимальную из них
(это связано с тем, что плохие модели
могут случайно приближаться к реальному
процессу и кратковременно давать
хорошие прогнозы, что со временем
приводит к появлению больших ошибок
прогноза; поэтому такие модели
целесообразно не включать в базовый
набор);значение выбирается, как правило, в пределах от 1,2 до 1,5;
при автоматическом формировании базовый набор не является раз навсегда определённым (если с течением времени меняется соотношение между средними квадратами ошибок, то меняется соответственно и базовый набор);
число моделей в базовом наборе не целесообразно брать большим (обычно достаточно 3-4 моделей).
5-й принцип реализует один из фундаментальных методов адаптации, а именно принцип сохранения свободы выбора, или принцип неокончательных решений, который формулируется следующим образом: принимать решение в данный момент времени нужно таким образом, чтобы в последующий момент времени, где будет необходимость в очередном решении, сохранялась бы свобода выбора решений [8, с. 34-35].
Практическое применение адаптивных комбинированных моделей связано с решением ряда вопросов. Это, прежде всего, вопросы, касающиеся выбора исходного множества моделей для формирования базового набора и регулирования инерционности переключения с одной модели на другую. Решение этих вопросов считается перспективным для дальнейших исследований [11, с. 131].
РЕЗЮМЕ
Центральным моментом прогнозирования является выбор адекватной модели прогнозирования.
Проблемы выбора модели (метода) прогнозирования связаны со следующими причинами: большим количеством методов прогнозирования (больше 200); постоянным возрастанием сложности как самих решаемых задач, так и объектов прогнозирования; возрастанием динамичности прогнозного фона. Поэтому на выбор метода прогнозирования влияет множество факторов.
Проблема выбора модели прогнозирования тесно связана с проблемой точности прогноза. К основным критериям точности прогноза относятся абсолютные критерии точности (абсолютная ошибка прогноза для каждого момента времени, относительная ошибка прогноза в процентах для каждого момента времени, средняя квадратическая ошибка прогноза, среднее абсолютное отклонение прогноза, средняя процентная ошибка прогноза, средняя абсолютная ошибка в процентах).
Во многих случаях ни один из методов сам по себе не может обеспечить требуемую степень достоверности и точности прогноза, но, будучи использован в определённых сочетаниях с другими, оказывается весьма эффективным - достоинства одного метода компенсируют недостатки другого или они используются в развитии. В связи с этим в современном прогнозировании наблюдается тенденция к созданию комбинированных моделей.
Основными типами адаптивных комбинированных моделей являются адаптивные селективные и гибридные модели. Адаптивная селективная модель– это адаптивная комбинированная модель прогноза, в которой на каждом шаге прогнозирования организован автоматический выбор по заданному критерию наилучшей модели из числа моделей, входящих в базовый набор. Адаптивная гибридная модель - это адаптивная комбинированная модель прогноза, в которой прогноз формируется как взвешенная сумма прогнозов моделей базового набора.
Практическое применение адаптивных комбинированных моделей связано с решением ряда вопросов. Решение этих вопросов считается перспективным для дальнейших исследований.