2.3.4. Двухпараметрическая модель Хольта с гипотезой Тейла-Вейджа

При линейной тенденции развития процесса и при аддитивном характере сезонного эффекта используется модель прогноза Хольта с гипотезой Г. Тейла и С. Вейджа, являющаяся развитием двухпараметрической модели линейного роста Хольта.

Прогноз по данной модели на шагов вперед определяется выражением [6, с. 133]

.

Выражения для обновления коэффициентов модели имеют вид:

,

,

,

, ,

где - сглаженное значение аддитивно учитываемого сезонного фактора.

2.3.5. Трехпараметрическая модель Бокса-Дженкинса

Трехпараметрическая модель прогнозирования Дж. Бокса и Г. Дженкинса представляет собой усовершенствованную двухпараметрическую модель Хольта, которая учитывает разность ошибок прогноза. Прогноз по данной модели на шагов вперед определяется системой выражений [11, с. 36]

, (23)

, (24)

, (25)

,

где - ошибка прогнозирования.

На основе практических испытаний модели на многих экономических рядах Бокс и Дженкинс пришли к выводу, что включение в модель разности ошибок не является необходимым. Коэффициент всегда оказывался близким к нулю. Другой исследователь модели Бокса-Дженкинса П. Харрисон пришел к такому же выводу. Данный вывод исследователей модели объясняется стохастическим характером уровней временных рядов, и, в частности тем, что корреляция ошибок в таких рядах неустойчива [11, с. 37].

2.4. Модели прогнозирования стационарных временных рядов

Временные ряды многих экономических показателей имеют сложную структуру. Моделирование таких рядов на основе построения моделей тренда, сезонности и периодической составляющей не приводит к удовлетворительным результатам, так как во временном ряду остатков остаются статистические зависимости [6, с. 141; 2, с. 108]. Поэтому моделирование таких рядов производится путем предварительного приведения их к стационарному виду за счет выполнения операций выделения тренда и устранения сезонной компоненты, поскольку ряд остатков , как правило, является стационарным [6, с. 141].

К наиболее распространенным моделям стационарных временных рядов относятся: 1) модели авторегрессии; 2) модели скользящего среднего; 3) модели авторегрессии-скользящего среднего.

2.4.1. Модели авторегрессии

Моделью авторегрессии порядка называется модель стационарного процесса, выражающая значение уровня временного ряда в виде линейной комбинации конечного числа предшествующих ему значений и аддитивной случайной составляющей [2, с. 108]. В англоязычной статистической литературе эти модели называются AutoRegressive processes of order и кратко обозначаются AR( )-models. Модель авторегрессии порядка имеет вид [6, с 141]

,

где - белый шум, то есть последовательность случайных величин, удовлетворяющих следующим условиям:

1. ;

2. 

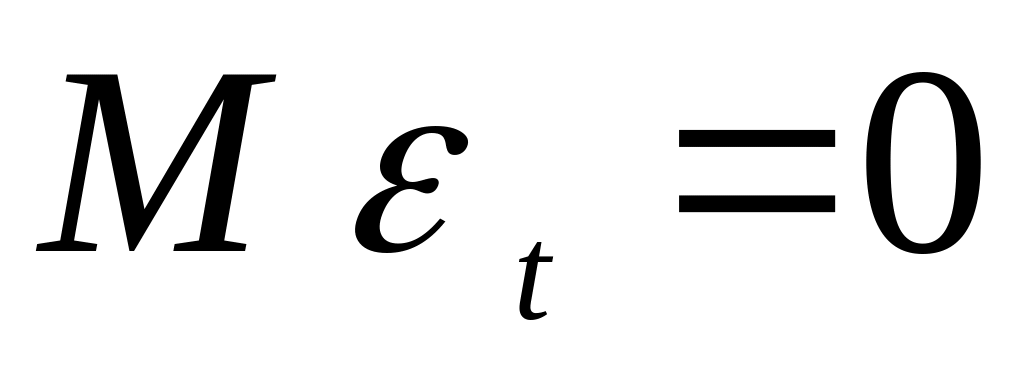Наиболее часто на практике используются авторегрессионные модели первого и второго порядков.

Модель авторегрессии первого порядка AR(1) определяется выражением вида [6, с. 142]

,

(условие стационарности AR(1)).

В модели авторегрессии первого порядка параметр имеет смысл коэффициента автокорреляции первого порядка, то есть [2, с. 109].

Модель авторегрессии первого порядка называется также марковским процессом. Марковскими процессами называются процессы, в которых состояние объекта в каждый следующий момент времени определяется только его состоянием в настоящий момент времени и не зависит от того, каким путем объект достиг этого состояния [2, с. 108-109]. В терминах корреляционного анализа для временных рядов марковский процесс представляет собой процесс, в котором существует статистически значимая корреляционная связь исходного ряда с рядом, сдвинутым на один временной интервал, и в котором эта связь отсутствует с рядами, сдвинутыми на два, три и т. д. временных интервала [2, с. 109].

В общем случае прогнозирование с использованием модели авторегрессии включает следующие этапы [2, с. 111]:

1. выделение неслучайной составляющей 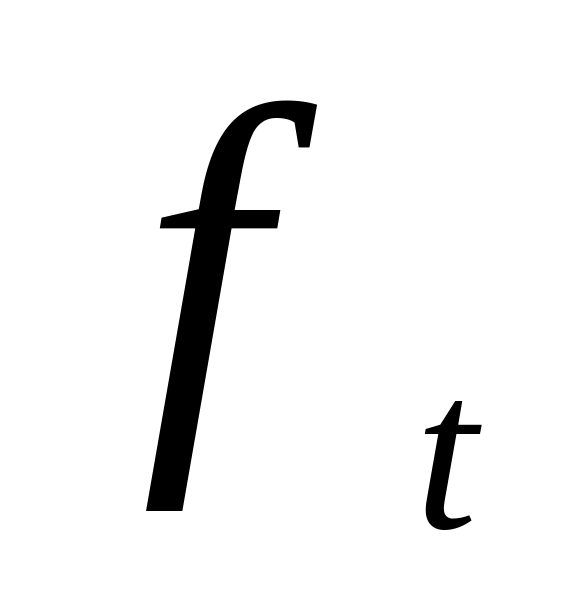и расчет остатков ;

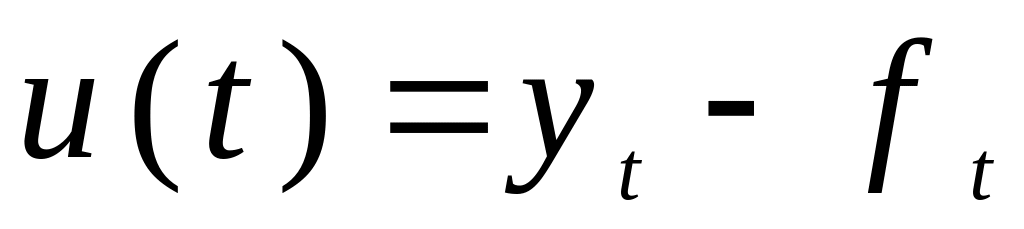2. проверка полученного ряда на стационарность;

3. определение порядка модели ;

4. идентификация модели;

5. экономическое истолкование модели и построение прогноза.

Идентификация модели – это статистическое оценивание ее параметров по имеющейся реализации временного ряда [16, с. 250]. Идентификация модели авторегрессии первого порядка выполняется в следующей последовательности [2, с. 111-112; 16, с. 251]:

1. вычисление выборочной дисперсии остатков по формул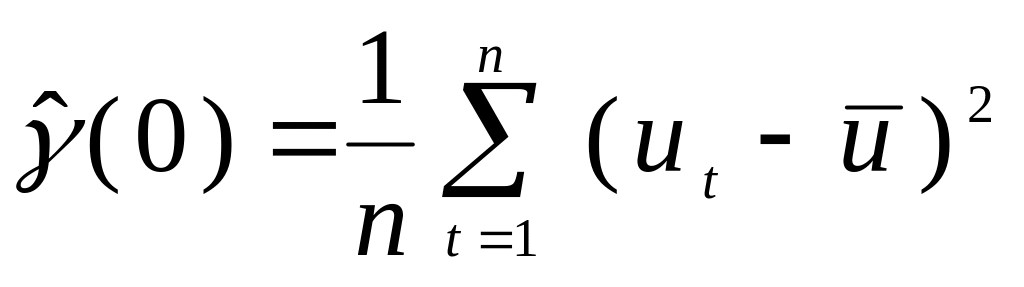е , где 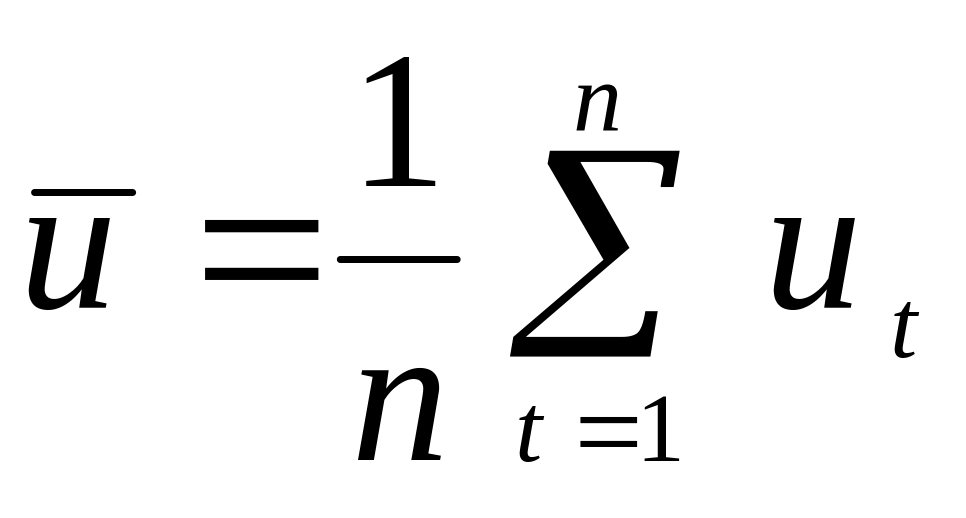- выборочное среднее значение остатков;

2. расчет выборочного коэффициента автокорреляции по формуле

;

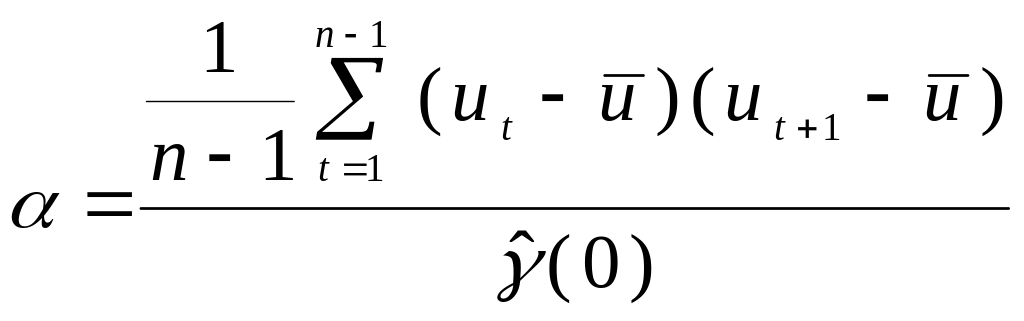3. оценка дисперсии белого шума по формуле .

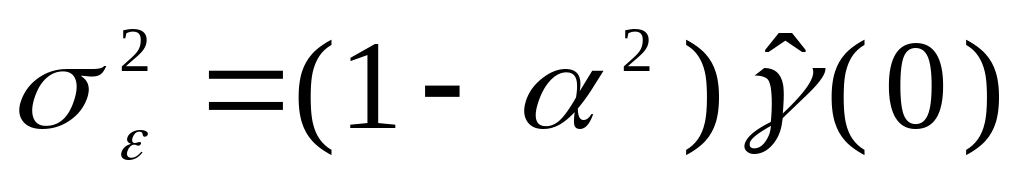Модель авторегрессии второго порядка AR(2), называемая также процессом Юла, определяется выражением вида [2, с. 113; 6, с. 146]

.

Необходимые и достаточные условия стационарности данной модели имеют вид [6, с. 148; 16, с. 254]:

Идентификация модели авторегрессии второго порядка выполняется в следующей последовательности [2, с. 116; 16, с. 257-258]:

1. вычисление выборочной дисперсии остатков по формуле

;

2. оценка коэффициентов автокорреляции первого и второго порядков по формуле

, ;

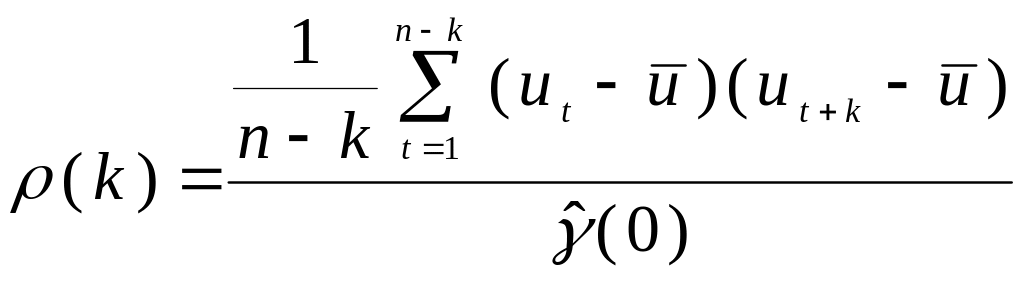допустимые значения этих коэффициентов, обеспечивающие стационарность модели AR(2) должны принадлежать области вида

3. вычисление параметров авторегрессии по формулам

, ;

4. оценка дисперсии белого шума по формуле

.

Идентификация моделей авторегрессии связана с проблемой, заключающейся в том, что оценка значений коэффициентов автокорреляции при реальных соотношениях объема выборки имеющихся уровней динамического ряда и горизонта планирования дает, как правило, неудовлетворительный результат [16, с. 251]. Поэтому в [19, с. 435] описан упрощенный вариант прогнозной модели авторегрессии вида

, ,

в котором оценки параметров авторегрессии вычисляются методом наименьших квадратов для множественной линейной регрессии зависимой переменной , представленной исходным временным рядом, на объясняющие переменные , , … , которые характеризуются тем же временным рядом, но сдвинутым соответственно на 1, 2, … периодов вперед.