3.3. Комбинированные модели краткосрочного прогноза

Во многих случаях ни один из методов сам по себе не может обеспечить требуемую степень достоверности и точности прогноза, но, будучи использован в определённых сочетаниях с другими, оказывается весьма эффективным - достоинства одного метода компенсируют недостатки другого или они используются в развитии [10, с. 35].

Объективная необходимость в комбинировании различных методов, как правило, возникает при разработке прогнозов развития процессов, характеризующихся наличием сложных взаимосвязей [10, с. 35]. В таких случаях реальный процесс время от времени претерпевает коренные изменения, заключающиеся в изменении уровня и динамических свойств ряда. Причём на одних участках сохраняется приблизительно постоянный уровень, на других ряд растёт с определённой скоростью или характеризуется появлением ускорения. Поэтому всякая попытка подобрать какую-либо одну прогнозную модель для всего ряда приводит к существенным ошибкам прогноза [11, с. 121]. В связи с этим в современном прогнозировании наблюдается явная тенденция к созданию комбинированных моделей [18, с. 239].

Адаптивная комбинированная модель прогноза – это модель прогноза, состоящая из нескольких простых адаптивных моделей прогноза, называемых базовым набором моделей [11, с. 121].

Основными типами адаптивных комбинированных моделей являются адаптивные селективные и гибридные модели.

3.3.1. Адаптивные селективные модели

Адаптивная селективная модель прогноза – это адаптивная комбинированная модель прогноза, в которой на каждом шаге прогнозирования организован автоматический выбор по заданному критерию наилучшей модели из числа моделей, входящих в базовый набор. В такой модели адаптация происходят на двух уровнях: по структуре (или типу) модели и по параметрам модели [11, с. 121].

Общие принципы построения адаптивных селективных моделей заключаются в следующем [11, с. 122-123]:

1. вычисление прогнозных значений динамического ряда осуществляется по каждой модели в отдельности, но в качестве прогноза выбирается прогноз модели, наилучшим образом отражающей реальный процесс на данном временном интервале;

2. наилучшая модель выбирается в соответствии с заданным критерием селекции;

3. наилучшей считается модель с минимальной абсолютной ошибкой прогноза;

4. в общем случае нельзя исходить только из последней ошибки прогноза (необходимо учитывать некоторую их совокупность).

Имеется много вариантов построения критерия селекции. Примерами таких критериев являются [11, с. 123]:

1. критерий К, когда переключение на данную модель осуществляется тогда, когда К её последних прогнозов являются наилучшими в сравнении с прогнозами других моделей базового набора;

2. критерий В, когда переключение на данную модель осуществляется тогда, когда её экспоненциально сглаженный квадрат ошибки прогноза В минимален по сравнению с аналогичным показателем для остальных моделей базового набора.

3.3.2. Адаптивные гибридные модели

Адаптивная селективная модель рассчитана на выбор одной модели из базового набора моделей. Однако, такой выбор можно однозначно осуществить только в том случае, когда модели, входящие в базовый набор, существенно различны. В случаях, когда в базовый набор входят модели, дающие сравнительно близкие результаты, и селекция затруднена, используются адаптивные гибридные модели [11, с. 124].

Адаптивная гибридная модель прогноза – это адаптивная комбинированная модель прогноза, в которой прогноз формируется как взвешенная сумма прогнозов моделей базового набора. При этом веса моделей имеют адаптивный характер [11, с. 121].

Получаемый в данном случае прогноз будет ближе к результату, получаемому то по одной, то по другой модели, являясь некоторой адаптивной равнодействующей. В отличие от адаптивной селективной модели гибридная модель как бы осуществляет переключение с одной модели на другую более плавно с множеством промежуточных состояний [11, с. 125].

Прогнозное значение гибридной модели на один шаг вперёд может быть вычислено, например, как взвешенное среднее прогнозов отдельных моделей из базового набора по формуле [13, с. 197]

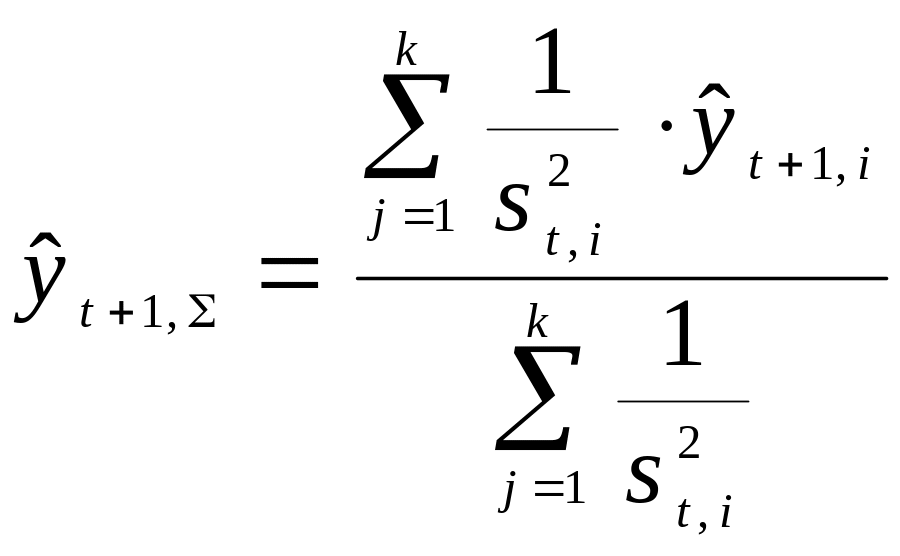, (33)

где - прогнозное значение -ой модели из базового набора на момент времени ( );

- дисперсия абсолютной ошибки прогноза -ой модели из базового набора к моменту времени .

При построении гибридных моделей необходимо учитывать следующие два обстоятельства [13, с. 198-199].

1. Прогнозные значения, вычисленные с использованием разных моделей из базового набора по формуле (33), должны быть статистически независимыми. Считается, что если в моделях для выделения тренда используются существенно разные функции (например, одна полиномиальная, а вторая экспоненциальная), то прогнозные значения таких моделей независимы. Если в моделях для выделения тренда используются родственные функции, то вопрос о независимости прогнозных значений остаётся открытым.

2. При комбинировании прогнозов неявно предполагается, что прогнозные значения каждой модели не имеют регулярного сдвига ни в сторону увеличения, ни в сторону уменьшения. Однако прогнозные значения реальных социально-экономических рядов имеют регулярные сдвиги в ту или другую сторону. Поэтому комбинирование прогнозов целесообразно, если имеются сдвиги прогнозных значений в разные стороны. В противном случае можно получить “ещё дальше сдвинутые” прогнозы.