Самореализующиеся прогнозы

Самореализующийся прогноз – социально-экономическое явление, состоящее в наличии социального механизма, приводящего к [не] реализации любого прогноза [высказанного в определённых условиях].

Пример – показ моды, как её прогноз.

В основе механизма лежит столкновение интересов, которое можно описать в терминах т.н. «теории игр» матрицей выигрыша.

Особенно силён этот механизм в биржевой торговле.

Рис. показывает модель поведения брокера фьючерсных контрактов. Задача брокера – заключить сейчас контракт по цене, которая сложится в будущем, т.е. угадать фьючерсный курс (цену). Потери брокера прямопропорциональны размеру неугадывания. Рассмотрим выигрыш (=проигрыш) брокера для диапазона цен 50-100.

Пусть текущее ожидание будущей цены – $70. Брокер, заключив контракт по этой цене, имеет минимальный проигрыш – 0. Вообще говоря, ему абсолютно все равно, по какой цене правильно заключить контракт (50 или 90, или любой прочей). Точно такое же положение у всех брокеров. Если появится прогноз повышения курсов, у брокера появляется стремление следовать этому прогнозу. Таким образом, прогноз осуществляется. Аналогично для прогноза спада.

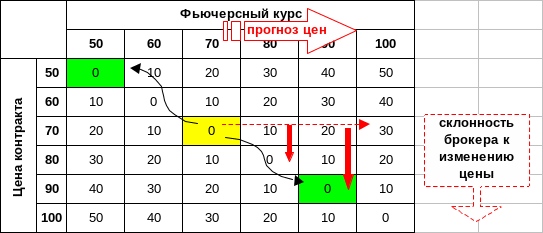
Рис. 30. Механизм самореализации прогнозов.

Возможность возникновения данного эффекта необходимо учитывать при организации прогнозирования.

Раздел 1.Основные модели краткосрочного прогноза

2.1. Упрощенные модели краткосрочного прогноза

В общем случае модель краткосрочного прогноза имеет вид [21, с. 154]

, (1)

где - прогнозное (оценочное) значение уровня динамического ряда показателя на момент времени , полученное в момент времени ;

- количество периодов времени, на которое производится прогноз;

- фактические (наблюдавшиеся) значения уровня динамического ряда показателя в моменты времени .

Наивное прогнозирование - прогнозирование, основанное на предположении, что предыдущее значение лучше всего предсказывает будущее. Группа простейших (наивных, упрощенных) моделей краткосрочного прогноза объединяет модели, которые используются при недостатке информации о динамике значений прогнозируемых показателей. Прогноз, полученный с использованием этих моделей, не отличается высокой точностью, но дает некоторое приближенное представление о возможном значении исследуемого параметра в будущем [3, с. 51].

2.1.1. Наивная модель на основе предыдущего значения показателя

Наиболее простой (“наивный”) способ прогнозирования основан на предположении, что уровень ряда остается неизменным [21, с. 156]. Простейшая модель прогноза на один интервал вперед в этом случае имеет вид [16, с. 402; 18, с. 55; 21, с. 156]

, (2)

где - прогнозное (оценочное) значение на момент времени , полученное в момент времени ;

- фактическое (наблюдавшееся) значение в момент времени .

Идея наивной модели (2) заключается в предположении, что прогнозное значение приближённо равно предыдущему значению [18, с. 55].

Использование простейшей модели (2) в прогнозировании дает хорошие результаты, если наблюдения производятся через короткие периоды времени и характер их изменения не содержит заметных скачков. В некоторых случаях данная наивная модель может давать более точные прогнозные значения, чем сложные прогнозирующие модели [19, с. 402].