Понятие о квантовой теории Дебая для теплоемкости твердых тел

В теории Дебая (1912 г.), далее развитой Борном, кристалл рассматривается как сплошное (непрерывное) упругое тело (атомы которого очень связаны между собой), участвующее в колебаниях со всевозможными частотами. Тепловые колебания отождествляются с упругими стоячими волнами в теле. Простейшей аналогией таких колебаний являются колебания натянутой струны. Число возможных колебательных состояний принимается равным числу степеней свободы , причем берутся наиболее медленные, т.е. основные колебания. Частоты этих, так называемых нормальных колебаний, весьма различны, начиная от низких, в сотни герц, и кончая инфракрасными, порядка герц. Суперпозиция этих колебаний с различными случайными амплитудами и фазами дает тепловое движение твердого тела. Величина энергии этого движения

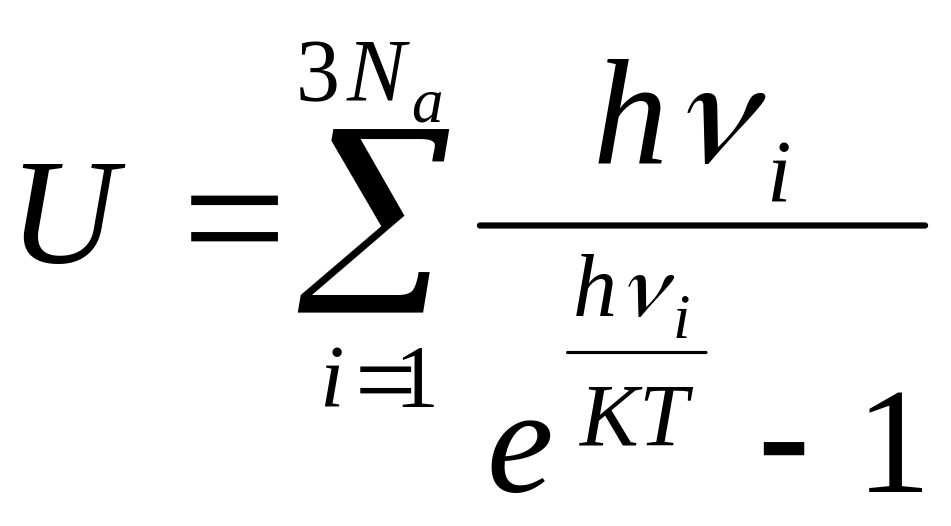(19)

Вычисление нормальных частот является весьма трудной задачей. Результаты вычисления хорошо совпадают с опытом.

Из теории Дебая следует, что при очень низких температурах теплоемкость одноатомного твердого тела пропорциональна третьей степени абсолютной температуры:

= а . (20)

Это закон кубов Дебая, который хорошо объясняет ход теплоемкости вблизи нуля. Внутренняя энергия твердого тела вблизи абсолютного нуля пропорциональна четвертой степени абсолютной температуры (U~ ). При высоких температурах теория Дебая привела к результатам, совпадающим с классическими результатами (закон Дюлонга и Пти).

Весьма важную роль в теории Дебая играет понятие характеристической температуры Дебая , начиная с которой теплоемкость быстро убывает с понижением температуры. Это та температура, при которой энергия тепловых движений k становится равной максимальной энергии осцилляторов: , отсюда:

. (21)

При температурах, значительно меньших , теплоемкость убывает пропорционально кубу температуры, что соответствует опытным данным. Температура Дебая может считаться границей между высокими и низкими температурами. При температуре выше теплоемкость следует классическому закону, ниже – для объяснения зависимости (Т) необходимо использовать квантовые представления. С точки зрения квантовой теории теплоемкости тот факт, что некоторые вещества (алмаз, бор и др.) не подчиняются закону Дюлонга и Пти даже при комнатных температурах, объясняется именно тем, что у этих веществ температура Дебая настолько высока, что комнатная температура должна считаться низкой температурой. Так, если для серебра =210⁰С, для алюминия ≈ 400⁰С, для свинца ≈ 90⁰С, то для алмаза равна 2000⁰С. Вместе с тем, если температуру тела нормировать на температуру Дебая, то ход температурных зависимостей теплоемкости различных веществ, отнесенный к числу атомов в молекуле данного вещества n, весьма близок. (Рис.2)

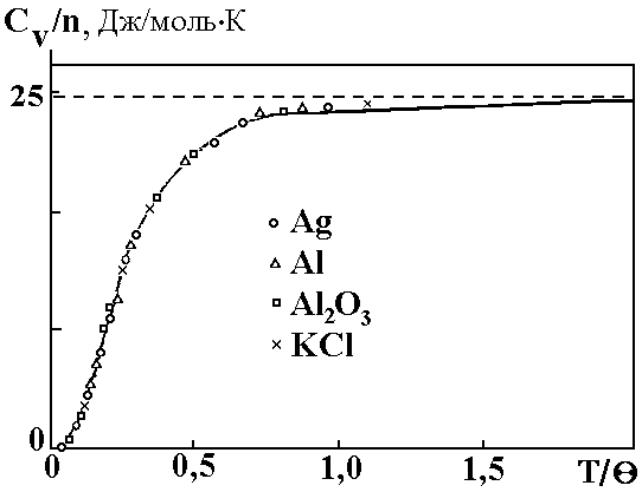
Рис.2. Температурные зависимости теплоемкости различных веществ

В табл.1 приведены численные значения температуры Дебая для некоторых простых и сложных кристаллических соединений.

Таблица 1

Значения температуры Дебая для некоторых типичных твердых тел

Кристалл	, К, определенная по упругим постоянным	, К, определенная по теплоемкости при низких температурах
Алюминий Свинец NaCl LiF	438 135 289 610	423 102 321 732

Измерения теплоемкости и ее температурного хода играют большую роль в исследованиях твердых тел. Это связано с тем, что теплоемкость непосредственно определяется колебаниями атомов в кристаллической решетке. Характер этих колебаний должен зависеть от структуры решетки, ее симметрии и т.д. Поэтому различные аномалии теплоемкости, наблюдаемые в веществе, могут дать информацию о характерных для него внутренних превращениях. Так, фазовый переход второго рода в кристалле, в результате которого происходит изменение структуры его решетки, мы можем обнаружить по скачкообразному изменению его теплоемкости.