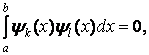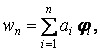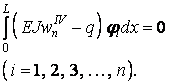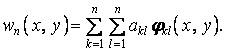- •1.1 Гіпотези й принципи теорії пружності
- •1.2 Напружений стан в точці тіла. Тензор напруг
- •1.2.1 Зовнішні сили й напруги
- •1.2.2 Диференціальні рівняння рівноваги
- •1.2.3 Визначення напруг на похилих площадках. Умови на поверхні
- •1.2.4 Головні напруги. Інваріанти напруженого стану
- •1.2.5 Тензор напруг. Найбільші дотичні напруження
- •1.3 Деформований стан у точці тіла. Тензор деформацій
- •1.3.1 Переміщення й деформації. Взаємозв'язок між ними
- •1.3.2 Об'ємна деформація
- •1.3.3 Рівняння нерозривності деформацій
- •1.3.4 Тензор деформацій. Головні деформації
- •1.4 Взаємозв'язок між тензорами напруг і деформацій. Узагальнений закон Гука
- •1.5 Робота пружних сил. Потенційна енергія деформацій
- •2.1 Повна система рівнянь теорії пружності
- •2.2 Розв’язання задач теорії пружності в переміщеннях
- •2.3 Рішення задачі теорії пружності в напруженнях при постійних об'ємних силах
- •2.4 Типи граничних умов на поверхні тіла
- •2.5 Теорема одиничності. Методи рішення задачі теорії пружності
- •3.1 Плоска деформація і плоский напружений стан
- •3.2 Методи рішення плоскої задачі для прямокутних однозв'язних областей
- •3.3 Згинання консолі силою, прикладеною на кінці
- •3.4 Балка на двох опорах під дією рівномірно розподіленого навантаження
- •3.5 Трикутна підпірна стінка
- •3.6 Розрахунок балки-стінки
- •3.7 Обґрунтування принципу Сен-Венана
- •Розділ 4. ПлосКа задача теорії пружності у полярних координатах
- •4.1 Основні рівняння
- •4.2 Простий радіальний напружений стан
- •4.3 Клин, навантажений у вершині зосередженою силою
- •4.4 Стискання клина
- •4.5 Згинання клина
- •4.6 Дія зосередженої сили, прикладеної до границі напівплощини
- •4.7 Функція напружень для плоскої задачі в полярних координатах
- •4.8 Осесимметричні задачі. Рішення в переміщеннях
- •4.9 Розрахунок труби з товстими стінками (задача Ламе)
- •4.10 Рішення осесимметричної задачі за допомогою функції напружень
- •4.11 Чистий вигин криволінійного бруса. Задача Головіна
- •4.12 Поняття про розрахунок циліндричних котків
- •6.13 Поняття про дію зосередженої сили на пружний півпростір
- •5.1 Основні поняття й гіпотези
- •5.2 Переміщення і деформації в пластинці
- •5.3 Напруження в пластинці
- •5.4 Зусилля в пластинці
- •5.5 Вираження напружень через зусилля
- •5.6 Диференційне рівняння зігнутої серединної поверхні пластинки
- •5.7 Умови на контурі пластинки
- •5.8 Прямокутна пластинка. Рішення Нав’є
- •5.9 Прямокутна пластинка. Розв’язок Леві
- •5.10 Поняття про розрахунок прямокутної пластинки й нескінченної смуги на пружній основі
- •5.11 Основні рівняння вигину круглої пластинки
- •5.12 Найпростіші осесиметричні задачі вигину круглої пластинки
- •5.13 Поняття про розрахунок гнучких пластинок
- •6.1 Сутність варіаційних методів розв’язання
- •6.2 Метод Рітца-Тимошенко
- •6.1 Сутність варіаційних методів розв’язання
- •6.2 Метод Рітца-Тимошенко
- •6.3 Метод Бубнова-Гальоркіна
- •6.4 Метод Власова
- •6.5 Потенційна енергія при вигині пластинки
- •6.6 Приклад розв’язання задачі методом Рітца-Тимошенко
- •6.7 Приклад розв’язання задачі методом Бубнова-Гальоркіна
6.3 Метод Бубнова-Гальоркіна
Метод Бубнова—Гальоркіна заснований на властивості ортогональності функцій. У курсі математичного аналізу дається наступне визначення ортогональних функцій: якщо є сімейство безперервних функцій
![]() (а)
(а)
і
інтеграл добутку будь-яких двох різних
функцій цього сімейства в проміжку
![]() дорівнює нулю:
дорівнює нулю:
|
(6.6) |
ці функції (а) утворять у цьому проміжку ортогональну систему. Наприклад, сімейство тригонометричних функцій
|
(б) |
є
ортогональною системою
в проміжку
![]()
Дійсно,
|
(в) |
причому, ці інтеграли вичерпують усілякі варіанти комбінування двох різних функцій сімейства (б).
На
підставі леми з курсу математичного
аналізу слідує: якщо одна з функцій
тотожно дорівнює нулю, наприклад
![]() ,
то вона ортогональна до всіх без винятку
функцій, тому що в цьому випадку
виконується умова (6.6). Як приклад можна
привести функцію
,
то вона ортогональна до всіх без винятку
функцій, тому що в цьому випадку
виконується умова (6.6). Як приклад можна
привести функцію
|
(г) |
яка представляє собою ліву частину диференціального рівняння вигнутої осі балки. Ця функція тотожно рівна нулю при будь-яких значеннях x, і, відповідно,
![]()
Тут
інтеграл береться по всій довжині балки
L,
і тому функція (г) ортогональна в проміжку
![]() до будь-якої функції.
до будь-якої функції.
Якщо функцію прогинів замінити її наближеним виразом у формі ряду
|
(д) |
то
функція (г) уже не буде тотожно дорівнює
нулю, а виходить, і не буде ортогональна
в зазначеному проміжку до будь-якої
функції. Можна, однак, зажадати, щоб вона
була ортогональна хоча б до обмеженого
класу функцій, наприклад функцій
![]() ,
що становлять ряд (д), тобто щоб
,
що становлять ряд (д), тобто щоб
|
(е) |
У результаті одержимо n лінійних рівнянь для визначення n постійних коефіцієнтів , що входять у ряд (д).
На використанні системи рівнянь (е) для визначення значень параметрів і заснований метод Бубнова-Гальоркіна. Всі міркування, наведені для функції одного аргументу, можна застосувати й до функцій двох аргументів і більше. Для розв’язання задач про вигин пластинок рівняння Бубнова-Гальоркіна (е) можна представити у вигляді
|
(6.7) |
де замість лінійного проміжку розглядається плоска область s, обмежена контуром пластинки, а функція виражається наступним подвійним рядом по області s:
|
(ж) |
Таким чином, наближена функція в рівняннях (6.7), що представляє собою ліву частину диференціального рівняння вигнутої серединної поверхні пластинки (5.16), ортогональна в області s до всіх функцій ряду (ж), що входить у цю наближену функцію.
Методу
Бубнова-Гальоркіна можна дати й інше,
тлумачення. Функція
![]() являє собою проекцію на вісь z
всіх зовнішніх і внутрішніх сил, що
діють на нескінченно малий елемент
пластинки. Функція прогинів
є переміщення в напрямку тої ж осі.
Виходить, функції
теж є переміщеннями в напрямку осі z
і їх можна вважати можливими переміщеннями.
Отже, рівняння Бубнова-Гальоркіна (6.7)
приблизно виражають рівність нулю
роботи всіх зовнішніх і внутрішніх сил
у пластинці на можливих переміщеннях
.
являє собою проекцію на вісь z
всіх зовнішніх і внутрішніх сил, що
діють на нескінченно малий елемент
пластинки. Функція прогинів
є переміщення в напрямку тої ж осі.
Виходить, функції
теж є переміщеннями в напрямку осі z
і їх можна вважати можливими переміщеннями.
Отже, рівняння Бубнова-Гальоркіна (6.7)
приблизно виражають рівність нулю
роботи всіх зовнішніх і внутрішніх сил
у пластинці на можливих переміщеннях
.
Таким чином, метод Бубнова-Гальоркіна, як і метод Рітца-Тимошенко, виходить із принципу можливих переміщень, обидва методи рівноправні. В обох випадках апроксимуючу функцію необхідно вибирати так, щоб вона задовольняла геометричним граничним умовам. Виконання статичних умов не обов'язково.