5.2 Переміщення і деформації в пластинці

Вивчення згинання пластинки почнемо з визначення переміщень і деформацій. Досліджуємо пластинку, що несе поперечне навантаження, тобто навантаження, нормальну до серединної площини пластинки. Під дією цього навантаження пластинка одержить переміщення. Для їх визначення звернемося до прийнятих гіпотез.

Слідуя першій гіпотезі й підставляючи умову (5.2) у третю з формул (2.3), одержуємо

,

звідки виходить, що прогини пластинки не залежать від координати , тобто

.

Це означає, що всі точки пластинки, що лежать на одній вертикалі, одержують однакові переміщення . Отже, досить визначити прогини серединної площини пластинки, щоб знати вертикальні переміщення всіх її точок.

Розглядаючи умови для зсувів (5.1), з формул (2.3) одержуємо

;

;

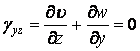звідси знаходимо похідні складових переміщення й :

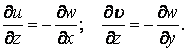
Інтегруючи ці рівняння по , одержуємо

(а)

Для обчислення функцій і , що з'явилися при інтегруванні рівнянь у частних похідних, скористаємося гіпотезою про недеформованість серединної площини. Підставляючи умови (5.3) у формули (а) при , одержуємо:

Тоді формули (а) приймають вид

(5.4)

Таким чином, складові переміщення точок пластинки в напрямках осей і виражені через функцію прогинів серединної площини пластинки.

Складові деформації пластинки, відмінні від нуля, знаходимо за допомогою формул (2.3), підставляючи в них значення складових переміщення (5.4):

(5.5)

Тут складові деформації, так само як і складові переміщення в співвідношеннях (5.4), виражені через одну функцію прогинів серединної площини пластинки.

5.3 Напруження в пластинці

Для обчислення нормальних напружень і скористаємося двома першими формулами закону Гука (2.5) і на підставі третьої гіпотези відкинемо напруження . Тоді одержимо:

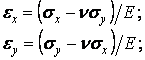
звідси з урахуванням залежностей (5.5) знаходимо

(а)

Четверта формула закону Гука після підстановки кутової деформації з формул (5.5) приймає такий вид:

(б)

Дотичні напруження у двох інших площинах, відповідно до рівностей (5.1), звертаються в нуль:

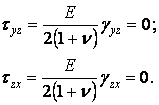
Однак такий результат отриманий тільки внаслідок прийнятих раніше гіпотез. У дійсності ці дотичні напруження не дорівнюють нулю, оскільки це суперечить умовам рівноваги. Дійсно, розглянемо диференціальні рівняння рівноваги (2.1). Зневажаючи об'ємними силами, з першого рівняння знаходимо

.

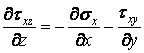Підставимо сюди напруження з формул (а) і (б):

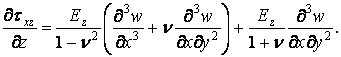
Після спрощення одержуємо

або

Інтегруючи по , знаходимо

(в)

Для визначення довільної функції маємо наступні граничні умови: на верхній і нижній поверхнях пластинки немає дотичних навантажень, тобто при . Підставляючи ці умови у формулу (в), одержуємо

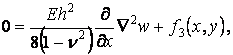
звідки шукана функція

.

Якщо ввести її у формулу (в), одержуємо

.

(г)

Вирішуючи таким же шляхом друге рівняння рівноваги (2.1), знаходимо

.

(д)

Отже, відповідно до формул (а), (б), (г) і (д), у перерізах пластинки, перпендикулярних її серединнії площини, виникають наступні напруження:

(5.6)

На рис. 5.2 показані епюри цих напружень по товщині пластинки.

Рис. 5.2. Епюри напружень по товщині пластинки

Напруження й розподіляються за лінійним законом, звертаючись у нуль в точках серединної площини; напруження і розподіляються по параболі, досягаючи в точках серединної площини максимального значення. Так само розподіляються дотичні напруження і при поперечному згинанні балок прямокутного перерізу.

У формулах (5.6) всі напруження виражені через одну функцію двох змінних , отже, функція прогинів грає тут такуж роль, що й функція напружень у плоскої задачі.
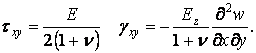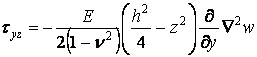