4.10 Рішення осесимметричної задачі за допомогою функції напружень
Знайдемо
функцію напружень осесимметричної
задачі. Бігармонічне рівняння
осесимметричної задачі (4.27) являє собою
диференціальне рівняння зі змінними
коефіцієнтами. Щоб одержати рівняння
з постійними коефіцієнтами, переходимо
до нової змінної
за допомогою підстановки (4.32). Зв'язок
між похідними функції
по старій і новій змінним установлюємо
аналогічно тому, як це зроблено в 4.8.
Підставляючи вирази похідних у рівняння (4.27), одержимо лінійне однорідне диференціальне рівняння з постійними коефіцієнтами
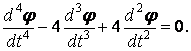
Його рішення має вигляд
.
Переходячи до старої змінної , одержуємо загальне рішення рівняння (4.27):
|
(4.39) |
.По формулах (4.28) знаходимо напруження:
|
(4.40) |
Отримані
рівняння являють собою загальне рішення
осесимметричної задачі. Залишається
лише визначити із граничних умов значення
постійних
і
.
4.11 Чистий вигин криволінійного бруса. Задача Головіна
При чистому згинанні криволінійного бруса, вісь якого обкреслена по дузі окружності (рис. 4.13), розподіл напружень у всіх радіальних перерізах однакове. Отже, напруження в такому брусі можна визначати по формулах (4.40).
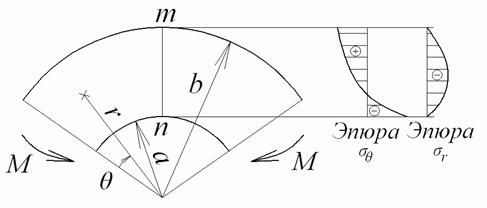
Рис. 4.13. Чисте згинання криволінійного бруса
Для визначення вхідних у ці формули постійних маємо наступні умови на криволінійних поверхнях:
при
|
(а) |
при
|
(б) |
На торцях рівнодіюча зусиль повинна бути дорівнює нулю, тобто
|
(в) |
,і тому ці зусилля повинні приводитися до пари з моментом :
|
(г) |
.
Умови
(а) і (б) для дотичних напружень
виконуються тотожно, а відносно нормальних
напружень після підстановки першої
формули (4.40) приводяться до наступних
рівнянь:
|
(д) |
|
(е) |
;
.Умова (в) приймає наступний розгорнутий вид:
,
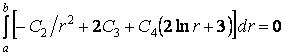звідки після інтегрування
|
(ж) |
.Аналогічно з умови (г) у вигляді
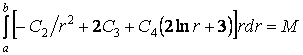
після інтегрування одержуємо
.
Неважко бачити, що при виконанні умов (д) і (е) умова задовольняється тотожно. Вирішуючи спільно рівняння (д), (е) і (з), одержуємо:
;
.
Тут введене позначення:
.
Підставляючи отримані постійні у формули (4.40), знаходимо
|
(4.41) |
Епюри напружень і побудовані на рис. 4.13.
Точне рішення задачі про чисте згинання, а також задача про поперечне згинання криволінійного бруса вперше отримане в 1881 р. X. С. Головіним.
Порівнюючи формули (4.41) і (3.23), зауважуємо, що на відміну від прямого бруса при чистому згинанні криволінійного існує тиск волокон один на одного. В опорі матеріалів рішення задачі чистого згинання криволінійного бруса засновано на гіпотезі плоских перерезів і допущенні про відсутність тиску поздовжніх волокон один на одного. При цьому виходять наступні результати:
|
(4.42) |
де
— площа
поперечного переріза;
— відстань від центра ваги перерізу до
нейтральної осі;
— середній радіус кривизни бруса.
У табл.
4.1 наведені результати обчислення
напружень по формулах (4.41) і (4.42) для
бруса великої кривизни, коли висота
перерізу
або радіус
.
Найбільше значення напруження
,
отримане методом теорії пружності,
прийнято за одиницю.
Таблиця 4.1
Порівняння результатів теорії пружності та опору матеріалів
Формули |
|
|
|
при |
при
|
||
Теорії пружності (4.41) |
–1,000 |
0,492 |
–0,192 |
Опору матеріалів (4.42) |
–1,005 |
0,480 |
0 |
Розбіжність, % |
0,5 |
2,5 |
-- |
Як видно
з таблиці, навіть при дуже великій
кривизні бруса рішення опору матеріалів
відносно нормального напруження
відрізняється всього на 2,5% від точного
рішення. Максимальні нормальні напруження
становлять 19,2% від
,
однак вони виникають у точках, де
напруження
близькі до нуля, і, отже, не мають значення
при оцінці міцності. Тому при розрахунку
криволінійних брусів рішення опору
матеріалів цілком прийнятно.
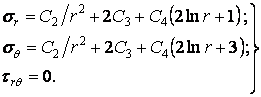
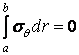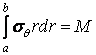