Розв’язування

а) Для того, щоб дана функція була щільністю ймовірності неперервної випадкової величини, вона повинна бути невід’ємною, тобто , і . Таким чином,

, звідки .

б) За формулою (1.22) знайдемо .

Якщо , то .

Якщо , то .

Таким чином,

.

в) За формулою (1.21) маємо

.

Ймовірність можна знайти за формулою (1.19):

г) За формулою (1.24) маємо

.

Дисперсію обчислимо за формулою (1.26). Для цього спочатку знайдемо

тоді

6. Мода, медіана, квантилі, моменти випадкових величин. Асиметрія та ексцес (надвишок)

Модою (fashion) випадкової величини називається її найімовірніше значення (для якого ймовірність або щільність ймовірності набуває максимального значення). Якщо ймовірність або щільність ймовірності набуває максимального значення в декількох точках, то такий розподіл називають полімодальним (рис. 1.8)

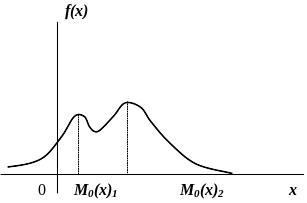
Рисунок 1.8

Медіаною неперервної випадкової величини називається таке її значення, для якого

. (1.27)

З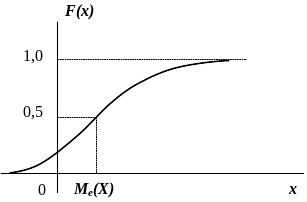 геометричної точки зору, пряма ділить площу фігури під кривою розподілу на дві рівні частини. Зрозуміло, що (рис. 1.9).

Рисунок 1.9

Квантилем рівня ( quantile of level q) (або -квантилем) називають таке значення випадкової величини при якому

. (1.28)

Деякі квантилі мають особливу назву. Наприклад, медіана – квантилі рівня 0,5, а квантилі та називають відповідно верхнім та нижнім квантилем. З поняттям квантиля тісно пов’язане поняття відсоткової точки. 100% точкою називають квантиль , тобто таке значення випадкової величини , при якому .

Приклад 1.13 Знайти квантиль та 30%-ву точку випадкової величини із щільністю ймовірності при .

Розв’язування

За формулою (1.22) функція розподілу

.

Квантиль знайдемо за формулою (1.28), тобто або . Звідки . Знайдемо 30%-ву точку випадкової величини або квантиль з рівняння , звідки .

Початковим моментом -го порядку випадкової величини називають математичне сподівання -го степеня цієї величини:

. (1.29)

Центральним моментом -го порядку (central moment of order k) випадкової величини називають математичне сподівання -го степеня відхилення випадкової величини від її математичного сподівання:

. (1.30)

Якщо позначити , то формули для обчислення моментів дискретних та неперервних випадкових величин можна подати у вигляді таблиці (табл. 1.1).

Таблиця 1.1

Момент	Випадкова величини
	Дискретна	Неперервна
Початковий	(1.31)	(1.32)
Центральний	(1.33)	(1.34)

Легко помітити, що перший початковий момент ( ) випадкової величини – математичне сподівання , а другий центральний момент – дисперсія випадкової величини .

Третій центральний момент характеризує асиметрію розподілу. Він має розмірність кубу випадкової величини. Щоб одержати безрозмірну величину, її ділять на , де – середнє квадратичне відхилення випадкової величини . Одержану величину називають коефіцієнтом асиметрії випадкової величини:

. (1.35)

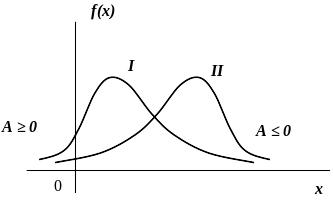
Рисунок 1.10

На рисунку 1.10 крива І має додатну (правосторонню) асиметрію ( ), а крива ІІ – від’ємну (лівосторонню) асиметрію ( ).

Ексцесом випадкової величини називається число

, (1.36)

де – четвертий центральний момент, що характеризує гостроту вершини кривої розподілу;

– середнє квадратичне відхилення випадкової величини .

Якщо для неперервної випадкової величини , то її крива розподілу має більш гостру вершину, для випадкових величин з від’ємним ексцесом характерна більш пласка вершина (рис. 1.11).

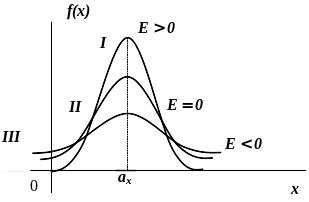
Рисунок 1.11

Приклад 1.14 Знайти коефіцієнт асиметрії та ексцес випадкової величини, розподіленої за законом Лапласа із щільністю ймовірності .