2.2 Закон розподілу Пуассона

Дискретна випадкова величина має закон розподілу Пуассона з параметром , якщо вона набуває значень 0, 1, 2, … , , … (нескінченна, але зчисленна множина) з ймовірностями

(2.5)

Ряд розподілу закону Пуассона такий:

	0	1	2	…		…
				…		…

Зрозуміло, що означення закону Пуассона є коректним, оскільки виконується основна властивість ряду розподілу:

.

Математичне сподівання та дисперсія випадкової величини, розподіленої за законом Пуассона співпадають і дорівнюють параметру його закону, тобто

(2.6)

(доведіть дане твердження самостійно).

При необмеженому збільшенні кількості випробувань ( ), за умови, що добуток прямує до параметра закону Пуассона ( ), закон Пуассона є гарним наближенням біноміального закону. В даному випадку функція ймовірностей Пуассона гарно апроксимує функцію ймовірностей, визначену за формулою Бернуллі.

При , , закон розподілу Пуассона є граничним випадком біноміального закону. Оскільки ймовірність події в кожному випробуванні мала, то закон розподілу Пуассона часто називають законом рідкісних явищ.

Приклад 2.1 Довести, що сума двох незалежних випадкових величин, розподілених за законом Пуассона з параметрами та , також розподілена за законом Пуассона з параметром .

Розв’язування

Нехай випадкові величини та розподілені за законом Пуассона з параметрами та . Оскільки дані випадкові величини незалежні, то сума набуває значення з ймовірністю

.

2.3 Рівномірний закон розподілу

Неперервна випадкова величина має рівномірний закон розподілу на відрізку , якщо її щільність ймовірності така:

(2.7)

а функція розподілу визначається за формулою:

(2.8)

Крива розподілу та графік функції розподілу випадкової величини наведено на рис. 2.1 а, б.

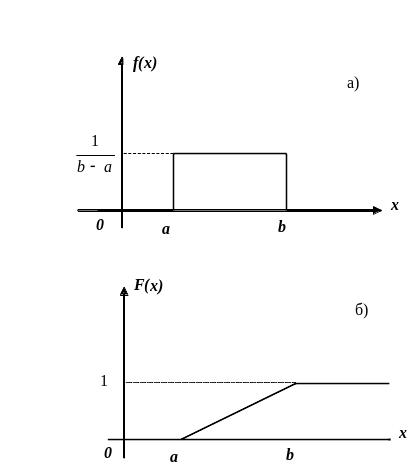
Рисунок 2.1

Теорема 2.2 Якщо випадкова величина розподілена за рівномірним законом, то її математичне сподівання

, (2.9)

а дисперсія

(2.10)

Доведення

Математичне сподівання обчислюємо за формулою:

.

Дисперсію даної випадкової величини знайдемо за формулою (1.25):

.

Рівномірний закон розподілу використовують при аналізі помилок заокруглення при проведенні числових обрахунків, в задачах масового обслуговування, при статистичному моделюванні спостережень.

Приклад 2.2 Випадкова величина Х має рівномірний розподіл із =2 і = . Знайти щільність імовірності випадкової величини Х та функцію розподілу F(x). Обчислити P(1<x<2).

Знайдемо, спочатку, параметри даного розподілу, як розв’язки системи:

, або . Звідки одержуємо дві пари розв’язків:

та . Оскільки передбачається, що , то даній умові відповідає пара . За формулами (2.7) та (2.8) маємо:

Ймовірність P(1<x<2) обчислимо за формулою (1.21):

P(1<x<2)= .

Приклад 2.3 Ціна поділки шкали вимірювального пристрою 0,2. Покази пристрою округлюються до найближчого цілого числа.

Знайти ймовірність того, що при вимірюванні буде зроблена похибка: а) менша 0,04; б) більша 0,05.