
- •Тема 1 випадкові величини
- •Поняття випадкової величини. Закон розподілу дискретної випадкової величини. Математичні операції над випадковими величинами 4
- •Тема 2 основні закони розподілу
- •Тема 3 елементи математичної статистики
- •Тема 4 розв’язування задач засобами mathcad 150
- •Тема 1 випадкові величини
- •Поняття випадкової величини. Закон розподілу дискретної випадкової величини. Математичні операції над випадковими величинами
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Математичне сподівання дискретної випадкової величини та його властивості
- •Розв’язування
- •Доведення
- •Доведення
- •Доведення
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Функція розподілу випадкової величини
- •Розв’язування
- •Доведення
- •Доведення
- •Неперервні випадкові величини. Щільність ймовірності
- •Доведення
- •Розв’язування
- •Доведення
- •Розв’язування
- •Мода, медіана, квантилі, моменти випадкових величин. Асиметрія та ексцес (надвишок)
- •Розв’язування
- •Розв’язування
- •1.7 Приклади розв’язування задач
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 2 основні закони розподілу
- •2.1 Біноміальний закон розподілу
- •Доведення
- •2.2 Закон розподілу Пуассона
- •Розв’язування
- •2.3 Рівномірний закон розподілу
- •Доведення
- •Розв’язування
- •Розв’язування
- •2.4 Показниковий закон розподілу
- •Доведення
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •2.5 Нормальний закон розподілу
- •Доведення
- •Доведення
- •Доведення
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •2.6 Розподіл
- •2.7 Розподіл Ст’юдента
- •2.8 Розподіл Фішера-Снедекора
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 3 елементи математичної статистики
- •3.1 Варіаційні ряди, їх графічне представлення та характеристики
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •3.2 Поняття оцінки параметрів. Методи знаходження оцінок
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •3.3 Статистична гіпотеза та загальна схема її перевірки
- •Розв’язування
- •1. Перевірка гіпотез про рівність середніх.
- •Розв’язування
- •2. Перевірка гіпотез про рівність дисперсій двох сукупностей.
- •Розв’язування
- •3. Побудова теоретичного закону розподілу за експериментальними даними. Перевірка гіпотез про закон розподілу
- •Розв’язування
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 4 розв’язування задач засобами MathCad
- •Розв’язання
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Словник основних математичних термінів, що зустрічаються в тексті
- •21021, М. Вінниця, Хмельницьке шосе, 95, внту
- •21021, М. Вінниця, Хмельницьке шосе, 95, внту
Тема 3 елементи математичної статистики
3.1 Варіаційні ряди, їх графічне представлення та характеристики
Встановлення статистичних закономірностей, притаманних масовим випадковим явищам, побудоване на вивченні статистичних даних – відомостей про те, які значення набула в результаті спостережень певна ознака.
Математична статистика розробляє методи отримання, математичного опису і обробки експериментальних даних, які дають змогу за результатами випробувань робити ймовірні висновки про закономірності випадкових масових явищ. Основні задачі математичної статистики такі:
оцінка невідомої функції розподілу;
оцінка невідомих параметрів розподілу;
статистична перевірка гіпотез;
довірчі інтервали.
В практиці статистичних спостережень розрізняють два види спостережень: суцільне, коли вивчаються всі об’єкти сукупності, та вибіркове, коли вивчається частина об’єктів. Прикладом суцільного спостереження є перепис населення, який охоплює усе населення країни. Вибірковим спостереженням є соціологічне опитування, яке охоплює лише частину населення країни, області, району тощо.
Уся сукупність об’єктів (спостережень), що підлягає вивченню, називається генеральною сукупністю (general aggregate). Та частина об’єктів. Що відібрана для безпосереднього вивчення генеральної сукупності називається вибірковою сукупністю або вибіркою. Кількість об’єктів у генеральній або вибірковій сукупності називають їх об’ємами.
Позначимо:
– значення ознаки (випадкової величини );
![]() – об’єми генеральної
та вибіркової сукупності;
– об’єми генеральної
та вибіркової сукупності;
![]() – число елементів
генеральної та вибіркової сукупностей
із значенням ознаки
;
– число елементів
генеральної та вибіркової сукупностей
із значенням ознаки
;
![]() – число елементів
генеральної та вибіркової сукупностей,
що мають дану ознаку.
– число елементів
генеральної та вибіркової сукупностей,
що мають дану ознаку.
Повторною
(repeatead
selection)
називають
вибірку, при якій відібраний об’єкт
(перед вибором наступного) повертається
в генеральну сукупність.
Безповторною
(non
repeatead
selection)
називають
вибірку, при якій відібраний об’єкт
не повертається в генеральну сукупність.
Репрезентативною
називають вибірку, яка вірно представляє
пропорції генеральної сукупності.
Значення ознаки
![]() окремих членів сукупності називають
варіантами, а числа, які показують,
скільки разів повторюється кожна
варіанта - частотами
окремих членів сукупності називають
варіантами, а числа, які показують,
скільки разів повторюється кожна
варіанта - частотами
![]() .
.
Приклад 3.1 Необхідно вивчити зміну виробітки на одну кравчиню швейного цеху у звітному році в порівнянні з попереднім. Отримано такі дані про розподіл 100 кравчинь цеху по ви робітці у звітному році (у відсотках до попереднього року):
 .
.
Різні значення ознаки (випадкової величини ) називають варіантами (позначають ).
Щоб скласти уявлення про дану вибірку потрібно, спочатку, її впорядкувати, розташувавши варіанти в порядку зростання (спадання). Цю операцію називають ранжуванням варіант вибірки:
![]() .
.
В такому вигляді
вивчати виробітку кравчинь також не
дуже зручно через велику кількість
числових даних. Тому розіб’ємо варіанти
на окремі інтервали, тобто проведемо
їх групування (інтервальне
групування),
суть якого полягає в наступному. Весь
розмах зміни ознаки від найменшої
![]() до найбільшої
до найбільшої
![]() розбивають на певне число інтервалів
розбивають на певне число інтервалів
![]() ,
,![]() ,
,![]() ,…,
,…,
![]() або розрядів. Число інтервалів
потрібно брати не дуже великим, щоб
після групування вибірка не була
громіздкою або дуже малою, щоб не втратити
особливостей розподілу ознаки і
підраховують частоти варіант, що
відповідно рівні
або розрядів. Число інтервалів
потрібно брати не дуже великим, щоб
після групування вибірка не була
громіздкою або дуже малою, щоб не втратити
особливостей розподілу ознаки і
підраховують частоти варіант, що
відповідно рівні
Згідно формули
Стерджеса можливе число інтервалів
![]() ,
а величина інтервалу (інтервальна
різниця, ширина інтервалу)
,
а величина інтервалу (інтервальна
різниця, ширина інтервалу)
![]() . (3.1)
. (3.1)
В прикладі 3.1
![]() .
.
Приймемо
![]() .
За початок першого інтервалу рекомендується
обирати величину
.
За початок першого інтервалу рекомендується
обирати величину
![]() .
В прикладі 3.1
.
В прикладі 3.1
![]() .
.
Наступним кроком
є підрахунок частоти
варіант
![]() ,
,![]() ,…,
,…,![]() .
Зауваження!
Числа, що
показують скільки разів зустрічаються
варіанти з даного інтервалу, називають
частотами (
.
Зауваження!
Числа, що
показують скільки разів зустрічаються
варіанти з даного інтервалу, називають
частотами (![]() ).
Відношення їх до загального числа
спостережень –
).
Відношення їх до загального числа
спостережень –
![]() називають їх вагами.
називають їх вагами.
Варіаційним рядом називають сукупність ранжованих в порядку зростання (спадання) варіант з відповідними їм вагами.
Інтервальний варіаційний ряд, або інтервальний статистичний ряд, розподілу записують у вигляді таблиці.
Таблиця 3.1
інтервал |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
В прикладі 3.1 згруповану вибірку можна подати у вигляді таблиці (табл.3.2).
Варіаційний ряд називають дискретним , якщо будь-які його варіанти відрізняються на сталу величину, та – неперервним (інтервальним) , якщо варіанти відрізняються одна від одної на як завгодно малу величину. Варіаційний ряд поданий в табл. 3.2 є інтервальним (відсотки виробітку умовно заокруглені до десятих).
Таблиця 3.2
|
Виробіток в звітному році у відсотках до попереднього |
Частота (кількість кравчинь)
|
Ваги (частка кравчинь)
|
1 |
94,0-100,0 |
3 |
0,03 |
2 |
100,0-106,0 |
7 |
0,07 |
3 |
106,0-112,0 |
11 |
0,11 |
4 |
112,0-118,0 |
20 |
0,20 |
5 |
118,0-124,0 |
28 |
0,28 |
6 |
124,0-130,0 |
19 |
0,19 |
7 |
130,0-136,0 |
10 |
0,10 |
8 |
136,0-142,0 |
2 |
0,02 |
|
|
100 |
1 |
Для задання варіаційного ряду достатньо вказати варіанти та відповідні їм частоти.
Дискретний варіаційний ряд або ряд розподілу частот може бути записаний у вигляді таблиць.
Таблиця 3.3
-


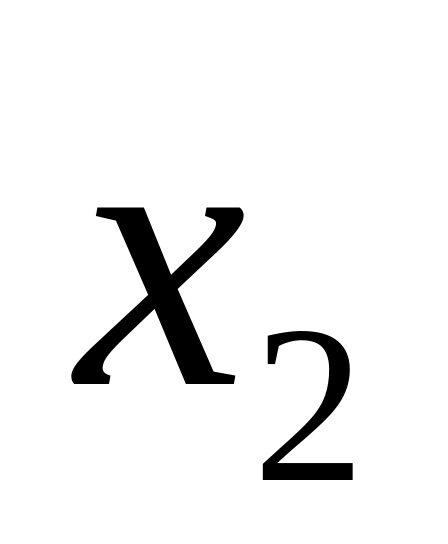
….

….
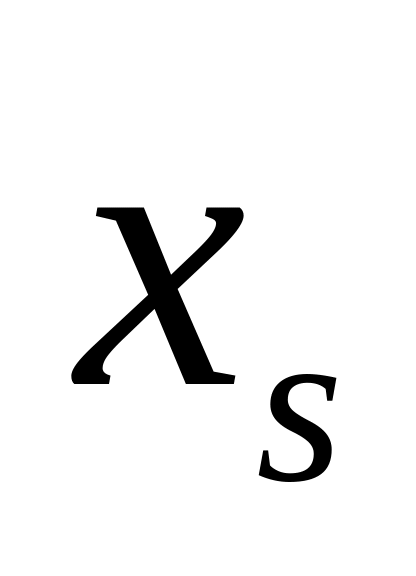
….
….
….
….
….
….
При цьому виконуються
такі рівності:
![]() ;
;![]() .
.
Прикладом дискретного ряду є розподіл 50 робітників механічного цеху по тарифному розряду (табл. 3.4).
Таблиця 3.4
Тарифний розряд |
1 |
2 |
3 |
4 |
5 |
6 |
|
Частота (кількість робітників) |
2 |
3 |
6 |
8 |
22 |
9 |
50 |
Зауваження! 1.Інтервальний ряд може бути умовно перебудований в дискретний шляхом заміни кожного інтервалу його серединою.
2. На практиці найчастіше розглядають інтервали однакової довжини .
Для графічного зображення варіаційних рядів найчастіше використовують полігон та гістограму.
Якщо на площині
нанести точки
![]() ,
,![]() ,…,
,…,![]() і
з’єднати сусідні точки відрізками
прямих ліній, то отримана ламана лінія
називається полігоном
частот або
частотним
багатокутником.
Якщо на площині нанести точки
і
з’єднати сусідні точки відрізками
прямих ліній, то отримана ламана лінія
називається полігоном
частот або
частотним
багатокутником.
Якщо на площині нанести точки
![]() ,…,
,…,![]() ,
,![]() і з’єднати сусідні точки відрізками
прямих ліній, отримаємо полігон
відносних частот.
Для побудови полігонів частот (відносних
частот) на осі абсцис відкладають
варіанти, а на вісі ординат – відповідні
їм частоти чи відносні частоти.
і з’єднати сусідні точки відрізками
прямих ліній, отримаємо полігон
відносних частот.
Для побудови полігонів частот (відносних
частот) на осі абсцис відкладають
варіанти, а на вісі ординат – відповідні
їм частоти чи відносні частоти.
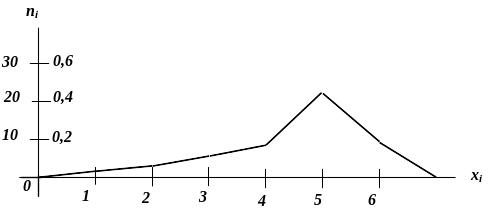
Рисунок 3.1
Гістограмою
(histogram)
називають графічне зображення
інтервального статистичного ряду
Будується гістограма так. Для кожного
частотного інтервалу довжиною
![]() знаходять суму частот варіант
знаходять суму частот варіант
![]() ,
що потрапляють в і-тий
інтервал. Вздовж осі абсцис відкладають
інтервали
,
що потрапляють в і-тий
інтервал. Вздовж осі абсцис відкладають
інтервали
![]() і на кожному з них будується прямокутник
площею
,
тобто висотою
і на кожному з них будується прямокутник
площею
,
тобто висотою
![]() .
Площа гістограми частот рівна сумі всіх
частот, тобто об’єму вибірки
.
.
Площа гістограми частот рівна сумі всіх
частот, тобто об’єму вибірки
.
Для побудови
гістограми відносних частот на осі
абсцис відкладають часткові інтервали
і на кожному з них будується прямокутник
висотою
![]() .
Площа гістограми відносних частот рівна
сумі всіх відносних частот, тобто
одиниці.
.
Площа гістограми відносних частот рівна
сумі всіх відносних частот, тобто
одиниці.
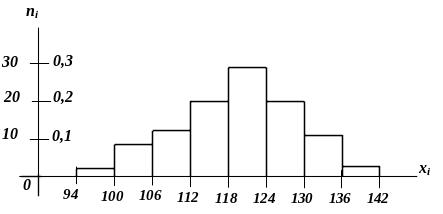
Рисунок 3.2
Надзвичайно
важливим є поняття емпіричної та
теоретичної функцій розподілу. Функцію
розподілу
![]() генеральної сукупності називають
теоретичною
функцією розподілу.
Емпіричною
функцією розподілу (empiric
function
of
distribution)
(функцією розподілу вибірки)
називають функцію
генеральної сукупності називають
теоретичною
функцією розподілу.
Емпіричною
функцією розподілу (empiric
function
of
distribution)
(функцією розподілу вибірки)
називають функцію
![]() ,
яка визначає для кожного значення
відносну частоту події
.
,
яка визначає для кожного значення
відносну частоту події
.
![]() , (3.2)
, (3.2)
де
![]() -
число тих
-
число тих
![]() ,
для яких
,
для яких
![]() ;
-
об’єм вибірки. При великих
;
-
об’єм вибірки. При великих
![]() або
або
![]()
![]() .
.
Вкажемо основні властивості емпіричної функції розподілу:
значення емпіричної функції належать проміжку
 ;
;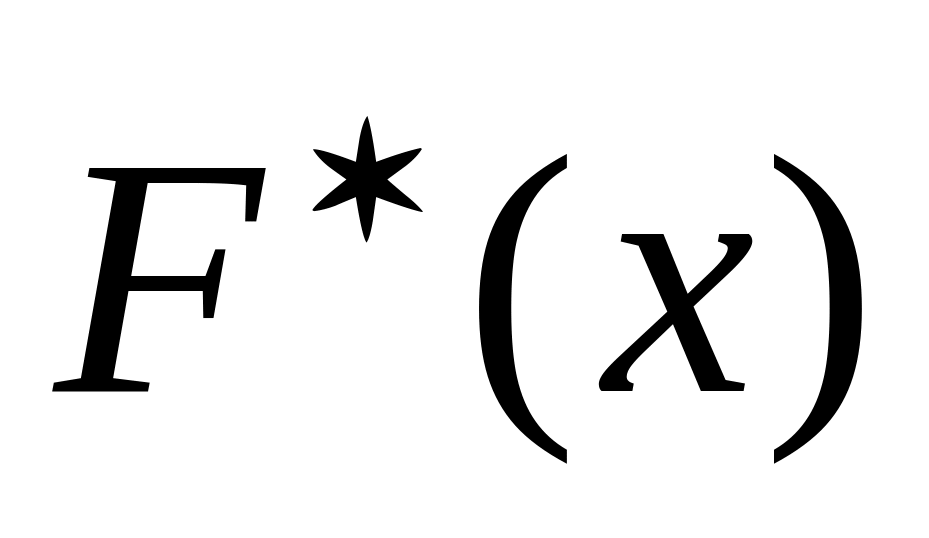 -
неспадна функція;
-
неспадна функція;якщо
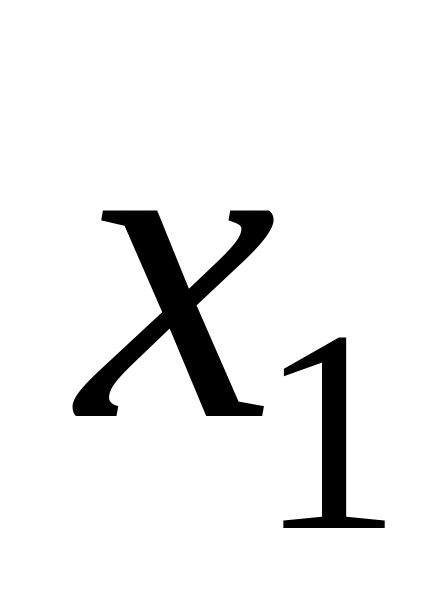 і
і
 -
відповідно найменша і найбільша
варіанти, то
-
відповідно найменша і найбільша
варіанти, то
 при
при
 і
і
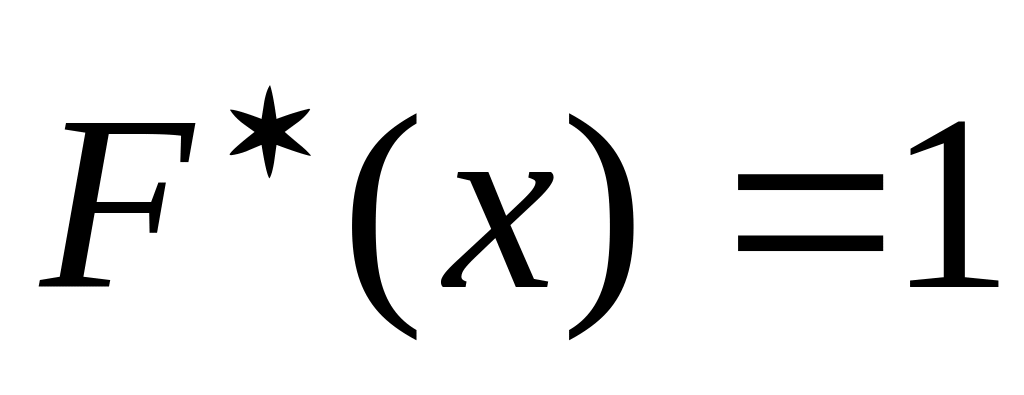 при
при
 .
.
Графік емпіричної
функції для дискретного варіаційного
ряду – східчаста лінія, яка має розриви
(скачки) в точках
,
![]() і т.д. Для інтервального варіаційного
ряду маємо лише значення функції
розподілу на кінцях інтервалу. Тому для
графічного подання такої функції
доцільно її до визначити, з’єднавши
точки графіку, що відповідають кінцям
інтервалів, відрізками прямої.
і т.д. Для інтервального варіаційного
ряду маємо лише значення функції
розподілу на кінцях інтервалу. Тому для
графічного подання такої функції
доцільно її до визначити, з’єднавши
точки графіку, що відповідають кінцям
інтервалів, відрізками прямої.
Розглянемо основні характеристики варіаційного ряду.
Значення ознаки
(варіанти), яке розділяє ранжований
варіаційний ряд на дві рівні за кількістю
варіант частини називається медіаною
![]() .
.
Якщо число варіант
парне, тобто
![]() ,
то
,
то
![]() ,
при непарному
,
при непарному
![]()
![]() .
З означення емпіричної інтегральної
функції випливає рівність
.
З означення емпіричної інтегральної
функції випливає рівність
![]() .
Для інтервального ряду виходячи з умови
.
Для інтервального ряду виходячи з умови
![]() і
і
![]() знаходять медіанний інтервал
знаходять медіанний інтервал
![]() .
Тоді, використовуючи лінійну інтерполяцію,
значення медіани на цьому інтервалі
обчислюють згідно формули:
.
Тоді, використовуючи лінійну інтерполяцію,
значення медіани на цьому інтервалі
обчислюють згідно формули:
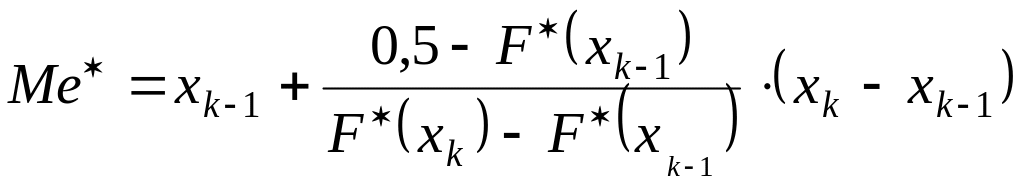 . (3.3)
. (3.3)
Для знаходження медіани можна використати іншу формулу:
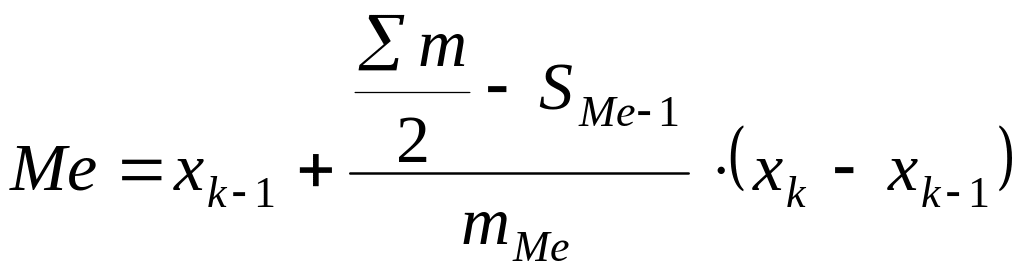 , (3.4)
, (3.4)
де![]() -
сума всіх частот;
-
сума всіх частот;
![]() -
сума частот до медіанного інтервалу;
-
сума частот до медіанного інтервалу;
![]() -
частота медіанного інтервалу.
-
частота медіанного інтервалу.
Для того, щоб знайти
медіанний інтервал, послідовно знаходять
нагромаджені частоти
![]() .
Першій нагромадженій частоті
.
Першій нагромадженій частоті
![]() ,
яка більша за
,
яка більша за
![]() ,
відповідає медіанний інтервал (у випадку
дискретного ряду
відповідає самій медіані).
,
відповідає медіанний інтервал (у випадку
дискретного ряду
відповідає самій медіані).
Модою
![]() дискретного
статистичного розподілу називається
варіанта, що має найбільшу частоту. Для
інтервального розподілу визначається
модальний інтервал
,
якому відповідає найбільша щільність
відносної частоти
дискретного
статистичного розподілу називається
варіанта, що має найбільшу частоту. Для
інтервального розподілу визначається
модальний інтервал
,
якому відповідає найбільша щільність
відносної частоти
![]() ,
де
-
число варіант з
-того
інтервалу. Тоді згідно лінійної
інтерполяції значення
всередині модального інтервалу рівне:
,
де
-
число варіант з
-того
інтервалу. Тоді згідно лінійної
інтерполяції значення
всередині модального інтервалу рівне:
![]()
![]() , (3.5)
, (3.5)
де
![]() -
початок модального інтервалу, тобто
інтервалу, в якому міститься мода;
-
початок модального інтервалу, тобто
інтервалу, в якому міститься мода;
![]() -
частота інтервалу попереднього перед
-
частота інтервалу попереднього перед
![]() (що передує модальному);
(що передує модальному);
![]() -
частота модального інтервалу;
-
частота модального інтервалу;
![]() -
частота інтервалу наступного за
модальним.
-
частота інтервалу наступного за
модальним.
Розмахом
варіації
![]() називають різницю між найбільшою і
найменшою варіантами:
називають різницю між найбільшою і
найменшою варіантами:
![]() .
.
Середнім
вибірковим
(арифметичним)
варіаційного ряду називається дріб, в
чисельнику якого міститься сума добутків
варіант
ряду на відповідні їм ваги
![]() ,
а в знаменнику – сума ваг, тобто об’єм
вибірки
:
,
а в знаменнику – сума ваг, тобто об’єм
вибірки
:
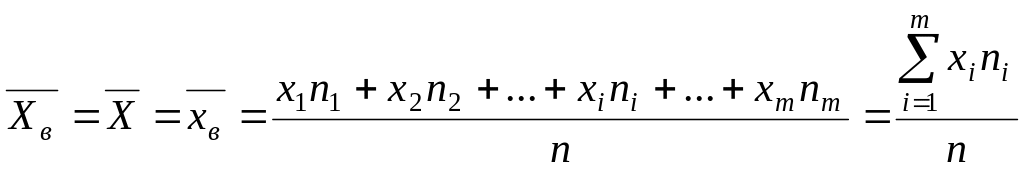 . (3.6)
. (3.6)
За середню арифметичну неперервного варіаційного ряду приймають середню арифметичну дискретного розподілу, що відповідає даному неперервному. Це означає, що частоти неперервного розподілу відносять до середин відповідних інтервалів, які тепер стають варіантами.
Приклад 3.2 Знайти середню виробітку кравчинь за даними таблиці 3.2
