2. Математичне сподівання дискретної випадкової величини та його властивості

Розглянемо таку задачу. Відомі закони розподілу випадкових величин та – кількість очок, що набрав 1-ий та 2-ий стрілок відповідно.

:

	0	1	2	3	4	5	6	7	8	9	10
	0,15	0,11	0,04	0,05	0,04	0,1	0,1	0,04	0,05	0,12	0,2

:

	0	1	2	3	4	5	6	7	8	9	10
	0,01	0,03	0,05	0,09	0,11	0,24	0,21	0,1	0,1	0,04	0,02

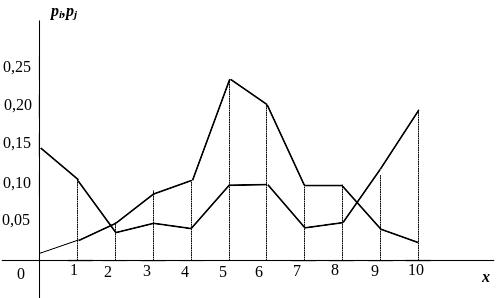Потрібно з’ясувати, котрий з двох стрілків стріляє краще. Розглянувши ряди розподілу випадкових величин та важко відповісти на це запитання через велику кількість значень. До того ж в першого стрілка достатньо великі ймовірності мають крайні значення кількості очок ( =0; 1 та =9; 10), а в другого стрілка – середні значення (див. полігон розподілу ймовірностей та на рис. 1.3)

Рисунок 1.3

Зрозуміло, що з двох стрілків краще стріляє той, хто в середньому набирає більшу кількість очок. Таким середнім значенням випадкової величини є її математичне сподівання.

Математичним сподіванням (mathematical hope) дискретної випадкової величини називають суму добутків усіх її значень на відповідні їм ймовірності:

. (1.3)

Приклад 1.4 Обчислити та в задачі про стрілків.

Розв’язування

За формулою (1.3) маємо:

;

.

З механічної точки зору математичне сподівання є абсциса центру мас системи матеріальних точок з абсцисами та масами .

Розглянемо основні властивості математичного сподівання.

1. Математичне сподівання сталої величини є величина стала:

, де . (1.4)

Доведення

Сталу величину можна розглядати як величину, що приймає значення з ймовірністю 1. Тому .

2. Сталий множник можна виносити за знак математичного сподівання, тобто:

, де . (1.5)

Доведення

Дійсно .

3. Математичне сподівання алгебраїчної суми скінченої кількості випадкових величин дорівнює алгебраїчній сумі математичних сподівань, тобто:

. (1.6)

Доведення

Згідно означенню операції додавання (віднімання) випадкових величин маємо:

.

Оскільки в першій подвійній сумі не залежить від індексу , а в другій сумі не залежить від індексу , то

.

4. Математичне сподівання добутку скінченного числа випадкових величин дорівнює добутку їх математичних сподівань:

. (1.7)

5. Якщо всі значення випадкової величини збільшити (зменшити) на сталу , то на цю ж сталу збільшиться (зменшиться) математичне сподівання цієї випадкової величини:

. (1.8)

Доведення

Враховуючи властивості 1 та 3 математичного сподівання, одержуємо

.

6. Математичне сподівання відхилення випадкової величини від її математичного сподівання дорівнює нулю:

. (1.9)

Доведення

Нехай , тоді використавши властивість 5 одержуємо

.

Приклад 1.5 Знайти математичне сподівання випадкової величини , якщо відомо, що , .

Розв’язування

Використовуючи властивості 1, 2, 3 математичного сподівання знаходимо

.

3. Дисперсія дискретної випадкової величини

Тільки математичне сподівання не може в достатній мірі охарактеризувати випадкову величину. В задачі про стрілків (п. 1.2) ми переконались, що , тобто середня кількість очок у обох стрілків однакова. Зрозуміло, що краще стріляє той стрілок, в якого менше відхилення кількості очок відносно середнього значення.

Дисперсією (dispersion) випадкової величини називається математичне сподівання квадрата її відхилення від математичного сподівання:

. (1.10)

Якщо випадкова величина – дискретна із скінченною кількістю значень, то

. (1.11)

З формули (1.11) випливає, що дисперсія має розмірність квадрату, що не завжди зручно. Тому в якості показника ступеня розсіювання використовують також величину .

Середнім квадратичним відхиленням (standard deviation) випадкової величини називається арифметичне значення кореня квадратного з її дисперсії:

. (1.12)

Приклад 1.6 В задачі про стрілків (п. 1.2) обчислити дисперсію та середнє квадратичне відхилення кількості одержаних очок для кожного стрілка.