17.4. Магнітне поля прямолінійного провідника зі струмом

Знайдемо вектор магнітної індукції в точці A, що відстоїть від прямолінійного провідника зі струмом на відстані R. Для цього скористаємося законом Біо–Савара–Лапласа (17.16). Для обчислення інтеграла (17.16) виразимо змінні r і dl через .

Згідно з рис. 17.4 маємо

; .

(17.18)

Рис. 17.4

Продиференціюємо останню рівність

(17.19)

За допомогою (17.18) і (17.19) підінтегральний вираз в (17.16) можна перетворити до вигляду

.

Підставимо здобутий вираз у формулу (17.16) і зінтегруємо у межах від  ₁ до ₂ (рис. 17.4).

(17.20)

Формула (17.20) застосовна для провідника скінченої довжини. Для нескінченно довгого провідника слід покласти ₁ = ,  ₂ = . Тоді з (17.20) випливає

(17.21)

17.5. Магнітне поле кругового струму

Нехай по провіднику у вигляді тонкого кільця радіуса a протікає струм I. Знайдемо вектор магнітної індукції в точці A, розміщеній на осі кільця й віддаленої від його центра на відстань R (рис. 17.5).

Виділимо на кільці елемент струму Idl. У точці A він створює вектор магнітної індукції . Розкладемо на дві складові:

.

Перпендикулярна складова не дає ніякого внеску в загальну індукцію в точці A, оскільки на кільці завжди найдеться симетрично розташований елемент струму Idl, що дає протилежно напрямлену складову .

Рис. 17.5

З рис. 17.5 видно, що

.

Оскільки , то sin  = 1, отже,

;

.

Інтегруючи за всім контуром, дістанемо:

,

,

де S – площа, охоплена круговим струмом.

Добуток сили струму I на площу, обмежену круговим струмом, називається магнітним моментом кругового струму (витка):

,

(17.22)

Рис. 17.6

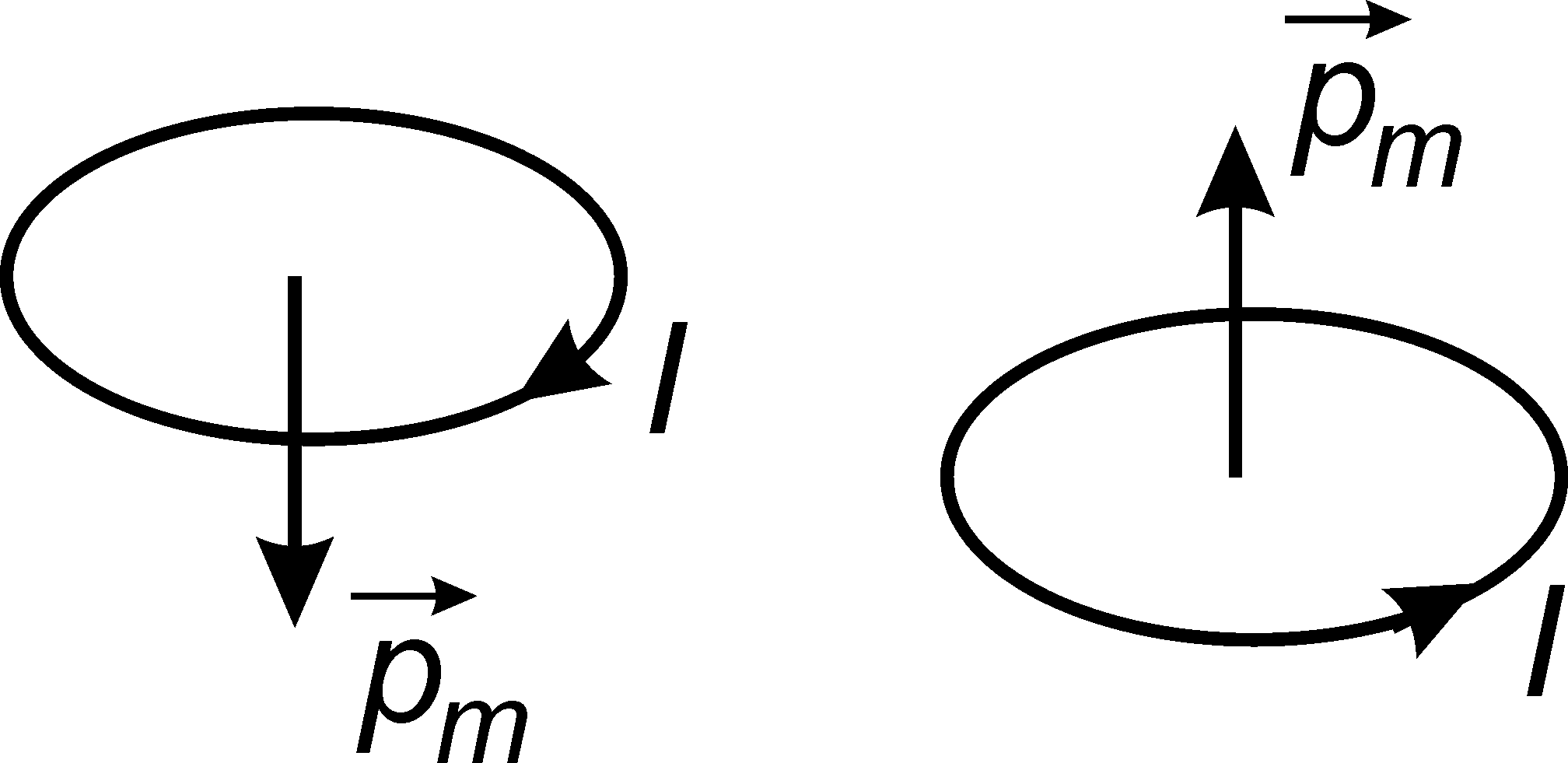
де  – одиничний вектор, перпендикулярний до площини витка зі струмом. Напрямок знаходиться за правилом правого гвинта (рис. 17.6).

Таким чином, модуль вектора магнітної індукції на осі кругового струму

.

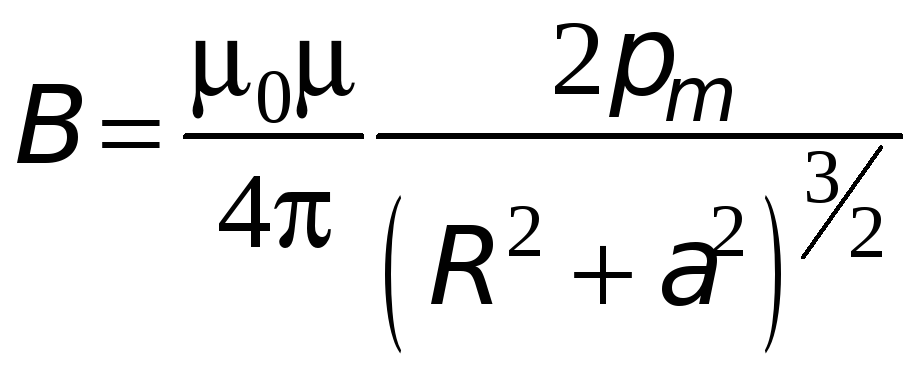(17.23)

При R>>a з (17.23) випливає

.

(17.24)

Зіставляючи (17.24) і (11.9), доходимо висновку, що круговий виток зі струмом створює магнітне поле, що, як і електричне поле диполя, на великих відстанях убуває як 1/R³.

В центрі кругового витка (R=0) з формули (17.23) дістанемо

.

Оскільки p_m=IS=Ia², то

.

(17.25)

17.6. Циркуляція вектора

В електростатиці було показано, що циркуляція вектора напруженості електростатичного поля дорівнює нулю (див. §11.6). Цей результат свідчить про потенціальний характер електростатичного поля.

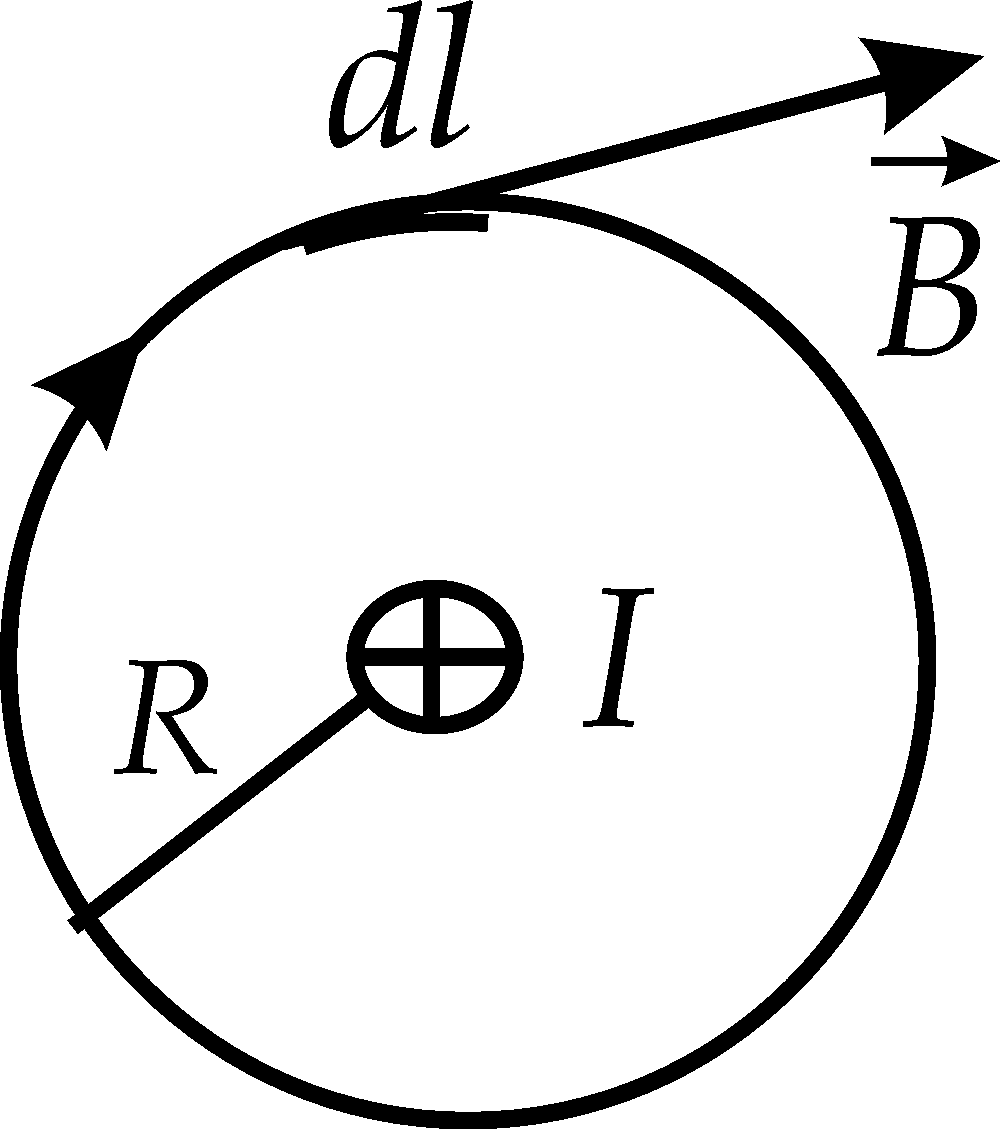
Рис. 17.7

З'ясуємо тепер, чому дорівнює циркуляція вектора магнітної індукції . Розглянемо найпростіший випадок, коли магнітне поле створюється нескінченним прямолінійним провідником, а контур інтегрування збігається з лінією індукції. Тоді вираз для циркуляції вектора з врахуванням (17.21) буде мати вигляд

.

(17.26)

Підставляючи в (17.26) значення з (17.21) і з огляду на те, що , дістанемо

.

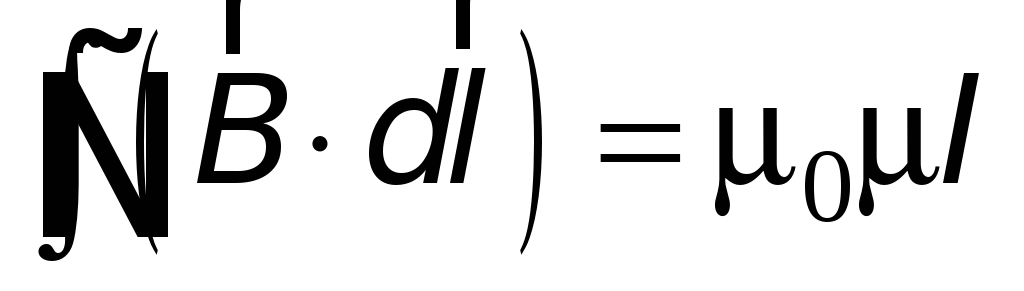(17.27)

Вираз (17.27) можна узагальнити на випадок, коли контур має довільну форму й охоплює кілька провідників зі струмом:

.

(17.28)

Знак "+" у формулі (17.28) вибираємо в тому випадку, якщо напрямок струму й напрямок обходу задовольняють правилу лівого гвинта, і "–" – у противному випадку.

Як видно з (17.28), циркуляція вектора магнітної індукції відмінна від нуля. Це означає, що магнітне поле має непотенціальний характер – для нього не можна ввести поняття потенціалу. Магнітне поле є вихровим.

Якщо врахувати, що B= ₀H, то з (17.28) можна дістати вираз для циркуляції вектора напруженості магнітного поля:

.

(17.29)

Останню формулу називають іноді законом повного струму: циркуляція вектора напруженості магнітного поля дорівнює алгебраїчній сумі струмів, що містяться всередині даного контуру.

Формули (17.28) і (17.29) застосовують для розрахунку магнітних полів. У деяких випадках такий розрахунок значно простіший, ніж заснований на законі Біо-Савара-Лапласа.