14.2. Енергія зарядженого провідника

Заряд, розташований на поверхні провідника, можна розглядати як систему точкових зарядів, тому для обчислення енергії зарядженого провідника можна скористатися формулою (14.4). Потенціал будь-якої точки поверхні провідника однаковий (_i=), оскільки його поверхня еквіпотенціальна. Отже, у формулі (14.4) потенціал можна винести за знак суми:

або

,

(14.5)

де – заряд провідника.

З врахуванням (13.3) вираз для енергії зарядженого провідника можна представити у вигляді

(14.6)

або

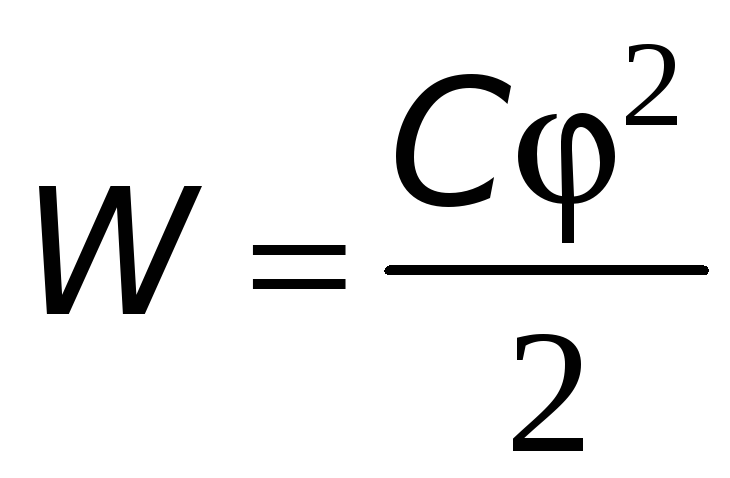
(14.7)

14.3. Енергія зарядженого конденсатора. Густина енергії електростатичного поля

Для обчислення енергії зарядженого конденсатора скористаємося формулами (14.5) – (14.7), замінивши  на різницю потенціалів між обкладками конденсатора U=__. Тоді

,	(14.8)
	(14.9)
	(14.10)

Подальший розгляд проведемо, ґрунтуючись на формулі (14.9). Представимо заряд конденсатора як Q=S, де  – поверхнева густина заряду, а S – площа обкладки конденсатора. Скориставшись далі виразом для ємності плоского конденсатора (13.7), представимо (14.9) у вигляді

,

(14.11)

де V=Sd – об'єм конденсатора.

За допомогою (11.15) виразимо поверхневу густину заряду  через напруженість поля E і підставимо здобутий вираз в (14.11). У результаті дістанемо

,

(14.12)

У формулі (14.9) енергія зарядженого конденсатора виражена через заряд на його обкладках і ємність. У формулі (14.12) енергія конденсатора виражена через напруженість електростатичного поля, зосередженого між його обкладками. У зв'язку із цим виникає принципове питання про те, що служить носієм енергії конденсатора: заряди чи електростатичне поле. Це питання – центральне у тривалій дискусії між прихильниками далеко- та близькодії.

Прихильники далекодії віддавали перевагу формулі (14.9), розглядаючи її як потенціальну енергію взаємодії двох тіл. Прихильники цієї теорії відкидали можливість здійснення взаємодії за допомогою поля.

Прихильники теорії близькодії (польової теорії) вважали, що енергія конденсатора є енергія електростатичного поля (формула (14.2)). Ця енергія "розмазана" по всьому об'ємі конденсатора й, отже, можна говорити про об'ємну густину енергії:

[Дж/м³]

або

,

(14.13)

З врахуванням (12.11) формулу (14.13) можна представити у вигляді

(14.14)

У рамках електростатики вирішити питання, що є носієм енергії – заряди чи поле, неможливо, оскільки нерухомі заряди й створюване ними електростатичне поле невіддільні один від одного. При вивченні змінних електричних і магнітних полів виявилося, що електромагнітне поле може відриватися від зарядів, існуючи незалежно від них. Це і є вирішальний аргумент на користь теорії близькодії (польової теорії).

15. Постійний електричний струм

15.1. Сила та густина струму

Електричним струмом називають упорядкований (спрямований) рух заряджених мікрочастинок або заряджених макроскопічних тел. За напрямок струму приймають напрямок руху позитивних зарядів; якщо струм створюється негативно зарядженими частинками (наприклад, електронами), то напрямок струму протилежний напрямку руху частинок. Розрізняють струм провідності (спрямований рух заряджених часток усередині макроскопічного тіла) і конвекційний (рух зарядженого тіла як цілого). Надалі будемо розглядати лише струм провідності.

Кількісно електричний струм характеризується скалярною величиною силою струму I і векторною величиною – густиною електричного струму .

Сила струму чисельно дорівнює заряду, що пройшов через поперечний переріз провідника за одиницю часу:

.

(15.1)

Сила струму вимірюється в амперах (визначення дане у вступі).

На різних ділянках поперечного перерізу провідника за один і той же час може протікати різний по величині заряд. Для врахування цієї обставини вводять поняття вектора густини струму. Вектор густини струму чисельно дорівнює силі струму, що протікає через одиничний поперечний переріз провідника:

[А/м2],

(15.2)

де знак "" позначає, що площадка орієнтована перпендикулярно до напрямку струму. Напрямок вектора збігається з напрямком руху позитивних зарядів.

Знайдемо вираз для вектора густини струму в металах, у яких носіями струму є вільні електрони. Під дією електричного поля електрони в металі рухаються спрямовано із середньою швидкістю . За одиницю часу через одиничну площадку поперечного переріза провідника пройде n електронів, де n – число електронів в одиниці об'єму (концентрація). При цьому буде перенесений заряд en . Отже густина струму

.

(15.3)