3.1.8. Функция Эйлера

Количество классов вычетов в приведенной системе вычетов обозначают через (т) и называют функцией Эйлера. Она определена для всех натуральных чисел и представляет собой количество чисел ряда 0,1,…, т, взаимно простых с т.

Примеры. (1) = 1, (2) = 1, (3) = 2, (4) = 2, (5) = 4,  (6) = 2.

Очевидны следующие свойства (р — простое).

Свойство 1. (р)=р-1.

Свойство 2. (р^k)= р^k – р^k-1, kN.

Лемма 1. (мультипликативность функции Эйлера).

(a,b)=1 => (ab)= (a) (b).

Используя лемму и каноническое разложение числа на простые множители

имеем

Теорема 1 (Ферма), а^р-1l(mod р), если (а,р) =1.

Теорема 2 (Эйлер), а^(т)l(mod т), если (а,т) =1.

3.1.9. Сравнения первой степени

Рассмотрим сравнение

aх b(mod m) (1)

при условии (а,т) =1. Под решением любого сравнения понимают класс вычетов по модулю т, один элемент которого (а значит, и все) удовлетворяет срав­нению. В нашем случае найдутся целые и, v такие, что аи + mv = 1. Следователь­но, аи l(mod т). Будем называть и обратным к а по модулю т. Умножим обе части сравнения 1 на и. Получим

x=bu(mod m). (2)

Следовательно, сравнение имеет единственное решение по модулю т.

Пусть (а,т)=d > 1. По свойству 10 условие d|b является необходимым условием разрешимости сравнения 1. Будем считать его выполненным. Пусть a=a₁d, b=b₁d, m=m₁d. Тогда наше сравнение равносильно а₁х = =b₁(modm₁). Имеем одно решение х  x₁(mod m₁). По модулю т имеем d реше­ний:

х₁, х₁ + т₁, х₁ + 2m₁,...,х₁ + (d -1)m₁.

Теорема 1. Пусть (а,т) = d. Сравнение ax =b(mod m) разрешимо тогда

и только тогда, когда d|b. В этом случае оно имеет d решений.

При небольшом т сравнение ax b(mod m) решается подбором. Для этого достаточно найти число и такое, что аи l(mod m); это можно сделать с помощью алгоритма Евклида. В качестве и можно также взять

u = а^(т)-1(способ Эйлера).

3.1.10. Система сравнений первой степени

Система сравнений

a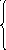₁х  b₁(mod m₁);

a₂x  b₂(mod m₂);

… (3.1.10.1)

a_nx  b_n(mod m_n)

сводится к системе

х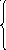  b₁(mod m₁);

x  b₂(mod m₂); (3.1.10.2)

…

x  b_n(mod m_n).

Для решения последней достаточно уметь решать систему

х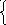  b₁(mod m₁);

x  b₂(mod m₂). (3.1.10.3)

Система (3.1.10.3) в случае ее разрешимости имеет единственное решение по модулю [т₁,т₂]. Исходная система (3.1.10.1) в случае ее разрешимости имеет единственное решение по модулю [т₁,т₂, ...,т_n].

В случае, когда все модули т₁,т₂, ...,m_n попарно взаимно простые, к системе (3.1.10.2) применим так называемый китайский способ. Определим числа х₁,х₂, ...,х_п из условий т₂т₃ ...m_nx₁ l(mod т₁), т₁т₃ ...m_nх₂ 1(mod т₂), …, т₁т₂ ...m_n-1х_п1 (mod т_т). Тогда решением системы (3.1.10.2) будет число

х= т₂т₃ ...m_nx₁b₁ + т₁т₃ ...m_nx₂b₂ + ...+ т₁т₂ ...m_n-1x_пb_п.

Теорема (китайская теорема об остатках). Система сравнений (3.1.10.2) при попарно взаимно простых модулях имеет единственное решение по модулю произведения.