2. Примеры поточных шифрсистем

Шифрсистема А5

А5 – шифрсистема гаммирования, применяемая для шифрования телефонных сеансов в европейской системе мобильной цифровой связи GSM (Group Special Mobile). В открытой печати криптосхема А5 официально не публиковалась. Британская телефонная компания передала всю техническую документацию Брэдфордскому университету. Через некоторое время детали о конструкции А5 стали просачиваться в печать и, в конце концов, появились в INTERNET. Описание алгоритма приведено в работе.

В системах GSM алгоритм А5 используется для защиты информации между абонентом и базовой станцией, так что фактически в сеансе связи двух абонентов шифрование происходит дважды. Это дает возможность использования атаки на основе известного открытого текста. Кроме того, следует отметить, что 64-битовый секретный сеансовый ключ (которым служит совокупность начальных заполнений ЛРС) генерируется с помощью другого алгоритма, исходя из "основного" (master) ключа, специфического для каждого пользователя, и открытого случайного 128-битового ключа, передаваемого в незащищенной форме с базовой станции абоненту. Тем самым успешное вскрытие одного или нескольких сеансовых ключей дает подходы к определению основного ключа пользователя.

Шифрсистема Гиффорда

Д. Гиффорд предложил схему поточного шифра, которая использовалась с 1984 по 1988 г. агентством Associated Press. Криптосхема генератора представляет 8-байтовый регистр сдвига с линейной функцией обратной связи f и нелинейной функцией выхода h. Ключом являются 64 бита начального заполнения регистра. Схема реализует шифр гаммирования.

В 1994 г. Кейном и Шерманом был предложен метод определения ключа данной криптосхемы, использующий память объема 2¹⁸ бит и имеющий сложность 2²⁷ элементарных операций, что существенно меньше сложности тотального перебора всех 2⁶⁴ начальных состояний. Программа, реализующая данный метод на сети из 8 станций Sparс, находила ключ по одному шифрованному сообщению достаточной длины среднем за 4 часа.

5.3. Линейные регистры сдвига

Широкое распространение в криптографических приложениях линейных регистров сдвига над конечными полями и кольцами обусловлено целым рядом факторов. Среди них можно отметить:

– пользование только простейших операций сложения и умножения, аппаратно реализованных практически на всех вычислительных средствах;

– высокое быстродействие создаваемых на их основе криптографических алгоритмов;

– большое количество теоретических исследований свойств рекуррентных последовательностей (ЛРП), свидетельствующих об их удовлетворительных криптографических свойствах.

Введем ряд определений.

Последовательностью над полем Р будем называть любую функцию и:n₀—>Р, заданную на множестве целых неотрицательных чисел и принимающую значения в поле.

Последовательность и называют линейной рекуррентной последовательностью (ЛРП) порядка т>0 над полем Р, если существуют константы f₀,...,f_{т -1} P такие, что

u(i+m)=

ЛРП реализуется схемой линейного регистра сдвига.

В очередном такте работы регистра значения, содержащиеся в ячейках его накопителя, умножаются на соответствующие коэффициенты (f_j) и суммируются, после чего происходит (левый) сдвиг информации в регистре, а в освободившуюся крайнюю ячейку записывается вычисленное значение суммы. Заметим при этом, что операции сложения и умножения выполняются в поле Р.

Равенство, выражающее зависимость между знаками линейной рекуррентной последовательности, называют законом рекурсии, многочлен

характеристическим многочленом ЛРП и, а вектор

и=(u(0),...,u(m – 1)) – начальным вектором ЛРП (или начальным заполнением ЛРС).

Характеристический многочлен ЛРП и, имеющий наименьшую степень, называется ее минимальным многочленом, а степень минимального многочлена – линейной сложностью ЛПР и.

Линейная сложность ЛРП определяет минимальную длину линейного регистра сдвига, реализующего данную последовательность.

Периодом последовательности и называется наименьшее натуральное число t, для которого существует натуральное число  > 0 такое, что для всех i >0 справедливо равенство u(+i+t)=u( +i).

Из вида закона рекурсии следует, что в случае, когда Р – конечное поле из q элементов, максимальное значение периода ЛРП порядка т равно q^m –1. В самом деле, нулевой начальный вектор порождает последовательность, состоящую из одних нулей, а число различных заполнений регистра длины т равно q^m.

Последовательности, имеющие максимально возможный период, получили название линейных рекуррентных последовательностей максимального периода или просто максимальныx рекуррентных последовательностей.

Значения периодов линейных рекуррентных последовательностей определяются свойствами их минимальных многочленов. В частности, для того чтобы линейная рекуррентная последовательность порядка т над полем из q элементов имела максимальный период, необходимо и достаточно, чтобы минимальный многочлен был примитивным многочленом. Так называется неприводимый многочлен, корень которого имеет в мультипликативной группе поля разложения порядок q^m –1.

Несмотря на то, что имеется достаточно много критериев проверки неприводимости многочленов над конечными полями и методов их построения, доказать то, что заданный неприводимый многочлен примитивен, удается в исключительных случаях.

Для конечного поля из q элементов будем использовать стандартное обозначение GF(q) .

Утверждение 1.Если F(x) – неприводимый многочлен над полем GF(2) степени т, и 2^m –1 – простое число, то F(x) – примитивный многочлен.

Общий подход к построению примитивных многочленов состоит в построении неприводимых многочленов и непосредственном вычислении их периодов. Проверка максимальности периода неприводимого многочлена может быть осуществлена с помощью следующего утверждения:

Утверждение 2. Неприводимый многочлен F(x) примитивен в том и только в том случае, когда для любого простого числа р , делящего q^m – 1, многочлен не сравним с 1 по модулю многочлена F(x).

Построение примитивных многочленов представляет собой сложную задачу, решение которой даже в частных случаям сопряжено со значительными трудностями вычислительного характера. На практике используются таблицы неприводимых и примитивных многочленов над конечными полями.

Закон рекурсии дает удобный способ вычисления очередного знака ЛРП через предыдущие, но при изучении ее свойств более предпочтительной формой задания является формула общего члена последовательности, представляющая собой аналитическое выражение члена последовательности в виде функции от его номера. Рассмотрим этот способ представления на примере ЛРП над конечными полями с неприводимыми характеристическими многочленами.

Пусть P=GF(q) и Q – поле из q ^m элементов, являющееся расширением поля Р. Тогда функцией "след" из поля Q в поле Р называется отображение

вида

В силу свойств конечных полей справедливы равенства

означающие, что функция "след" является линейным отображением над полем Р.

лемма 1. Для любого ненулевого а  Р и любого b Р число решений уравнения равно q^m-1.

Теорема 1. Пусть – неприводимый многочлен над

полем Р степени т,  —корень F(x) в поле Q. Тогда для ЛРП {u(i)} с характеристическим многочленом F(x) существует единственная константа а  Р, такая, что

Пусть и – ЛРП максимального периода над полем Р и

v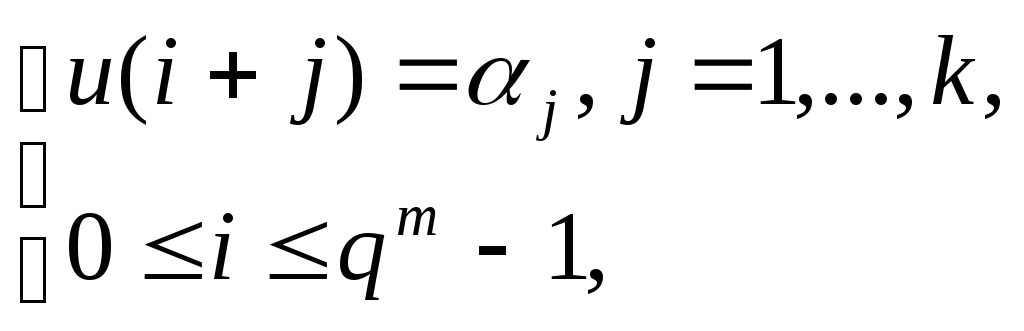(₁,…,_k) — число решений системы уравнений

то-есть число появлений мультиграммы ₁,…,_k на периоде последовательности и.

Утверждение 3. Пусть F(x) – примитивный многочлен степени т над полем Р и  – корень F(x) в поле Q. Тогда любая ненулевая мультиграмма (₁,…,_k) встречается на периоде ЛРП и ровно

v(₁,…,_k)=q^m-k

раз, а число вхождений нулевой мультиграммы на единицу меньше.

Представленные результаты показывают, что линейные рекуррентные последовательности над полем позволяют обеспечить первые два из трех требований к псевдослучайным последовательностям, используемым при построении управляющих блоков поточных шифрсистем. За счет выбора закона рекурсии можно гарантировать достаточную величину периода получаемой псевдослучайной последовательности и хорошие статистические качества. В самом деле, ее период совпадает с числом всех ненулевых векторов длины, равной степени минимального многочлена ЛРП, и каждый из этих векторов встречается на периоде последовательности в точности один раз.

Вместе с тем аналитическое строение ЛРП оказывается очень простым. Для определения начального вектора по некоторому отрезку последовательности достаточно решить несложную систему линейных уравнений. Поэтому при использовании линейных регистров сдвига в криптографических приложениях необходимо предусматривать процедуры, повышающие сложность аналитического строения вырабатываемых ими рекуррентных последовательностей.