3.2.4. Гомоморфизмы групп

Отображение f: G  G группы G в группу G называется гомоморфизмом, если оно согласовано с операциями на группах G и G', т.е. f(ab) = f(a)f(b) для любых двух элементов a,b G. Если это отображение сюръективное, то оно называется эпиморфизмом. В этом случае группа G' называется гомоморфным образом группы G. Приставка «моно» употребляется в случае, когда гомоморфизм инъективен. Биективный гомоморфизм называется изоморфизмом. Для изоморфных групп употребляется обозначение G Н. Изоморфизм группы G на себя называется автоморфизмом.

Примеры. Обозначим через GL(n, R) группу по умножению всех невырож-енных матриц п-го порядка с вещественными элементами. Тогда отображение Аdet A, AGL(n, R) будет эпиморфизмом на мультипликативную группу поля вещественных чисел R*.

Еще один пример эпиморфизма дает отображение : Z  Z_т, при котором (а)= а, т.е. элемент a  Z отображается в соответствующий класс вычетов по модулю т.

Ядром гомоморфизма f: G  H называется множество

ker f = {aG|f(a)=e'},

где e'— единичный элемент группы H.

В случае гомоморфизма GL(n,R)  R* ядром будет подгруппа матриц с единичным определителем. Ядром во втором примере является группа чисел тZ, кратных модулю т.

Сохранив для аддитивной группы поля вещественных чисел обозначение R и обозначив через R⁺ мультипликативную группу положительных вещественных чисел, имеем изоморфизм R⁺ R, заданный функцией у = ln x.

Легко показать, что ядро любого гомоморфизма является подгруппой H группы G c важным дополнительным условием: g^-1Hg = H для любого элемента gG. Такие подгруппы называются нормальными подгруппами (нормальными делителями). Используется обозначение НG. Условие нормальности, как нетрудно видеть, можно переписать в виде gH = Hg, или gHg^-1 = Н. В абелевой группе все подгруппы являются нормальными.

Если Н – нормальная подгруппа группы G, то множество смежных классов группы G по подгруппе Н можно наделить групповой структурой. Соответствующая группа называется фактор-группой группы G по подгруппе Н и обозначается G/H. Определим композицию смежных классов по формуле (g₁H)(g₂H) =g₁g₂H. Докажем корректность. Пусть g₁h₁ и g₂h₂ —другие представители смежных классов. Toгда g₁h₁g₂h₂ можно представить в виде g₁g₂h´₁h₂ так как в силу gH=Hg произведение h₁g₂ представить в видс g₂h´₁. По­тому (g₁h₁g₂h₂)Н=(g₁g₂)((h´₁h₂)Н)= g₁g₂Н.

Теорема 3.4.1 (о гомоморфизме). Пусть f: G  G₁ — эпиморфизм. Тогда

ker f  G, причем группа G₁ изоморфна фактор-группе G/ker f. Если Н – нормальная подгруппа группы G, то f:GG/H, определяемое условием f(а)=аН, является эпиморфизмом, причем ker f = Н.

3.2.5. Группы подстановок

Обозначим через Х конечное множество, а его элементы – через 1,2,...,п. Рассмотрим все биекции (подстановки) : Х  X. Легко видеть, что они образуют группу относительно операции композиции отображений. Эта группа называется симметрической группой п-й степени и обозначается через S_n или через S(X). Нетрудно показать, что |S_n |= п!. Так, например, группа S₃ состоит из шести подстановок:

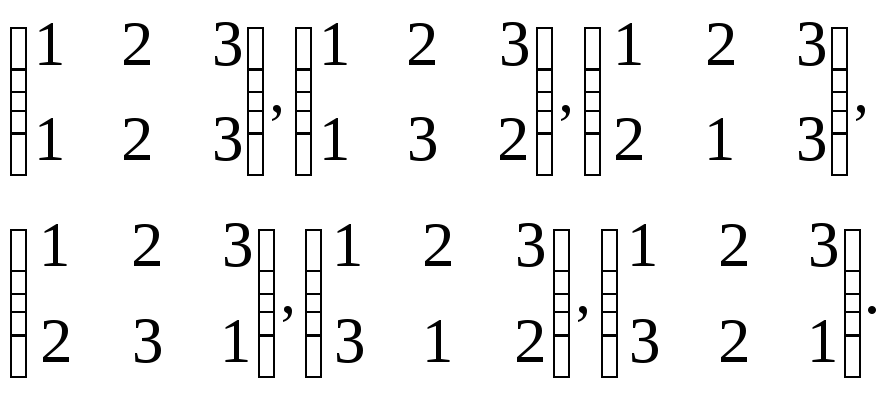
В нижней строке указаны образы элементов 1, 2, 3, расположенных в верхней строке. Условимся при вычислении произведения подстановок ₁₂ выполнять отображения справа налево, т.е. сначала отображение ₂, а затем ₁. Например:

Подгруппы симметрической группы называются группами подстановок.

Подстановку вида 123…k1 назовем циклом длиной k и обозначим (1,2,…,k). Два цикла называются независимыми, если перемещаемые ими элементы попарно различны. Независимые циклы коммутируют, т. e. для них выполнено условие ₁₂ =₂₁. Цикл длиной 2 называется транспозицией.

Теорема 1. Каждая подстановка единственным образом разложима в произведе­ние независимых циклов.

Теорема 2. Каждая подстановка  S_n является произведением транспозиций.

Ни о какой единственности не может быть и речи хотя бы потому, что для любой транспозиции  и подстановки  имеем ²=. Тем не менее, характер четности числа k в разложении подстановки в произведение транспозиций =₁₂…_k определяется подстановкой  однозначно. В самом деле, умножение подстановки на транспозицию меняет характер четности перестановки =a₁a₂…a_n на противоположный. Поэтому, если транспозиции ₁₂…_k приводят перестановку a₁a₂…a_n к виду 1,…,n, то =_k…₁, и наоборот, поэтому характер четности подстановки  совпадает с характером четности перестановки a₁a₂…a_n. Подстановка называется четной или нечетной в зависимости от четности числа k.

Теорема 3. При п > 1 количество четных подстановок равно количест­ву нечетных подстановок и равно п!/2.

Нетрудно показать, что все четные перестановки образуют подгруппу группы S_n. Эта подгруппа называется знакопеременной группой и обозначается через А_n. При n>1 имеем разложение S_n = А_n (1,2)А_n. Поэтому [S_n: А_n]=2. Для любой подстановки S_n смежные классы А_n и А_n состоят из всех четных или всех нечетных подстановок в зависимости от четности подстановки . Поэтому S_n S_n.

Теорема 4 (Кэли). Всякая конечная группа G изоморфна подгруппе симметрической группы S_n, где п =|G |.