
- •Криптографическая защита информации
- •Оглавление
- •Раздел 1. Общие подходы к криптографической защите информации
- •Тема 1. Теоретические основы криптографии
- •1.1. Криптография
- •1.2. Управление секретными ключами
- •1.3. Инфраструктура открытых ключей.
- •1.4. Формальные модели шифров
- •1.5. Модели открытых текстов
- •Тема 2. Простейшие и исторические шифры и их анализ
- •Тема 3. Математические основы криптографии
- •3.1. Элементы алгебры и теории чисел
- •3.1.1. Модулярная арифметика. Основные определения.
- •3.1.2. Алгоритм Евклида нахождения наибольшего общего делителя
- •3.1.3. Взаимно простые числа
- •3.1.4. Наименьшее общее кратное
- •3.1.5. Простые числа
- •3.1.6. Сравнения
- •3.1.7. Классы вычетов
- •3.1.8. Функция Эйлера
- •3.1.9. Сравнения первой степени
- •3.1.10. Система сравнений первой степени
- •3.1.11. Первообразные корни
- •3.1.12. Индексы по модулям рk и 2рk
- •3.1.13. Символ Лежандра
- •3.1.14. Квадратичный закон взаимности
- •3.1.15. Символ Якоби
- •3.1.16. Цепные дроби
- •3.1.17. Подходящие дроби
- •3.1.18. Подходящие дроби в качестве наилучших приближений
- •3.2. Группы
- •3.2.1. Понятие группы
- •3.2.2. Подгруппы групп
- •3.2.3. Циклические группы
- •3.2.4. Гомоморфизмы групп
- •3.2.5. Группы подстановок
- •3.2.6. Действие группы на множестве
- •3.3. Кольца и поля
- •3.3.1. Определения
- •3.3.2. Подкольца
- •3.3.3. Гомоморфизмы колец
- •3.3.4. Евклидовы кольца
- •3.3.5. Простые и максимальные идеалы
- •3.3.6. Конечные расширения полей
- •3.3.7. Поле разложения
- •3.3.8. Конечные поля
- •3.3.9. Порядки неприводимых многочленов
- •3.3.10. Линейные рекуррентные последовательности
- •3.3.11. Последовательности максимального периода
- •3.3.12. Задания
- •Тема 4. Классификация шифров
- •4.1. Классификация шифров по типу преобразования
- •4.2. Классификация шифров замены
- •4.3 Шифры перестановки
- •4.3.1. Маршрутные перестановки
- •4.3.2. Элементы криптоанализа шифров перестановки
- •4.4. Шифры замены
- •4.4.1. Поточные шифры простой замены
- •4.4.2. Криптоанализ поточного шифра простой замены
- •4.4.3. Блочные шифры простой замены
- •4.4.4. Многоалфавитные шифры замены
- •4.4.5. Дисковые многоалфавитные шифры замены
- •4.5. Шифры гаммирования
- •4.5.1. Табличное гаммирование
- •4.5.2. О возможности восстановления вероятностей знаков гаммы
- •4.5.3. Восстановление текстов, зашифрованных неравновероятной гаммой
- •5.5.4. Повторное использование гаммы
- •4.5.5. Криптоанализ шифра Виженера
- •Тема 5. Поточные шифры
- •5.1. Принципы построения поточных шифрсистем
- •Примеры поточных шифрсистем
- •5.3. Линейные регистры сдвига
- •5.4. Алгоритм Берлекемпа-Месси
- •5.5. Усложнение линейных рекуррентных последовательностей
- •5.6. Методы анализа поточных шифров
- •6. Блочные шифры
- •6.1. Принципы построения блочных шифров
- •6.2. Примеры блочных шифров
- •6.3. Режимы использования блочных шифров
- •6.4. Комбинирование алгоритмов блочного шифрования
- •6.5. Методы анализа алгоритмов блочного шифрования
- •6.6. Рекомендации по использованию алгоритмов блочного шифрования
- •7. Криптографические хэш-функции
- •7.1. Функции хэширования и целостность данных
- •7.2. Ключевые функции хэширования
- •7.3. Бесключевые функции хэширования
- •7.4. Целостность данных и аутентификация сообщений
- •7.5. Возможные атаки на функции хэширования
- •Тема 8. Криптосистемы с открытым ключом
- •8.1. Шифрсистема rsa
- •8.2. Шифрсистема Эль-Гамаля
- •8.3. Шифрсистема Мак-Элиса
- •8.4. Шифрсистемы на основе "проблемы рюкзака"
4.5.3. Восстановление текстов, зашифрованных неравновероятной гаммой
Пример (использования шифра модульного гаммирования)
Рассмотрим следующую постановку задачи. Пусть при использовании шифра модульного гаммирования в результате, например, некоторой неисправности гаммообразующего устройства, т.е. устройства, вырабатывающего гамму, в ней встречаются не все знаки. Предположим, далее, что гамма состоит лишь из знаков 1,...,m, т < п, которые встречаются с вероятностями r1,...,rm, соответственно. Будем также предполагать, что исходный открытый текст является обычным литературным текстом. В этих условиях требуется дешифровать полученную криптограмму.
Заметим, что к подобной постановке задачи можно было прийти иначе. Выделив несколько знаков гаммы, имеющих достаточную суммарную вероятность, например 0.8, предположим, что лишь они использовались при шифровании. Это предположение может привести к потере истинного варианта при построении некоторого метода вскрытия. Вероятность потери можно оценить при этом стандартными методами статистики.
При решении поставленной задачи примем во внимание, что в i-м такте шифрованию подлежала одна из следующих букв открытого текста:
ti(1)=si – 1,..., ti(m)=si – m, (8)
где si – буква шифртекста.
Поэтому знаки открытого текста следует искать в колонках таблицы, изображенной на рис. 9:
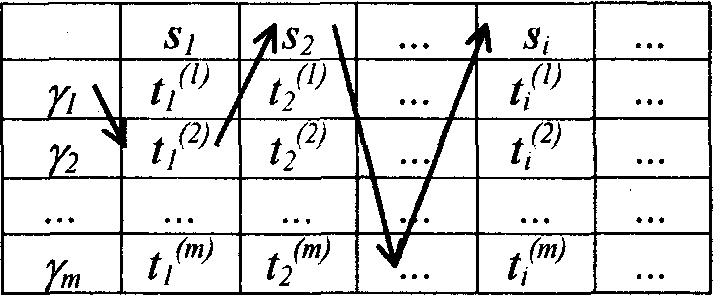
Рис.9
Отбирая по одному знаку из каждой колонки так, чтобы получился "читаемый" текст, мы получим возможность восстановить открытый текст.
Описанный метод относится к классу так называемых методов бесключевого чтения (когда открытый текст восстанавливается без предварительного определения ключа) и называется методом чтения в колонках.
Метод чтения в колонках можно усовершенствовать за счет упорядочения букв в колонках. В самом деле, в каждом такте возможные знаки открытого текста t(1)=s – 1,..., t(m)=s – m имеют априорные вероятности рt(1),...,рt(m), которые считаются известными. В нашем случае имеется также дополнительная информация, а именно, известно, что произошло событие "si = s". При этом
p{si=s/ ti=t(k)}= rk , k=1,…,m.
О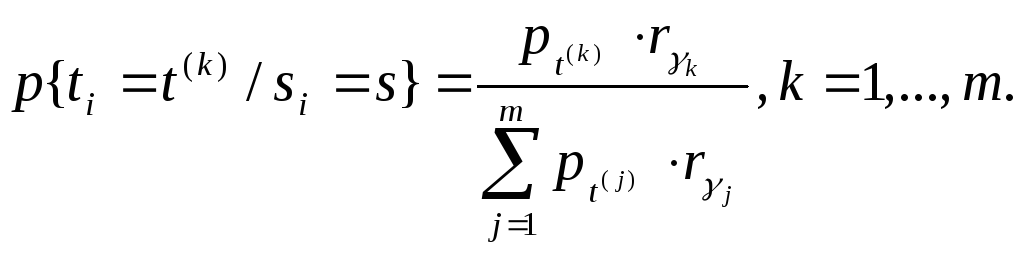 тсюда
по формуле Байеса получаем
тсюда
по формуле Байеса получаем
(9)
Теперь можно упорядочить вероятности (8) знаков открытого текста в каждой колонке таблицы в соответствии с убыванием вычисленных апостериорных вероятностей. Поступив таким образом, мы поместим наиболее вероятные знаки открытого текста в начало таблицы, чем облегчим чтение в колонках.
С ростом т чтение в колонках становится затруднительным, а при т=п и при условии, что при шифровании использовалась случайная равновероятная гамма, каждая колонка содержит все знаки алфавита, ни одному из которых нельзя отдать предпочтения. Поэтому в последовательности колонок можно прочитать любой текст, то-есть нет возможности получить информацию об истинном сообщении.
Пример (использования неисправности в реализации шифра Вернама)
Рассмотрим шифр гаммирования, определяемый уравнением (4), называемый шифром Вернама. Знаки открытого текста и знаки гаммы представляются при этом 5-мерными двоичными векторами.
В случае обрыва одного из "проводков", идущих от источника гаммы, последовательность знаков гаммы будет содержать лишь половину возможных своих значений. Соответствующая координата в любом 5-мерном векторе гаммы будет равна нулю. В случае обрыва двух или большего числа "проводков" векторы гаммы будут содержать два или большее число нулевых координат. Число возможных знаков гаммы будет сокращаться вдвое при каждом обрыве. Таким образом, подобная неисправность схемы приводит к постановке задачи, указанной в предыдущем пункте. В рассматриваемом случае подобную неисправность можно обнаружить по шифртексту.
Покажем, как это сделать при условии, что "исправная" гамма является случайной и равновероятной. Будем при этом рассматривать позначные модели открытого текста, гаммы и шифртекста, то есть считать, что они являются реализациями случайных независимых испытаний полиномиальных схем с соответствующими распределениями вероятностей р(А), r(A), s(A) на знаках открытого текста, гаммы и шифртекста. Естественно также условиться, что распределения р(А) и r(А) являются независимыми. При этом распределение s(A) определяется формулой
(![]() 10)
10)
где х – знак открытого текста, – знак гаммы, у – знак шифртекста.
Итак, в нашем случае алфавитом открытого текста, шифрованного текста и гаммы является множество
А={(а1,а2,а3,а4,а5) : аi Z2 , i=1,…,5},
образующее абелеву группу относительно операции покоординатного сложения векторов по модулю 2. При обрыве, например, первого соединения возможные знаки гаммы образуют подмножество
В={(0, 2, 3, 4, 5) : i Z2 , i=2,…,5},
являющееся подгруппой группы (А, ). Точно так же и при любых других обрывах множество знаков гаммы образует подгруппу В группы (А, ).
Разложим группу А = {а1,…,аn} в левые смежные классы по подгруппе В :
А=В (g2B) …(grB), (11)
где gi A, i=2,…,r, – представители соответствующих смежных классов.
Т![]() еперь
с использованием частотных свойств
используемого кода (например, МТК-2 или
др.), аналогичных частотам букв в открытом
текcте,
можно подсчитать значения вероятностей
знаков смежных классов giB,
i=1,…,r,
из разложения (11) по формуле
еперь
с использованием частотных свойств
используемого кода (например, МТК-2 или
др.), аналогичных частотам букв в открытом
текcте,
можно подсчитать значения вероятностей
знаков смежных классов giB,
i=1,…,r,
из разложения (11) по формуле
где a giB. Этот подсчет может быть проведен для любых комбинаций обрывов. Теперь остается определить частоты символов шифртекста и сравнить их с рассчитанными заранее эталонными диаграммами. Сравнение выявит характер неисправности, и задача восстановления открытого текста будет сведена к чтению в колонках.
Заметим, что вместо 5-мерных можно было рассматривать и n-мерные векторы, п > 5. Предложенный метод работает и в этом, более общем случае.
