3.1.14. Квадратичный закон взаимности

Гаусс доказал следующую лемму, упрощающую вычисление символа Лежандра.

Лемма 1. где

Теорема 1 (квадратичный закон взаимности). Для любых нечетных простых р, q выполнено равенство

3.1.15. Символ Якоби

Символ Якоби является обобщением символа Лежандра и служит для упрощения вычисления последнего. Пусть Р – нечетное натуральное число, Р=р₁р₂р_s – его разложение на простые множители. Для всякого целого а, (a,Р)=1, символ Якоби определяется по формуле

Отметим следующие свойства.

Свойство 1.

Свойство 2.

Свойство 3.

Свойство 4.

Заметим, что из равенства нe следует, что а является квадратичным

вычетом по модулю Р. В действительности, а является квадратичным вычетом по модулю Р тогда и только тогда, когда а — квадратичный вычет по модулю

каждого простого р_i, i= 1, 2, ..., s. В то же время из равенства следует, что a – квадратичный невычет по mod P.

Теорема 1. Пусть Р и Q – положительные взаимно простые нечет­ные модули. Тогда

3.1.16. Цепные дроби

Пусть  – положительное вещественное число. Положим q₁ =[]. Тогда, если  нецелое, то

где ₂ >1. Продолжая этот процесс, получаем

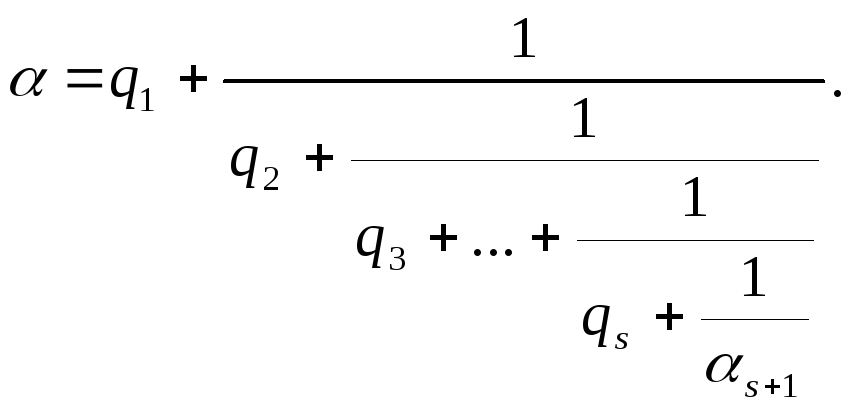Следовательно

Представление  в указанном виде называется разложением  в цепную (не­прерывную) дробь. При иррациональном  цепная дробь, очевидно, оказывает­ся бесконечной. При рациональном  дробь будет конечной. Покажем это.

Пусть  =a/b . Применим алгоритм Евклида:

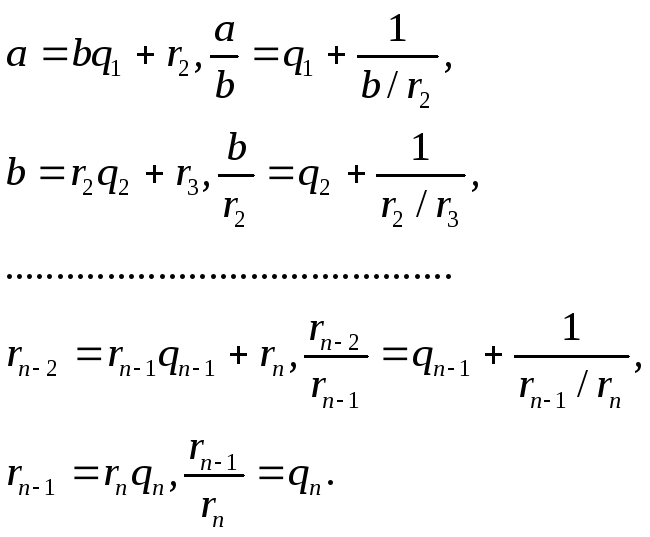
Следовательно,

Теорема 1. Всякое иррациональное  разлагается в бесконечную цепную дробь. Всякое рациональное  разлагается в конечную цепную дробь.

3.1.17. Подходящие дроби

Далее будем использовать запись

 =[ q₁, q₂,…, q_s, _s+1].

Числа q₁, q₂,…, q_s называются неполными частными, а рациональное число _s= [q₁, q₂,…, q_s] – s-й подходящей дробью числа  . Через Р_s обозначается числитель, а через Q_s – знаменатель подходящей дроби _s.

Например, P₁ =q₁, Q₁ =1. Удобно считать, что Р₀ =1, Q₀ =0. Имеет место следующий закон образования подходящих дробей.

Теорема 1. Р_s =q_sP_s-1 +P_s-2 , Q_s =q_sQ_s-1 +Q_s-2

Теорема 2. _s –_s-1 =(–1)^s/(Q_sQ_s-1). Р_sQ_s-1 – Q_sP_s-1 =(–1)^s

Следствие 1. Все подходящие дроби несократимы.

Теорема 3. При _s  подходящие дроби ₁,₂,..., _s, с четными номерами являются последовательными приближениями , с одной стороны, а с нечетными номерами – с другой, т.е.

₁ <  ₃< ...<  < ...< ₄ <₂.

3.1.18. Подходящие дроби в качестве наилучших приближений

Несократимую дробь a/b(b > 0) назовем наилучшим приближением первого рода числа   R, если

В случае, когда выполняется условие

говорят о наилучшем приближении второго рода, которое является и наилучшим приближением первого рода. Обратное утверждение неверно. Легко проверить, что 1/3 является наилучшим приближением лишь первого рода числа 1/5.

Теорема 1. Всякая подходящая дробь _s, s>1 есть наилучшее при­ближение второго рода.

Теорема 2. |Q_s-1– P_s-1| > |Q_s – P_s |, а значит, | – P_s-1/Q_s-1| > |  – P_s/Q_s|.

Теорема 3. Если P/Q – несократимая дробь, Q > 0, такая, что

то P/Q – подходящая дробь числа  .

В заключение отметим факт, который потребуется в дальнейшем:

При разложении рационального числа P/Q в цепную дробь длина последней ограничена сверху величиной 2log₂Q +1.

Задания

1. Показать, что 30 | т⁵ – т, 6|т(т² + 5), 42 | т⁷ – т, 30 | тп(т⁴ – n⁴) при лю­бых натуральных т, п.

2. Показать, что при натуральном т произведение (т + 1)(m + 2) ••• (т + т) делится на 2^m.

3. Будут ли целыми числа

4. Пусть (а, b) = 1. Показать, что (a + b, а – b)  2.

5. Вычислить НОДы: (549, 387), (589, 343), (12606, 6494), (6188, 4709) и найти их линейные разложения.

6. Доказать, что НОД можно определить как такой общий делитель, который делится на любой другой общий делитель.

7. Пусть (а,b) = 1, ab = с² . Показать, что числа а и b будут квадратами.

8. Показать, что р² – q² кратно 24, где р, q – простые числа, большие 3.

9. Доказать бесконечность множества простых чисел вида 4т + 3.

10. Доказать бесконечность множества простых чисел вида 6m+ 5.

11. Пусть k – натуральное. Доказать, что в натуральном ряду имеется бесконечно много отрезков т, т + 1,..., т + k, не содержащих простых чисел.

12. Найти канонические разложения чисел 82798848, 81057226635.

13. Разложить на простые множители числа 10!, 15!, 20!, 30!.

14. Сколькими нулями оканчиваются числа 50!, 100!?

15. Найти функцию Эйлера для чисел 375, 720, 957, 988, 1200, 4320.

16. Сколько чисел в интервале от 1 до 120 не взаимно простых с 30?

17. Дано (а) =120, а = рq, где р, q – простые. Найти a, если р – q =2.

18. Доказать, что уравнение 15х² – 7у² = 9 не имеет решений в целых числах.

19. Решить в целых числах уравнение х² + у² = z².

20. Доказать, что сумма квадратов пяти последовательных целых чисел не мо­жет быть точным квадратом.

21. Решить в целых числах уравнения 53х + 47у =1, 22х + 32у =18.

22. Путем перебора решить сравнения:

1) 5х² – 15х +220(mod 3), 4) 7x  31(mod 6),

2) х³ – 12 0(mod 5), 5) 12x  1(mod 7),

3) 3х  1(mod 5), 6) 6x + 5  6(mod 7).

23. Способом Эйлера решить сравнения:

1) 5х  0(mod 7), 3) 5x  7(mod 7),

2) 25х  15(mod 7), 4) 5x  26(mod 12).

24. Решить системы сравнений:

x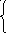  3(mod 8), x  2(mod l7),

х  11(mod 20), 5x  3(mod 9),

x  l(mod l5), 8x  4(mod l4).

25. Решить системы сравнений китайским способом:

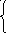x  2(mod 7), x  3(mod 8),

x  9(mod 11), x  2(mod 9),

x  3(mod 13), x  5(mod 7).

26. Составить таблицы индексов:

1. по mod 29 с основанием 2,

2. по mod 23 с основанием 5.

Путем индексирования решить сравнения:

1) 2^х  (mod 67), 5) 37х¹⁶  62(mod 73),

2) 52^х 38(mod 29), 6) 2x³  17(mod 41),

3) 13^х  (mod 47), 7) 5x⁴  3(mod 11).

4) 12^х  17(mod 31), 8) 27x⁵  2(mod 31).

27. Пусть а принадлежит показателю , b – показателю , (,)=1. Показать, что ab принадлежит показателю .

28. Пусть а принадлежит показателю , b – показателю . Как построить элемент, принадлежащий показателю [,]?

29. Пусть а принадлежит показателю . Какому показателю принадлежит a^?

30. Пусть g – первообразный корень по модулю т. Сколько всего первообраз­ных корней по этому модулю?

31. Вычислить символы Лежандра и Якоби:

32. Найти все квадратичные вычеты по модулю числа р:

р=11, p=13, р=17.

33. Доказать, что при р = 4k + 1 числа а и р-а — одновременно квадратичные вычеты или невычеты, а при р= 4k + 3 — наоборот.

34. Решить сравнения: х² 19 (mod 31), х²  15 (mod 53), x² 11 (mod 59).

35. Решить сравнения: х² + 8х – 20  0(mod 45), 5x² + х + 4  0(mod 10).

36. Пользуясь леммой Гаусса и представлением

доказать, что

37. Показать, что для любого целого d и любого нечетного простого р количество решений сравнения х²  d (mod p) равно

38. Найти способ решения сравнений вида х²  4(mod m).

39. Доказать, что количество решений уравнения х² + у² = р, (х,у)=1, х >0, у>0 равно количеству решений сравнения z² + 1  0(mod p).

40. Разложить в цепные дроби числи 170/109, 99/170, 125/92, .