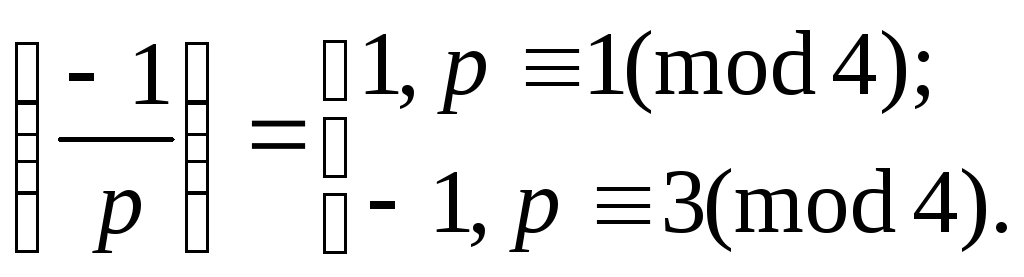- •Криптографическая защита информации
- •Оглавление
- •Раздел 1. Общие подходы к криптографической защите информации
- •Тема 1. Теоретические основы криптографии
- •1.1. Криптография
- •1.2. Управление секретными ключами
- •1.3. Инфраструктура открытых ключей.
- •1.4. Формальные модели шифров
- •1.5. Модели открытых текстов
- •Тема 2. Простейшие и исторические шифры и их анализ
- •Тема 3. Математические основы криптографии
- •3.1. Элементы алгебры и теории чисел
- •3.1.1. Модулярная арифметика. Основные определения.
- •3.1.2. Алгоритм Евклида нахождения наибольшего общего делителя
- •3.1.3. Взаимно простые числа
- •3.1.4. Наименьшее общее кратное
- •3.1.5. Простые числа
- •3.1.6. Сравнения
- •3.1.7. Классы вычетов
- •3.1.8. Функция Эйлера
- •3.1.9. Сравнения первой степени
- •3.1.10. Система сравнений первой степени
- •3.1.11. Первообразные корни
- •3.1.12. Индексы по модулям рk и 2рk
- •3.1.13. Символ Лежандра
- •3.1.14. Квадратичный закон взаимности
- •3.1.15. Символ Якоби
- •3.1.16. Цепные дроби
- •3.1.17. Подходящие дроби
- •3.1.18. Подходящие дроби в качестве наилучших приближений
- •3.2. Группы
- •3.2.1. Понятие группы
- •3.2.2. Подгруппы групп
- •3.2.3. Циклические группы
- •3.2.4. Гомоморфизмы групп
- •3.2.5. Группы подстановок
- •3.2.6. Действие группы на множестве
- •3.3. Кольца и поля
- •3.3.1. Определения
- •3.3.2. Подкольца
- •3.3.3. Гомоморфизмы колец
- •3.3.4. Евклидовы кольца
- •3.3.5. Простые и максимальные идеалы
- •3.3.6. Конечные расширения полей
- •3.3.7. Поле разложения
- •3.3.8. Конечные поля
- •3.3.9. Порядки неприводимых многочленов
- •3.3.10. Линейные рекуррентные последовательности
- •3.3.11. Последовательности максимального периода
- •3.3.12. Задания
- •Тема 4. Классификация шифров
- •4.1. Классификация шифров по типу преобразования
- •4.2. Классификация шифров замены
- •4.3 Шифры перестановки
- •4.3.1. Маршрутные перестановки
- •4.3.2. Элементы криптоанализа шифров перестановки
- •4.4. Шифры замены
- •4.4.1. Поточные шифры простой замены
- •4.4.2. Криптоанализ поточного шифра простой замены
- •4.4.3. Блочные шифры простой замены
- •4.4.4. Многоалфавитные шифры замены
- •4.4.5. Дисковые многоалфавитные шифры замены
- •4.5. Шифры гаммирования
- •4.5.1. Табличное гаммирование
- •4.5.2. О возможности восстановления вероятностей знаков гаммы
- •4.5.3. Восстановление текстов, зашифрованных неравновероятной гаммой
- •5.5.4. Повторное использование гаммы
- •4.5.5. Криптоанализ шифра Виженера
- •Тема 5. Поточные шифры
- •5.1. Принципы построения поточных шифрсистем
- •Примеры поточных шифрсистем
- •5.3. Линейные регистры сдвига
- •5.4. Алгоритм Берлекемпа-Месси
- •5.5. Усложнение линейных рекуррентных последовательностей
- •5.6. Методы анализа поточных шифров
- •6. Блочные шифры
- •6.1. Принципы построения блочных шифров
- •6.2. Примеры блочных шифров
- •6.3. Режимы использования блочных шифров
- •6.4. Комбинирование алгоритмов блочного шифрования
- •6.5. Методы анализа алгоритмов блочного шифрования
- •6.6. Рекомендации по использованию алгоритмов блочного шифрования
- •7. Криптографические хэш-функции
- •7.1. Функции хэширования и целостность данных
- •7.2. Ключевые функции хэширования
- •7.3. Бесключевые функции хэширования
- •7.4. Целостность данных и аутентификация сообщений
- •7.5. Возможные атаки на функции хэширования
- •Тема 8. Криптосистемы с открытым ключом
- •8.1. Шифрсистема rsa
- •8.2. Шифрсистема Эль-Гамаля
- •8.3. Шифрсистема Мак-Элиса
- •8.4. Шифрсистемы на основе "проблемы рюкзака"
3.1.11. Первообразные корни
Говорят, что число а, взаимно простое с модулем т, принадлежит показателю , если — такое наименьшее натуральное число, что выполняется сравнение a l(mod т). Справедливы следующие свойства.
Свойство 1. Числа a0, a1,…, a -1 попарно несравнимы по модулю т.
Свойство 2. а a (mod т) <=> (mod ).
Свойство 3. |(т). Число, принадлежащее показателю (т), называется первообразным корнем по модулю т.
Свойство 4. По любому простому модулю р существует первообразный корень.
Гауссом доказано существование первообразных корней по модулям рk и 2рk при любом нечетном простом р. Легко убедиться, что при т = 4 первообразный корень также существует. Таким образом, первообразные корни существуют по модулям 2, 4, рk, 2 рk, где р — нечетное простое, kN.
Первообразные корни по всем остальным модулям отсутствуют.
Нахождение первообразных корней упрощает следующее свойство.
Свойство 5. Пусть с = (т) и q1,q2, ...,qk — различные простые делители числа с. Число a, взаимно простое с модулем т, будет первообразным корнем тогда и только тогда, когда не выполнено ни одно из следующих сравнений:
ac/q1 1(mod m), ac/q2 l(mod m),..., ac/qk l(mod m). (3.1.11.1)
Пример. Пусть т = 41. Имеем с =(41) = 40= 23•5. Итак, первообразный корень не должен удовлетворять двум сравнениям
а8 1(mod 41), a20 l(mod 41).
Испытываем числа 2, 3, 4, ...: 28 10, 220 1, 38 1, 48 18, 420 1, 58 18, 520 1, 68 = 10, 620 = 40. Отсюда видим, что 6 является наименьшим первообразным корнем по модулю 41.
3.1.12. Индексы по модулям рk и 2рk
Обозначим через т модуль вида рk или 2рk, а через g – первообразный корень по этому модулю. Положим с=(т).
Свойство 1. Если число принимает последовательно значения 0, 1, ..., с -1, то g пробегает приведенную систему вычетов по модулю т.
Для чисел а, взаимно простых с т, введем понятие индекса, называемого иногда дискретным логарифмом.
Пусть а g(mod т). Число ( 0) называется индексом числа а по модулю т при основании g. Используются обозначения = indga или = ind а. В силу теоремы Эйлера индекс определен по модулю с. Тем самым было бы правильнее говорить о классе вычетов по модулю с.
Свойство 2. ind ab ind а + ind b (mod с).
Свойство 3. ind an n ind а(modc).
Если воспользоваться таблицами индексов, то можно решать показательные и степенные сравнения путем их индексирования (дискретного логарифмирования). В самом деле, степенное сравнение xn a(mod т) равносильно сравнению n ind x ind a(modc), решение которого при наличии таблиц не составляет труда. Положим d = (п, с).
Свойство 4. Сравнение хn a(mod т) разрешимо тогда и только тогда, когда d делит ind а. В случае разрешимости имеется d решений.
3.1.13. Символ Лежандра
В п. 3.1.9 мы изучали сравнение ax b(modm). Рассмотрим сравнение ax2+bх+ с 0 (mod m). Путем выделения квадрата приведем его к виду (2ах + b)2 = b2 – 4ас (mod 4am). Полагая у = 2ax + b, d = b2 – 4ас, имеем сравнение у2d(mod4am). Фактически исходное сравнение сведено к сравнению вида х2а(mod m). Рассмотрим случай, когда т – простое.
П![]()
![]()
![]()
![]() усть
р – нечетное
простое число, (а,р)=1.
Символ
Лежандра определяется
равенством =1, если сравнение х2
a(mod
р)
разрешимо, и = –1
в противном случае. Говорят также, что
в первом случае а
является квадратичным
вычетом по
модулю р
и квадратичным
невычетом
во втором.
усть
р – нечетное
простое число, (а,р)=1.
Символ
Лежандра определяется
равенством =1, если сравнение х2
a(mod
р)
разрешимо, и = –1
в противном случае. Говорят также, что
в первом случае а
является квадратичным
вычетом по
модулю р
и квадратичным
невычетом
во втором.
Таким образом, = 1.
П![]()
![]()
![]() ример.
Квадратичные вычеты по mod 7 –
это 1, 2, 4: невычеты –
3, 5, 6. Если g
–
первообразный корень по mod
p, то каждое
целое g2k
–
квадратичный вычет, а каждое g2k+1
– квадратичный
невычет.
ример.
Квадратичные вычеты по mod 7 –
это 1, 2, 4: невычеты –
3, 5, 6. Если g
–
первообразный корень по mod
p, то каждое
целое g2k
–
квадратичный вычет, а каждое g2k+1
– квадратичный
невычет.
Свойство 1. = , где (а,р)=(b,р) =1.
Теорема 1 (критерии Эйлера). Если (а,р)=1, то
![]()
Свойство
2.