5.5. Усложнение линейных рекуррентных последовательностей

Алгоритм Берлекемпа-Месси позволяет для каждой линейной рекуррентной последовательности построить вырабатывающий ее линейный регистр сдвига минимальной длины. Однако при создании стойких криптографических алгоритмов необходимо гарантировать определенную величину линейной сложности не для одной конкретной ЛРП, а для целого класса псевдослучайныx последовательностей, получаемых при различныx ключах. При этом, как правило, мощность класса рассматриваемых последовательностей бывает настолько велика, что применить алгоритм Берлекемпа-Месси к каждой последовательности не представляется возможным. Поэтому важной криптографической задачей является построение целых классов псевдослучайных последовательностей с высокой линейной сложностью.

Описанные выше свойства линейных регистров сдвига показывают, что, несмотря на достаточно большой период и хорошие статистические качества, линейные рекуррентные последовательности имеют очень простое строение. Поэтому в криптографических приложениях используют различные способы усложнения аналитического строения линейных рекуррент.

Фильтрующие генераторы

Первый способ заключается в применении к элементам линейной рекуррентной последовательности некоторой функции f (F(x) –характеристический многочлен, определяющий закон рекурсии ЛРС).

В литературе подобные узлы усложнения ЛРП получит название фильтрующих генераторов. Их результирующей последовательностью является нелинейно "фильтрованное" содержимое регистра сдвига. "Фильтрующая" функция f должна выбираться так, чтобы выходная последовательность имела распределение, близкое к равномерному распределению, и высокую линейную сложность.

Известно, что любая функция над конечным полем может быть задана некоторым полиномом. Поэтому при изучении фильтрующих генераторов достаточно рассмотреть только полиномиальные усложнения линейных рекуррент.

Пусть и – линейная рекуррентная последовательность над полем Р из q элементов с характеристическим многочленом F{x) степени т, и функция f(x₁,...,x_m) имеет вид:

Тогда выходная последовательность фильтрующего генератора определяется следующим равенством:

Рассмотрим случай, наиболее интересный с практической стороны, когда F(x) – примитивный многочлен степени т над полем Р. Поскольку, усложненная последовательность является суммой произведений некоторых линейных рекуррентных последовательностей, отличающихся друг от друга сдвигами, продемонстрируем методику изучения таких последовательностей на примере доказанной А.А.Нечаевым теоремы о произведении линейной рекуррентной последовательности на ее сдвиг.

Теорема 3. Пусть и – линейная рекуррентная последовательность над полем Р = GF(q) характеристики р с примитивным характеристическим многочленом F(x) cmeпени т, элементы которой задаются равенством

где  – корень F(x) в поле GF(q^т) из q^т элементов, аGF(q^т). Тогда элементы последователь­ности v, задаваемой равенством

v(i)= u{i) • u(i + k), i>0,

удовлетворяют соотношению

где если т=2, s=;

в остальных случаях.

Следствие. Если в условиях теоремы 0 <k < m, m >7, то

где М_S(x) – минимальный многочлен элемента над полем GF(q).

В общем случае описание строения минимального многочлена линейной рекуррентной последовательности удобно проводить, исходя из свойств его корней.

Для примитивного многочлена F(x) с корнем  обозначим через F^(t)(x) многочлен вида

где W_q(k) обозначает q-ичный вес числа k, то есть число ненулевых цифр в q-ичной записи числа k. Положим

Утверждение 4. Пусть и – линейная рекуррентная последовательность над полем GF(q) c примитивным характеристическим многочленом F(x) степени т,  – корень F(x) в GF(q^т). Тогда ранг последовательности v, полученной из последовательности и помощью функции f(x₁,...,x_m), degf(x)<r, не превосходит degF^<t>(x), причем многочлен F^<t>(x) является характеристическим многочленом последовательности v.

Таким образом, несмотря на то, что фильтрованную последовательность нельзя получить с помощью сдвигового регистра с линейной обратной связью той же длины, что и исходный регистр, ее всегда можно получить с помощью регистра большей длины.

Заметим, что степень многочлена F^(t)(x) равна числу целочисленных

наборов (i₀,...,i_{m –1}), таких, что 0<i_j<q, и представляется в виде

Данная величина является верхней оценкой линейной сложности класса выходных последовательностей фильтрующего генератоpa, полученных при различных начальных заполнения регистра сдвига. Задача получения нижних оценок ранга усложнений линейных рекуррент представляется существенно более сложной. В частности, даже если ограничиться классом последовательностей, полученных с помощью функций усложнения фиксированной степени нелинейности, то в этом классе будут содержаться рекурренты, линейная сложность которых меняется в диапазоне от т degF^<t>(х).

Таким образом, для получения псевдослучайных последовательностей с высоким уровнем линейной сложности функция усложнения фильтрующего генератора должна иметь достаточно высокую степень нелинейности.

Комбинирующие генераторы

Второе направление синтеза псевдослучайных последовательностей с высокой линейной сложностью связано с использованием в одной схеме нескольких линейных peгистров сдвига. Генератор псевдослучайных последовательностей, реализующий усложнение нескольких линейных рекуррент с помощью одной общей функции усложнения, получил название комбинирующего генератора.

Рассмотрим один частный случай комбинирующего генератора, когда функция усложнения f имеет степень нелинейности t, и ее представление свободно от квадратов:

(5.7)

Теорема 4. Пусть и₁,...,и_t —ЛРП максимального периода с примитивными характеристическими многочленами F₁(х),...,F_t(х) над полем GF(q) попарно взаимно простых степеней: n_s= degF_s(x), (n_s, n_j)=1 для s j, s,j=1,…,t.

Тогда для функции усложнения вида (7) линейная сложность последовательности v вида v(i)=f(u₁(i),u₂(i),…,u_t(i)), i 0

равна (5.8)

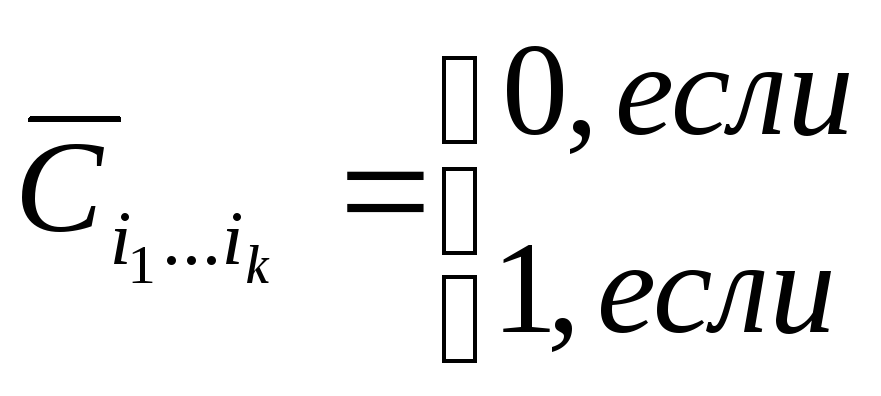
где

Композиции линейных регистров сдвига

Рассмотрим еще один тип генераторов, представляющий собой композицию линейных регистров сдвига. Так называется схема, в которой выход одного из регистров подается на вход другого регистра.

Функционирование такой схемы описывается следующим образом. Пусть v – ЛРП, вырабатываемая первым регистром сдвига, закон рекурсии которого определяется характеристическим многочленом F(x).

Пусть задано начальное состояние второго регистра сдвига, закон рекурсии которого определяется характеристическим многочленом

Тогда выходная последовательность композиции регистров сдвига задается соотношением

Непосредственно из определения композиции регистров сдвига вытекает, что минимальный многочлен выходной последовательности делится на минимальный многочлен последовательности v и делит произведение F(x)G(x).

Схемы с динамическим изменением закона рекурсии

Рассмотренные способы усложнения линейных рекуррент объединяет идея повышения линейной сложности исходных последовательностей за счет применения дополнительных функций усложнения. При этом законы функционирования регистров остаются неизменными.

Альтернативный способ усложнения ЛРП состоит в изменении закона рекурсии в процессе работы криптографического алгоритма. Привлекательным представляется использование нелинейной логики в цепи обратной связи регистровых преобразований. Однако общая теория подобных схем еще недостаточно разработана, в связи с чем трудно гарантировать необходимые свойства соответствующих последовательностей.

Один из путей построения подобных схем основан на динамическом изменении закона рекурсии линейного регистра сдвига.

Рассмотрим, например, вопрос о строении псевдослучайной последовательности, получаемой с помощью линейного регистра сдвига, закон функционирования которою меняется в зависимости от четности номера вырабатываемого знака.

Рассмотрим два многочлена А(х)=х^т + а_jх^j, В(х) =х^т +  b_k х^k степени т и последовательность v, удовлетворяющую условиям:

Ясно, что в четных тактах закон рекурсии последовательности v определяется характеристическим многочленом А(х), а в нечетных тактах – характеристическим многочленом В(х).

Образуем многочлены A⁽⁰⁾(x), A⁽¹⁾(x), B⁽⁰⁾(x), B⁽¹⁾(x) следующим образом:

Несложно проверить, что получаемая в результате последовательность v является линейной рекуррентной последовательностью с характеристическим многочленом

Н(x)=A⁽¹⁾(x)B⁽¹⁾(х) – A⁽⁰⁾(x)B⁽⁰⁾(x).

К классу операторов с динамическим изменением закона рекурсии относятся также линейные регистры сдвига с неравномерным движением информации. Так называются регистры, для которых число тактов работы до получения (i+1)-го знака выходной последовательности зависит либо от значения числа i, либо от состояния регистра в такте i. Получаемая в результате последовательность будет некоторой выборкой с переменным шагом из исходной ЛРП, вырабатываемой линейным регистром сдвига.

В одном из возможных вариантов значение шага выборки меняется в соответствии с некоторой последовательностью периода t. В этом случае удается описать минимальные многочлены получаемых псевдослучайных последовательностей

Теорема 5. Пусть d₀,...,d_{t –1} – набор из t > 1 чисел множества 0,…,qⁿ – 2 и

Пусть при i= kt + r элементы последовательности v задаются

формулой

где с – нулевой, а  — примитивный элементы поля GF(qⁿ). Пусть, кроме того, простые делители числа t делят , но не делят (qⁿ –1,D).

Пусть, наконец, qⁿ  1(тоd 4), если t кратно четырем. Тогда минимальный многочлен М_v(х) последовательности v имеет вид М_v(х)=Р(х^t), где Р(х) –минимальный многочлен элемента  ^D.

Схемы с элементами памяти

Дополнительные возможности для усложнения ЛРП открывает использование в криптографических алгоритмах элементов памяти.

Один из наиболее широко известных классов датчиков псевдослучайных чисел, построенных с использованием памяти, составляют генераторы Макларена-Марсальи. Принцип работы таких генераторов в самом общем виде можно сформулировать следующим образом.

Пусть имеются три последовательности и массив памяти. Будем записывать элементы первой последовательности в память по адресам, которые определяются элементами второй последовательности. Элементы выходной последовательности получаются при считывании значений, хранящихся в массиве памяти, в соответствии с элементами третьей последовательности. Таким образом, первая последовательность определяет, какие знаки заносятся в память, вторая последовательность управляет процессом записи этих элементов в память, а третья – процессом считывания из памяти элементов выходной последовательности.

Рассмотрим частный случай, когда процессами записи и считывания управляет одна и та же последовательность.

Пусть и и v – последовательности над полем Р, а вы­ходная последовательность у вырабатывается с использова­нием q ячеек памяти R₀,...,R_q–1. Если R_j(i) – заполнение j-й ячейки памяти перед началом i-го такта работы схемы, то преобразование информации в i-м такте описывается фор­мулами

y(i)=R_v(i)(i),

если j  v(i),

если j = v(i).

Таким образом, последовательность v определяет адреса, по которым в память записываются элементы последовательности и.

Рассмотрим вопрос о периодах выходных последовательностей генератора Макларена-Марсальи указанного типа.

Пусть последовательность и имеет период , а адресная последовательность v принимает значения 0,1,...,q-1 и имеет период t. Начальное заполнение памяти R₀(0),...,R_q–1(0) выбирается произвольно.

Пусть i₀ – такое наименьшее натуральное число, что для любого k{0,1,..., q–1} существует i {0,1,..., i₀} такое, что v(i)=k. Другими словами, через i₀ тактов работы схемы память будет заполнена только элементами последовательности и.

Теорема 6. Пусть  – период последовательности и, t – период последовательности v, причем (,t)=1,  >t. Тогда для значения периода Т выходной последовательности у выполняется равенство Т=s, где s=t/d и d е^q/e.