3.3.10. Линейные рекуррентные последовательности

Последовательность элементов s₀, s₁,… поля F_q, удовлетворяющих условию

s_n+k = a_k-1s_n+k-1 + a_k-2s_n+k-2 + …+ a₀s_k , (3.3.1)

где a_k-1,a_k-2,…a₀ – фиксированные элементы поля, называется линейной рекуррентой (ЛРП) k-го порядка над полем F_q. Эта последовательность полностью определяется вектором начального состояния S₀= (s₀,s₁,…,s_k-1) и коэффициентами a_k-1,a_k-2,…a₀.

С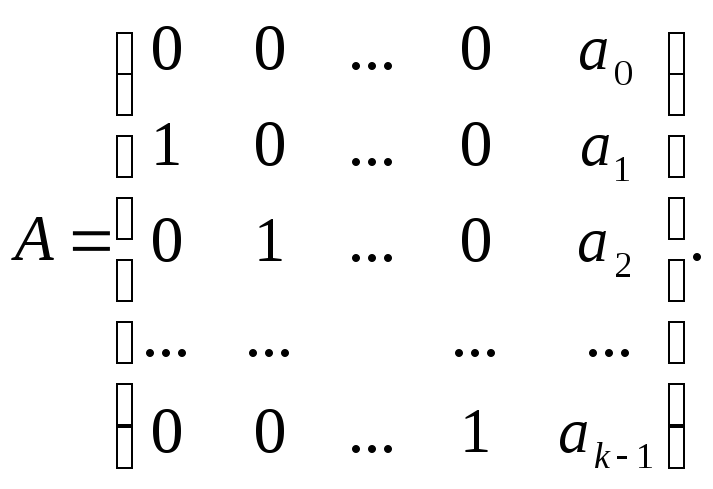 линейной рекуррентой можно связать матрицу

Рассмотрим теперь последующие состояния ЛРП S₁=(s₁, s₂,…,s_k), S₂=(s₂,s₃,…,s_k+1),… Определение (3.3.1) можно переписать в виде

S_i= S_i-1A, i=l, 2,… (3.3.2)

Далее рассматриваются лишь ЛРП с условием a₀0. В этом случае матрица А является элементом группы GL(k,F_q) всех невырожденных матриц k-го по­рядка с элементами из поля F_q. Поскольку эта группа конечна, то матрица А имеет конечный порядок как элемент группы.

Теорема 1. Любая линейная рекуррента при a₀0 является чисто пе­риодической последовательностью.

3.3.11. Последовательности максимального периода

Под периодом ЛРП будем понимать ее минимальный период.

Рассмотрим характеристический многочлен f(x) =|хЕ – S| матрицы S. Легко подсчитать, что f(x)=x^k – s_k-1x^k-1 –...– s₁x– s₀. Можно показать, что он будет такжс и минимальным многочленом матрицы S. Этот многочлен называется характеристическим многочленом ЛРП (3.3.1).

Теорема 1. Пусть многочлен f(x)= |xE-A| неприводим. Тогда его порядок совпадает с порядком матрицы S как элемента группы GL(k, F_q).

Теорема 2. Минимальный период линейной рекурренты с неприводимым характеристическим многочленом f(x), f(0)0 при ненулевом начальном состоянии равен порядку многочлена f(x).

Данная теорема показывает, как для генерации последовательностей максимального периода можно использовать примитивные многочлены.

3.3.12. Задания

1. Выяснить, обладают ли свойствами ассоциативности и коммутативности операции  на множестве А, если

A=N, xy=x+2y; A=N, xy = x^y;

A=N, xy=3xy; A=N, xy =НОД(x,y);

A=Z, xy=x – y; A=Z, xy = x²+ y²;

A=R, xy = sinxcosy; A=R, xy = x^y.

2. Какие из указанных числовых множеств являются группами относительно заданных операций:

1) множество степеней данного вещественного числа с целыми показателями относительно умножения;

2) множество комплексных чисел с фиксированным модулем относитель­но операции умножения;

3) множество положительных действительных чисел относительно операции умножения;

4) отрезок [0,1] относительно операции умножения;

5) отрезок [0,1] относительно операции  = {+};

6) корни всех степеней из единицы относительно умножения?

3. Какие из указанных множеств квадратных матриц фиксированного поряд­ка образуют группу относительно операции умножения:

1) множество симметрических матриц с вещественными элементами;

2) множество невырожденных матриц с вещественными элементами;

3) множество целочисленных матриц с определителем, равным ±1;

4) множество верхних треугольных матриц с вещественными элементами;

5) множество ортогональных матриц;

6) множество диагональных матриц?

4. Доказать, что множество функций вида у =(ах + b)(сх + d)^-1, где a,b, с, d R, ad–bc0, является группой относительно операции композиции функций.

5. Доказать, что если в группе G выполнено условие х² = е, х  G, то группа G коммутативна.

1. Доказать, что в любой группе (ab)^-1 =b^-1а^-1 и вообще

(a₁a₂…a_n) ^-1 =a_n^-1a_n-1^-1…a₁^-1.

7. Доказать, что множество всех квадратных матриц данного порядка, в каждой строке и каждом столбце которых один элемент равен 1, а остальные 0, образует группу.

8. Составить таблицу Кэли для циклической группы пятого порядка.

9. Найти с точностью до изоморфизма вес группы порядков 3,4, 6. Составить их таблицы Кэли.

10. Доказать, что в конечной группе любое подмножество Н, замкнутое по умножению (h₁,h₂H h₁h₂H ), будет подгруппой.

11. Доказать, что для нетривиального смежного класса gH(egH) выполняется условие h₁,h₂gH h₁h₂H.

12. Доказать, что пересечение двух подгрупп будет подгруппой.

13. Показать, что в любой группе подстановок, содержащей хотя бы одну нечетную подстановку, количество четных подстановок равно количеству нечетных.

14. Найти все подгруппы групп S₆,Z₆,Z₂₄.

15. Разложить:

1) аддитивную группу вещественных чисел по подгруппе целых чисел;

2) аддитивную группу комплексных чисел по подгруппе целых гауссовских чисел;

3) симметрическую группу S_n по подгруппе подстановок, оставляющей элемент 1 на месте;

4) группу Z₆ по своим подгруппам;

5) группу S₃ по своим подгруппам.

16. Пусть a G. Доказать, что множество элементов {х | ха = ах, хG}, называемое централизатором элемента а, является подгруппой.

17. Доказать, что множество элементов {х | ха = ах, хG}, называемое централизатором группы, является нормальной подгруппой.

18. Найти централизаторы элементов

в группе GL(2,R).

19. Найти центр группы GL(2,R).

20. Показать, что порядки элементов а и а^-1 равны.

21. Показать, что порядки элементов аb и bа равны.

22. Доказать, что аддитивные группы вещественных и рациональных чисел не являются циклическими.

23. Пусть А и В нормальны в G, AB=e, тогда каждый элемент aA перестановочен с каждым элементом bB.

24. Подгруппа, порожденная элементами вида аbа^-1b^-1 (коммутаторами), называется коммутантом. Доказать, что

1. аbа^-1b^-1= е  аb=bа;

2. К  G;

3) фактор-группа G/K – абелева;

4) если G/ Н – абелева, то К  Н.

25. Определить с точностью до изоморфизма все абелевы группы порядка 8.

26. Пусть Н – подмножество группы G c условием h₁,h₂H h₁h₂H. Доказать, что |Н|  0.5|G|.

27. Вычислить следующие произведения подстановок:

1) (1,2) (1,3) (1,4) (2,3) (3,5);

2) (125) (124) (129);

3) f¹⁰⁰ , где

28. Найти подстановку Х, если АХВ² = С,

29. Доказать, что две подстановки сопряжены тогда и только тогда, когда имеют одинаковое количество циклов каждой длины.

30. Доказать, что в булевом кольце (х² = х):

1) умножение коммутативно;

2) х + х = 0;

3) кольцо не является областью целостности.

31. Доказать, что в определении кольца с единицей не обязательно требовать, чтобы операция «+» была коммутативной.

32. Доказать, что следующие подмножества являются подкольцами в кольце М_п(R):

1) диагональные матрицы;

2) верхнетреугольные матрицы.

33. Найти все подкольца колец вычетов Z₇, Z₁₀, Z₁₂.

34. Может ли в кольце, не являющемся полем, содержаться некоторое поле?

35. Показать, что эндоморфизмы абелевой группы образуют кольцо.

36. Показать, что биекция а+b2  а+b3 не является изоморфизмом полей Q(2),Q(3) и что эти поля вообще неизоморфны.

37. Докажите, что Q(2 + 3) = Q(2 – 3) = Q(2, 3).

38. Установить, что I – идеал кольца К. Является ли фактор-кольцо полем?

1) К ={а+bi | а,bZ}, I ={а + bi | a,b 3Z}.

2) K={a+ b2| a,bZ,}, I ={a + b2| a,b3Z}.

3) K=Z₃[x], I=(x² +1).

4) K=Z₂[x], I=(x² + х).

5) K=R[x], I=(x² +1).

39. Найдите идеал, порожденный множеством М, если

1) М ={3,5} в кольце Z;

2) М ={4,10} в кольце Z;

3) М ={х⁶–1,х⁴–1} в кольце R[x];

4) М ={х, х + 1} в кольце R[x].

40) Доказать, что фактор-кольцо R[x]/(x⁴ + x³ + х +1) не может быть полем ни для какого коммутативного кольца R.

41) Вычислить образ (2х + 1)^-1 в фактор-кольце F[x]/(x³ – 2), где

1) F=Q;

2) F=Z₅;

3) F=F₇.

42. Доказать, что (x^m –1) |(xⁿ – 1)  m |n над любым полем коэффициентов.

43. Является ли С[0,1] областью целостности? Показать, что отображение ff(а) является эпиморфизмом, а ядро – максимальным идеалом.

44. Показать, что если р(х) приводим, то идеал (р(х)) немаксимален.

45. Показать, что х² + х + 1, х³ + х + 1, х⁴ + х + 1 неприводимы над F₂ и что нет других неприводимых многочленов 2-й и 3-й степени.

46. Составить таблицы умножения и сложения для колец Z₂[x]/(х² + х + 1), Z₂[x]/(х³ +х+1), Z₂[x]/( х³ + х² + 1).

47. Применив алгоритм Евклида, найти наибольшие общие делители многочленов с коэффициентами из поля F:

1) F=F₂, х⁷ + 1, х⁵ + х³ + 1;

2) F=F₂, х⁵ +x+ 1, х⁶ + х⁵ + х⁴ + 1;

3. F=F₃, х⁸ + 2х⁵ + х³ + х² + 1, 2х⁶ + х⁵ + 2х³ + 2х² + 1;

48. Вычислить f(3), если f(х)=х²¹⁴ + 3х¹⁵² + 2х⁴⁷ + 2 F₅[x].

49. Решить, если возможно, сравнения:

1) (х² + 1)f(х) = l(mod(x³ + 1)) в F₃[х];

2) (х⁴ + х³ + х² + 1)f(х) = х² + l(mod(x³ + 1)) в F₂[х].

50. Пусть f(х)  F_p[x], тогда (f(x))^p= f(x^p). Доказать.

51. Доказать, что в коммутативном кольце характеристики р

Доказать неприводимость многочленов х² +1, х² + х + 4 над полем F₁₁ и построить изоморфизм фактор-колец

F₁₁[x]/(x² + 1)  F₁₁[x]/(x² + x + 4).

52. Найти порядки многочленов: х¹⁰ + x⁹ + x³ + x² F₂[x],

х⁸ + х⁷ + х³ + х + 1 F₂[x], x⁷ + х⁶ + x⁴ – х² + х F₃[x],

(x² + х + l)⁵ (х³ + х + 1) F₂[x]. Какие из них неприводимы?

53. Найти примитивный многочлен степени 6 над полем F₂.

54. Найти примитивный элемент  в Z[x]/(x² - 2), представить степени ²,...,⁸ в виде а + b2, a, b F₃. Однозначно ли такое представление?

55. Можно ли вложить F₄ в F₈?

56. Найти все примитивные элементы полей F₇, F₉, F₁₇.

57. Найти базис поля F₂₅ над простым подполем. Разложить все элементы по этому базису. Найти примитивный элемент  этого поля и для любого эле­мента  F₂₅ найти п такое, что  = ^п.

58. Доказать, что если I – идеал кольца К, то I[x] – идеал кольца К[х].

59. Показать, что элемент 2 +i имеет степень 4 над Q и степень 2 над R. Найти его минимальные многочлены.

60. Доказать, что если многочлен F(х) неприводим в F_q[x], то F(aх+b) также неприводим, где a,b F_q , a0,

61. Разложить многочлены на неприводимые множители: х⁹ + х+1 над F₂,

х⁷ + х⁶ + х⁵ – х³ + х² –х–1 над F₃.

62. С помощью матриц дать представление для элементов поля F₈, используя многочлен х³ + х + 1. Дать аналогичное представление для F₁₆, F₉.

63. Доказать неприводимость многочлена х⁴ + х + 1 над F₂ и построить таблицы операций для его поля корня.

64. Показать, что поле корня х³ + х +1 над F₂ есть поле разложения.

65. Найти поля разложения (х² –3)(х³ +1) над Q, (х² –3)(х² –2х–2) над Q,

х³ + х + 1 над F₂.

66. Найти изоморфизм полей разложения х³ + 2х + 1 и х³ + 2х + 2 над F₃.

67. Найти степени неприводимых множителей многочлена х¹⁷ – 1 над F₂ и его поле разложения.

68. Установить примитивность многочленов x⁶ +x⁵+ x² +х+1 над F₂, x⁵ – х+1 над F₃.

69. Найти хотя бы один примитивный многочлен степени 3 над полем F₄.

70. Установить неприводимость, примитивность и найти порядок

х⁴ + х³ + х² – х – 1 над полем F₃.

68. Пусть A – любое множество автоморфизмов поля F. Показать, что элементы, инвариантные относительно всех а  А, образуют подполе S(A) F.

69. Над нолем F₂ рассматривается рекуррентное уравнение s_i – s_i-2 + s_i-3 =0. Вычислить периоды всех 8 последовательностей и их внутрипериодные значения.

70. Построить регистр сдвига с обратной связью, реализующий соотношение из предыдущею задания.