4.4.3. Блочные шифры простой замены

Как мы убедились, задача вскрытия простой однобуквен­ной замены является не слишком сложной. Основная слабость такого шифра состоит в том, что избыточность открытого текста, полностью проникающая в шифртекст, делает (за счет малого числа шифрвеличин, которыми являются буквы алфавита) очень рельефной диаграмму повторяемости знаков криптограммы. Это побудило в свое время криптографов к устранению этой слабости за счет увеличения числа шифрвеличин. Интуитивно понятно, что чем больше разница между числом шифрвеличин и числом букв алфавита, тем более рав­номерной должна стать диаграмма повторяемости знаков шифртекста. Первым естественным шагом в этом направле­нии стало увеличение значности шифрвеличин, то есть ис­пользование блочных шифров простой замены.

Простейший блочный шифр оперирует с биграммными шифрвеличинами. Одними из первых таких шифров были биграммные шифры Порта и Плейфера. Приведем описание шифра Плейфера, нашедшего широкое применение в начале ХХ века.

Основой шифра Плейфера является прямоугольная таблица, в которую записан систематически перемешанный алфавит (для удобства запоминания). Правило зашифрования состоит в следующем.

Буквы биграммы (i, j), i  j (являющейся шифрвеличиной) находятся в данной таблице. При зашифровании биграмма (i, j) заменяется биграммой (k,l), где k и l опреде­ляются в соответствии с правилами 1-3.

1. Если i и j не лежат в одной строке или одном столбце, то их позиции образуют противоположные вершины прямоугольника. Тогда k и l – другая пара вершин, причем k – вершина, лежащая в той же строке, что и i.

2. Если i и j лежат в одной строке, то k и l – буквы той же строки, расположенные непосредственно справа от i и j соответственно. При этом если одна из букв – последняя в строке, то считается, что ее "правым соседом" является пер­вая буква той же строки.

3. Аналогично, если i и j лежат в одном столбце, то они заменяются их "соседями снизу".

При зашифровании открытый текст представляется в ви­де последовательности биграмм. Если текст имеет нечетную длину или содержит биграмму, состоящую из одинаковых букв, то в него добавляются "пустышки" следующим образом. "Пустышкой" является некоторая редкая для данного типа текста буква (или знак), которая вставляется между одинаковыми буквами биграммы или добавляется в текст для того, чтобы его длина стала четной. Такие изменения открытoго текста, как правило, не мешают при расшифровании. Проиллюстрируем сказанное следующим примером.

Пример (шифра Плейфера)

Пусть шифр использует прямоугольник размером 5 х 6, в который записан систематически перемешанный русский 30-буквенный алфавит на основе ключевого слова командир:

к	о	м	а	н		д
и	р	б	в		г	е
ж	з	л	п		с	т
у	ф	х	ц		ч	ш
щ	ь	ы	э		ю	я

Зашифруем фразу "автором метода является Уитстон". В качестве "пустышки" будем использовать редкую букву ф. Представим фразу в виде последовательности биграмм:

АВ ТО РО МФ ME ТО ДА ЯВ ЛЯ ЕТ СЯ УИ ТС ТО НФ

(Нам пришлось дважды вставить "пустышку".)

В соответствии со сформулированными правилами получаем шифртекст:

ВП ЗД ЗР ОХ ДБ ЗД КН ЭЕ ТЫ ТШ ШД ЩЖ ЖТ ЗД ОЧ или без пробелов

впздзрохдбздкнэетытшшдщжжтздоч

Криптоанализ шифра Плейфера опирается на частотный анализ биграмм, триграмм и четырехграмм шифртекста и особенности замены шифрвеличин на шифробозначения, свя­занные с расположением алфавита в прямоугольнике. При этом существенную информацию о заменах дает знание того, что используется систематически перемешанный алфавит.

Шифрвеличинами для другого широко известного блоч­ного шифра – шифра Хилла (названного по имени Лестора Хилла) – являются п-граммы открытого текста (п > 1), представленного некоторым числовым кодом (так что алфа­витом открытого текста служит кольцо вычетов по модулю мощности алфавита Z_m).

Правило зашифрования представляет собой линейное преобразование кольца Z_m : если х=(х₁,...,х_n) – n-грамма открытого текста, k =(k_ij) – некоторая обратимая матрица над Z_m (ключ) и y=(y₁,...,y_n) – n-грамма шифртекста, то у=Е_k(х) = k • х. Соответственно х =D_k (у) = k ^-1• у,

где k ^-1 – матрица, обратная к матрице k.

Подчеркнем, что матричные операции здесь производятся над кольцом Z_m.

Проиллюстрируем введенное определение примером.

Пример (шифра Хилла)

Положим п = 4 и зашифруем фразу:

без труда не вынешь рыбку из пруда

записанную в 30-буквенном русском алфавите. Условимся о числовом кодировании букв в соответствии с таблицей:

А	Б	В	Г	Д	Е	Ж	З	И	К	Л	М	Н	О	П
1	18	11	6	0	15	20	5	21	23	13	4	16	8	25

Р	С	Т	У	Ф	X	Ц	Ч	Ш	Щ	Ь	Ы	Э	Ю	Я
24	10	19	26	12	2	28	7	17	22	3	29	27	14	9

В качестве ключа выберем матрицу

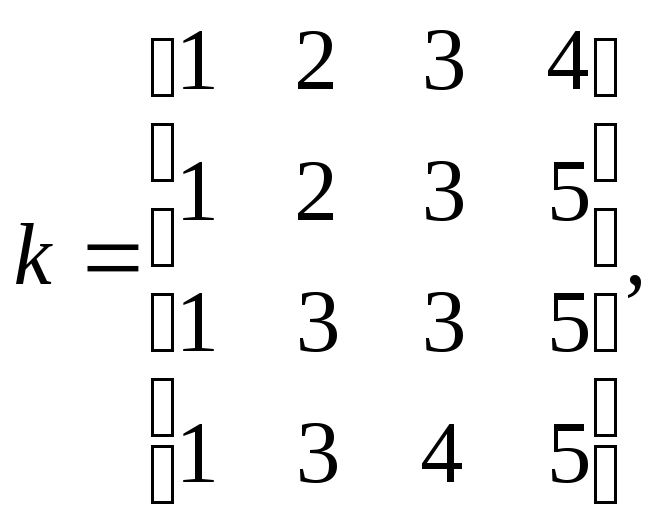
являющуюся обратимой над кольцом Z₃₀. Несложно убедиться в том, что

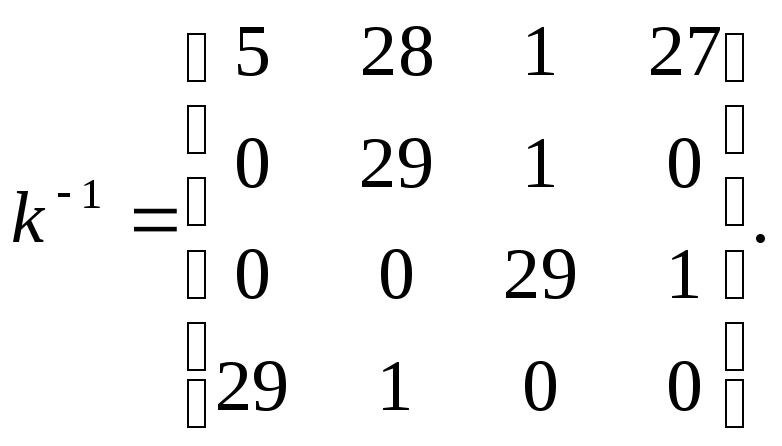
Запишем открытый текст по столбцам матрицы Т :

и получим шифртекст в виде столбцов матрицы k • Т:

Теперь осталось воспользоваться числовым кодом, чтобы выписать шифртекст в буквенном виде:

токцжишшеюыстщчрбвсцьцтржишш

Замечание. Из соображений удобства в применении по­лучили широкое распространение шифры, для которых пра­вила зашифрования и расшифрования идентичны. Такие шифры называются обратимыми. Шифр Хилла является об­ратимым в том и только том случае, когда k ^-1= k, или иначе: k² = Е, где Е – единичная матрица. Матрица, удовлетво­ряющая этому свойству, называется инволютивной.

Из курса алгебры известен критерий обратимости квад­ратной матрицы над кольцом Z_m.

Теорема. Квадратная матрица М над кольцом Z_m об­ратима тогда и только тогда, когда (М,т)=1, то есть определитель М взаимно прост с т.

Заметим, что правило зашифрования Е_М (с матрицей М_nn) в шифрсистеме Хилла является обратимым линейным преобразованием n-мерного модуля

. Такая функция является лишь одним из примеров простого задания обратимого преобразования —> , являющегося, очевидно, биекцией на . Любая же такая биекция потенциально может рас­сматриваться как правило зашифрования блочного шифра простой замены (если п – размер блока), выбираемого некоторым ключом. Поскольку число обратимых линейных преобразований модуля составляет (при n >2, m >2) лишь незначительную часть общего числа рассматриваемых биекций, то же самое можно сказать и о доле, которую составляют (при данном п) шифрсистемы Хилла в множестве возможных блочных шифров простой замены.

Естественным обобщением шифра Хилла является аф­финный блочный шифр, правило зашифрования Е_(А,b)(х) которого определяется формулой:

Е_(А,b)(х)=хА+ b.

При этом А является "обратимой п х п матрицей, а b – фиксированным п-мерным вектором над Z_m.

Как и при рассмотрении предыдущих шифров, приведем некоторые соображения о криптоанализе аффинного блочного шифра и, в частности, шифра Хилла.

Увеличение значности шифрвеличин резко усложняет попытки вскрытия открытого текста по известному тексту криптограммы. Однако свойство линейности, присущее рассматриваемым шифрам, конечно, является их криптографиче­ской слабостью. Чтобы показать это, рассмотрим следующую криптоатаку на аффинный шифр.

Предположим, что известны п+1 пар блоков открытого текста и соответствующих им блоков шифртекста:

(х₀,у₀),…,(х_n,у_n), х_i, у_i  , полученных на одном ключе (A, b). Требуется этот ключ найти.

Для решения поставленной задачи положим:

x⁽ⁱ⁾=х_i – x₀, y⁽ⁱ⁾=y_i – y₀, i=1,…,n.

Тогда x⁽ⁱ⁾ и y⁽ⁱ⁾ оказываются связанными линейным соот­ношением y⁽ⁱ⁾=х⁽ⁱ⁾А.

А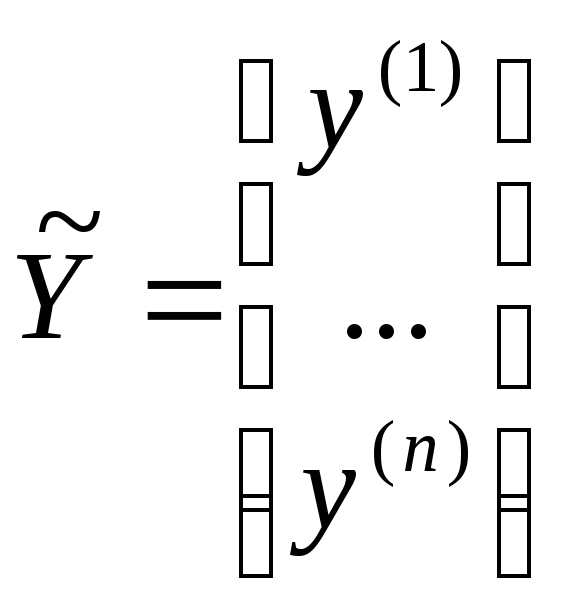налогичное соотношение имеет место и для матриц

и :

из которого находим матрицу А в виде произведения

Наконец, вектор b находится, например, по формуле b = y₀ — х₀•А. Естественно, что такое решение корректно лишь в том случае, когда матрица

обратима.

Поскольку обращение матрицы и вычисление произведе­ния матриц являются не слишком трудоемкими операциями, то таковой же является и поставленная задача.

Более детальное рассмотрение блочных шифров простой замены будет продолжено в Теме 6.