8.3. Шифрсистема Мак-Элиса

Идея, лежащая в основе данной системы, состоит в вы­боре корректирующего кода, исправляющего определенное число ошибок, для которого существует эффективный алго­ритм декодирования. С помощью секретного ключа этот код "маскируется" под общий линейный код, для которого, как известно, задача декодирования не имеет эффективного ре­шения.

В системе Мак-Элиса параметрами системы, общими для всех абонентов, являются целые числа k, п и t. Для получе­ния открытого и соответствующего секретного ключа каждо­му из абонентов системы следует осуществить следующую последовательность действий:

1) выбрать порождающую матрицу G=G_{k n} двоичного (n,k) -линейного кода, исправляющего t ошибок, для кото­рого известен эффективный алгоритм декодирования;

2) случайно выбрать двоичную невырожденную матрицу S = S_{k k} ;

3) случайно выбрать подстановочную матрицу Р = Р_{n n} ;

4) вычислить произведение матриц G₁ = S • G • Р .

Открытым ключом является пара (G₁, t), секретным — тройка (S, G, Р).

Для того чтобы зашифровать сообщение М , предназна­ченное для абонента А, абоненту В следует выполнить сле­дующие действия:

1) представить М в виде двоичного вектора длины k;

2) выбрать случайный бинарный вектор ошибок Z дли­ны п, содержащий не более t единиц;

3) вычислить бинарный вектор С = М • G_A + Z и напра­вить его абоненту А.

Получив сообщение С, абонент А вычисляет вектор С₁ = С • Р^-1, с помощью которого, используя алгоритм деко­дирования кода с порождающей матрицей G, получает далее векторы М₁ и М = М₁ • S^-1.

Чтобы убедиться в корректности приведенного алгоритма расшифрования, достаточно заметить, что

C₁=C•P^-1 =(M•C_A+Z) •Р^-1 =(M•S•G•P+Z)•P^-1 =(M•S) •G+Z•P^-1,

где Z•Р^-1 – вектор, содержащий не более t единиц. Поэто­му алгоритм декодирования кода с порождающей матрицей G декодирует С в М₁ = М • S.

В качестве кода, исправляющего ошибки в системе Мак-Элиса, можно использовать код Гоппы (см., например, [Пит64]). Известно, что для любого неприводимого полинома g(x) степени t над полем GF(2^m) существует бинарный код Гоппы длины п = 2^m и размерности k  п – mt, исправ­ляющий до t ошибок включительно, для которого имеется эффективный алгоритм декодирования. В настоящее время не известны эффективные алгоритмы дешифрования системы Мак-Элиса, использующей код Гоппы, при правильном выборе параметров системы.

Вместе с тем рекомендуемые параметры для этой системы – п=1024, t=38, k>644 – приводят к тому, что открытый ключ имеет размер около 2¹⁹ бит, а длина сообщения увеличивается при шифровании примерно в 1,6 раза, к связи с чем данная система не получила широкого распространения.

8.4. Шифрсистемы на основе "проблемы рюкзака"

''Проблема рюкзака" (или "ранца") может быть сформулирована следующим образом. Пусть задано множество натуральных чисел А={а₁,а₂,...,а_п} и натуральное число S. Требуется установить, имеется ли такое подмножество множества А, сумма элементов которого была бы равна S. Эквивалентной является следующая формулировка: существует ли такой набор чисел х_i{0,1}, in, для которого

Данная проблема получила свое название в связи с тем, что поставленная задача может быть переформулирована также в следующем виде. Имеется набор предметов с известными весами и рюкзак, который может выдержать вес, не превышающий заданной величины. Можно ли выбрать набор предметов для погрузки в рюкзак так, чтобы они в точности имели максимально возможный вес.

"Проблема рюкзака" является весьма сложной, ее решение с полиномиальной сложностью в настоящее время не известно.

Идея построения системы шифрования на основе "про­блемы рюкзака" заключается в выделении некоторого под­класса задач об укладке рюкзака, решаемых сравнительно легко, и "маскировки" задач этого класса (с помощью некото­рого преобразования параметров) под общий случай. Пара­метры подкласса определяют секретный ключ, а параметры модифицированной задачи – открытый ключ. В качестве легко решаемой задачи Р.Меркль и М.Хеллман в 1978г. предложили задачу об укладке "супервозрастающего" рюкзака. Изложим ее суть.

Назовем супервозрастающей последовательность нату­ральных чисел (b₁,b₂,...,b_п), обладающую свойством

Можно убедиться в том, что "проблема рюкзака" для су­первозрастающей последовательности может быть решена с помощью процедуры, состоящей в выполнении следующих шагов:

1. Положить i = п.

2. Если i > 1, то положить х_i равным 1 и S равным S – b_i, если S>b_i, и положить х_i равным 0 в противном случае.

3. Положить i равным i –1 и возвратиться к шагу 2.

В системе, основанной на проблеме рюкзака, величина п является параметром системы.

Для вычисления открытого и соответствующего секрет­ного ключа каждый из абонентов системы осуществляет сле­дующую последовательность действий.

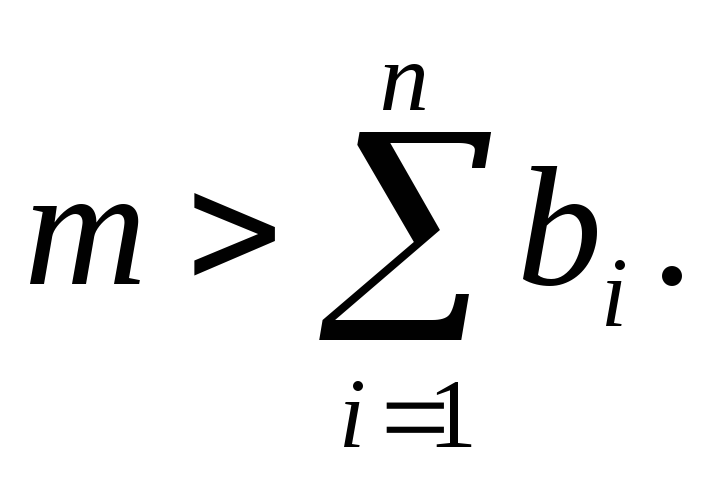1. Выбирает супервозрастающую последовательность (b₁,b₂,...,b_п) и модуль т, такой, что

2. Выбирает случайное число W, 1<W <т-1, такое, что Н0Д(W,m)=1.

3. Выбирает случайную перестановку л чисел {1,2,...,n}.

4. Вычисляет a_i=W b_(i) mod m для i = 1,…,п.

Открытым ключом является набор (а₁,а₂,...,а_п), секретным ключом – набор (,m,W,(b₁,b₂,...,b_п)).

Чтобы зашифровать сообщение М, предназначенное для абонента А, абонент В осуществляет следующие шаги с помощью открытого ключа (а₁,а₂,...,а_п) абонента А:

1. Представляет М в виде бинарной последовательности М=М₁М₂...М_п длины п.

2. Вычисляет С = и направляет его к А.

Абонент А, получив С, вычисляет Н =W^-1•C mod m, a затем, решая "проблему рюкзака" для супервозрастающей " последовательности, находит числа z_i {0,1}, такие, что

Биты последовательности М вычисляются по формуле

М_i= z_(i) , i = 1,…,п.

Корректность проведенной процедуры расшифрования вытекает из следующих рассуждений. Поскольку

и 0 < Н < т, то Н= и, следовательно, алгоритм решения "проблемы рюкзака" действительно находит биты открытого текста, переставленные в соответствии с переста­новкой л.

Вместе с тем доказано, что существует алгоритм полино­миальной сложности, который может быть использован про­тивником для получения открытого текста М по шифртексту С. Этот алгоритм, исходя из а_i , находит пару таких целых чисел и₁ , т₁, что отношение и₁ /т₁ близко к отношению и/т

(где u=W^-1modm, a W,m являются частью секретного ключа). Кроме того, числа В_i=u_i•a_i(modm), 1<i<n, обра­зуют супервозрастающую последовательность. Эта последо­вательность затем используется противником вместо (b₁,b₂,...,b_п) для дешифрования сообщения.

Контрольные вопросы

1. В чем состоят преимущества систем с открытыми ключа­ми перед симметричными шифрсистемами?

2. Сложностью какой математической задачи определяется стойкость системы RSA?

3. К какому типу принадлежит схема шифрования, исполь­зуемая в системе Эль-Гамаля? В чем ее преимущества?

4. Чем вызваны трудности в практической реализации сис­темы Мак-Элиса?

5. Придумайте алгоритм вычисления а^d(тоd п), имеющий сложность 0(ln п).

6. Постройте пример шифра Эль-Гамаля для р = 127. За­шифруйте и расшифруйте выбранное Вами т  126.

Литература

1. А.В. Аграновский. Р.А. Хади. Практическая криптография. М., Солон-Р, 2002.

2. Алфёров, А.П., Зубов, А.Ю., Кузьмин, А.С., Черёмушкин, А.В. Основы криптографии. -М.: Гелиос АРВ, 2005.

3. Андрончик, А. Н. и др. Защита информации в компьютерных сетях. Практический курс: учебное пособие / А. Н. Андрончик, В. В. Богданов, Н. А. Домуховский, А. С. Коллеров, Н. И. Синадский, Д. А. Хорьков, М. Ю. Щербаков; Под ред. Н. И.Синадского – Екатеринбург: ГОУ ВПО УГТУ - УПИ, 2008. – 246 с.

4. Анохин М. И., Варновский Н. П., Сидельников В. М., Ященко В. В. Криптография в банковском деле. —М.: Изд-во МИФИ, 1997.

5. Аршинов М. Н., Садовский Л. Е. Коды и матема­тика. — М.: Наука, 1983.

6. А.В. Бабаш, Г.П. Шанкин. Криптография. М., Солон-Р, 2002.

7. А.П. Баранов, Н.П. Борисенко, П.Д. Зегжда, С.С. Корт, А.Г. Ростовцев "Математические основы информационной безопасности" .

8. С. Баричев, Р. Серов "Основы современной криптографии"

9. A.A-Большаков, А.Б. Петряев, В.В. Платонов, Л.М. Ухлинов. "Основы обеспечения безопасности данных в компьютерных системах и сетях. Часть 1. Методы, средства и механизмы защиты данных", ВИККА им. Можайского, СПБ, 1995.

10. Брассар Ж. Современная криптология. М.: Полимед, 1999.

11. Бейкер А. Введение в теорию чисел. Мн.: Вышэйш. шк., 1995.

12. Березин Б. В., Дорошкевич П. В. Цифровая под­пись на основе традиционной криптографии // Защита информации.— 1992.— Вып. 2.— С.148—167.

13. Болл У., Коксетер Г. Математические эссе и развлечения (криптография и криптографиче­ский анализ). —М.; Мир, 1986.

14. Брассар Ж. Современная криптология. — М.:Полимед,1999.

15. Варфоломеев А. А., Пеленицын М. Б. Методы криптографии и их применение в банковских технологиях. — М.: Изд-во МИФИ, 1995.

16. Варфоломеев А. А., Жуков А. Е., Пудовкина М. А. Поточные криптосистемы. Основные свойства и методы анализа стойкости. — М.: Изд-во МИФИ, 2000.

17. Варфоломеев А. А., Домнина О. С., Пелени­цын М. Б, Управление ключами в системах криптографической защиты банковской инфор­мации. — М.: Изд-во МИФИ, 1996.

18. Введение в криптографию / Под ред. В.В. Ященко. М.: МЦНМО, 2001.

19. М. Вельшенбах. Криптография на Си и C++ в действии. Под редакцией П.В. Семьянова. М., Триумф, 2004.

20. Гайкович В., Першин А. Безопасность электрон­ных банковских систем.— М.: Единая Европа, 1994.

21. Герасименкo В.А., Малюк A.A. Основы защиты информации: Учеб. пособие. М.:МИФИ, 1997.

22. Диффи У., Хеллман М. Э. Защищенность и имитостойкость. Введение в криптографию // ТИИЭР. — 1979. — Т. 67. — № 3.

23. Духан, Е. И. Применение программно-аппаратных средств защиты компьютерной информации: учеб. пособие / Е. И. Духан, И. Н. Синадский, Д. А. Хорьков. – Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2007. – 174 с.

24. Жельников В. Криптография от папируса до компьютера. М.: ABF, 1996.

25. Зубов, А.Ю. Криптографические методы защиты информации. Совершенные шифры. -М.: Гелиос АРВ, 2005.

26. Дэвид Кан. Взломщики кодов. - М.: Центрполиграф, 2000.

27. Д.Кан "Разведчики и цензура"

28. Нил Коблиц, Курс теории чисел и криптографии, М. ТВП, 2001

29. Конхейм А. Г. Основы криптографии. — М.: Ра­дио и связь, 1987.

30. Кузьминов Т. В. Криптографические методы за­щиты информации. — Новосибирск: Наука, 1998.

31. Лидл Р., Нидеррайтер Г. Конечные поля: В 2 т. М.: Мир, 1988.

32. Мельников В.В. Защита информации в компьютерных системах. М.: Финансы и статистика, 1997.

33. Молдовян Н.А. Проблематика и методы криптологии. СПб.: Изд-во СПбГУ, 1998.

34. Молдовян Н.А. Скоростные и блочные шифры. СПб.: Изд-во СПбГУ, 1998.

35. А.А. Молдовян, Н.А. Молдовян, Б.Я. Советов. Криптография. М.. Лань, 2001.

36. МэссиДж.Л. Современная криптология: введе­ние // ТИИЭР. — 1988. — Т. 76. — № 5.

37. Нечаев В.И. Элементы криптографии. Основы теории защиты информации. М.: Высш. шк., 1999.

38. Ноден П., Китте К. Алгебраическая алгоритмика. М.: Мир, 1999.

39. ОрловВ.А., Филиппов Л.И. Теория информации в упражнениях и задачах. М.: Высш. шк., 1976.

40. Петров А. А. Компьютерная безопасность. Криптографические методы защиты. — М.:ДМК, 2000.

41. Романец Ю.В., Тимофеев П.А., Шаньгин В.Ф. Защита информации в компьютерных системах и сетях. -М.: Радио и связь, 1999.

42. Ростовцев А.Г., Матвеев В.А. Защита информации в компьютерных системах. Элементы криптологии. Под редакцией П. Д. Зегжды. Издание СПбГТУ, 1993.

40. Ростовцев А.Г. Алгебраические основы криптографии. СПб, Мир и Семья, 2000.

41. Ростовцев А.Г.. Маховенко Е.Б. Введение в криптографию с открытым ключом. СПб, Мир и Семья, 2001.

42. Саломаа А. Криптография с открытым клю­чом.—М.:Мир, 1996.

43. Сачков В.Н, Введение в комбинаторные методы дискретной математики. М.: Наука, 1982.

44. Сингх, С. Книга шифров. Тайная история шифров и их расшифровки. -М.: АСТ - Астрель, 2006.

45. Словарь криптографических терминов. Под ред. Погорелова Б.А., Сачкова В.Н. -М.: МЦНМО, 2006.

46. Соболева Т. А. Тайнопись в истории России. Ис­тория криптографической службы России XVIII-начала XX в. -М.: Международные отношения, 1994.

47. Столлингс В. Криптография и защита сетей. Принципы и практика. -М.: Изд. Дом "Виль­яме" 2-е изд., 2001.

48. Утешев А.Ю., Черкасов Т.М.. Шапошников А.А. Цифры и шифры. СПб.: Изд-во СПбГУ. 2001.

49. Фомичёв, В.М. Дискретная математика и криптология. 2-е изд. -М.: “ДИАЛОГ-МИФИ”, 2009.

50. Харин Ю.С., Агиевич С.В. Компьютерный практикум по математическим методам защиты информации. Мн.: БГУ, 2001.

51. Харин Ю.С., Берник В.И., Матвеев Г.А. Математические основы криптологии. Мн.: БГУ, 1999.

52. Хинчин А.Я. Цепные дроби. M.: Физматгиз, 1964.

53. Хоффман Л. Современные методы защиты информации. – М.:Мир,1970.

54. А.Чмора. Современная прикладная криптография. М., Гелиос, 2002.

55. Шеннон К. Теория связи в секретных системах//В кн.: Работы по теории информации и кибернетике.- М.: ИЛ,1963.

56. Брюс Шнайер. Прикладная криптография, 2-е издание: протоколы, алгоритмы. исходные тексты на языке Си. Под редакцией П.В. Семьянова. М., Триумф, 2002.

• Периодические издания

журнал "Защита информации. Конфидент"

журнал "Проблемы информационной безопасности. Компьютерные системы"

ИНТЕРНЕТ-ИСТОЧНИКИ

А. В. Бабаш, Г.П. Шанкин, Криптография, 2007, 511 стр., DJVU, 9.5 мб

http://ifolder.ru/19035938

Панасенко Сергей, Алгоритмы шифрования. Специальный справочник. 2009 г., 576 стр., djvu, 7,41Mb

http://ifolder.ru/14970991

Московский Государственный Технический Университет им. Н.Э. Баумана, Кафедра ИУ-8, Жуков А.Е. Системы блочного шифрования. Пособие по курсу «Криптографические методы защиты информации»

http://stream.ifolder.ru/13203588

Московский Государственный Технический Университет им. Н.Э. Баумана, Кафедра ИУ-8, Жуков А.Е. Системы поточного шифрования. Пособие по курсу «Криптографические методы защиты информации»

http://stream.ifolder.ru/13203676

Практическая Криптография, Нильс Фергюсон, Брюс Шнайер, Изд. Вильямс, 2005,416 стр.

http://www.onlinedisk.ru/file/41482/

"Handbook of Applied Cryptography".

http://www.cacr.math.uwaterloo.ca/hac/

100