8.1. Шифрсистема rsa

Система RSA была предложена в 1978 г. и в настоящее время является наиболее распространенной системой шифрования с открытым ключом. Напомним ее определение, приведенное в Теме 1 (определение 4).

Пусть п = р • q — целое число, представимое в виде произведения двух больших простых чисел p,q. Выберем числа е и d из условия

е•d1(mod (n)), (8.1)

где (п) = (р – 1) • (q–1) – значение функции Эйлера от числа п. Пусть k=(n,p,q,e,d) – выбранный ключ, состоящий из открытого ключа k_з =(n,e) и секретного ключа k_р = (n,p,q,d). Пусть М – блок открытого текста и С – соответствующий блок шифрованного текста. Тогда правила зашифрования и расшифрования определяются формулами:

С = Е_k(М) = M^е(mod n), D_k(C) = C^d(mod n) . (8.2)

Заметим, что в соответствии с (2) D_k(С) = М. Это выте­кает из следующих рассуждений. Для любого целого числа М и любого простого р справедливо сравнение

М ^р  M(mod р). (8.3)

В самом деле, (8.3) равносильно сравнению

М^р – M  0(mod р)

или сравнению

M( М^р-1 – 1)  0(mod р) (8.4)

Если НОД(М,р)=р, то р делит М, и поэтому М  0(mod p), откуда следует (8.4). Если же НОД(М,р) = 1, то, согласно малой теореме Ферма, М^р-1l(modp), откуда также следует (8.4).

Согласно (8.1), существует целое число r, такое, что e d = r(п)+ 1. Отсюда и из (8.3) получаем следующую це­почку равенств и сравнений:

С ^d =(M^e)^d =M^ed = М^{r(п)+ 1}=M^r•^(p-l)(q-l)+l = M^r•^p(q-l)M^-r•^q+r+l =

= M^r•^(q-l)M^-r•^q+r+l) = M^r•^(q-l) M^-r•^(q+r+l  M(mod р). (8.5)

Аналогично можно показать, что

С ^d = M(mod р). (8.6)

Поскольку р и q — разные простые числа, то на основании известных свойств сравнений из (8.5), (8.6) получаем:

С ^d = M(mod n).

Отсюда и следует корректность определения (8.2). Для того чтобы лучше представить себе технические детали, возникающие при зашифровании и расшифровании, приведем пример работы с RSA.

Пример

Зашифруем аббревиатуру RSA, используя р=17, q=31. Для этого вычислим n=pq=527 и (п) = (p–1)(q –1) =480 . Выберем, далее, в качестве е число, взаимно простое с (п), например е = 7. С помощью алгоритма Евклида найдем целые числа и и v, удовлетворяющие соотношению eu+(n)v =1:

480=768+4,

7=41+3,

4=31+1,

1=4–31=4–(7–41)1=42–71=(480–768)•2–71=4802–7137,

v=2, и= –137.

Поскольку –137 = 343(mod 480), то d = 343. Проверка:

7343=2401=l(mod 480).

Теперь представим данное сообщение в виде последова­тельности чисел, содержащихся в интервале 0,…,526. Для этою буквы R,S и А закодируем пятимерными двоичными векто­рами, воспользовавшись двоичной записью их порядковых номеров в английском алфавите:

R = 18 = (10010), S =19= (10011), А = 1 = (00001).

Тогда RSA= (100101001100001). Укладываясь в заданный интервал 0,…,526, получаем следующее представление:

RSA=(100101001),(100001)=(M₁ = 297, М₂ = 33).

Далее последовательно шифруем М₁ и М₂:

С₁ = Е_k(М₁) = M₁^e = 297⁷ (mod 527) = 474.

При этом мы воспользовались тем, что

297⁷ =((297²)³297)(mod 527)=((200³(mod 527)297)(mod 527),

С₂ = Е_k(М₂ )= М₂^e = ЗЗ⁷ (mod 527) = 407.

В итоге получаем шифртекст: у₁ = 474, у₂ = 407.

При расшифровании нужно выполнить следующую по­следовательность действий. Во-первых, вычислить

D_k(C₁)=(C₁)³⁴³(mod 527).

Отметим, что при возведении в степень удобно восполь­зоваться тем, что 343 =256+64+16+4+2+1. На основа­нии этого представления получаем:

474² = 174(mod 527), 474⁴(mod 527) = 237, 474⁸ (mod 527) = 307,

474¹⁶ (mod 527) = 443, 474³² (mod 527) = 205, 474⁶⁴ (mod 527) = 392,

474¹²⁸ (mod 527) = 307, 474²⁵⁶ (mod 527) = 443,

в силу чего

474³⁴³ (mod 527) = (443 • 392 • 443 • 237 • 174 • 474)(mod 527) = 297.

Аналогично

407³⁴³ (mod 527) =33.

Возвращаясь к буквенной записи, получаем после рас­шифрования RSA.

Проанализируем вопрос о стойкости системы RSA. Нетрудно показать, что сложность нахождения секретно­го ключа системы RSA определяется сложностью разложения числа п на простые множители. В связи с этим нужно выбирать числа р и q таким образом, чтобы задача разложения числа п была достаточно сложна в вычислительном плане. Для этого рекомендуются следующие требования:

1) числа р и q должны быть достаточно большими, не слишком сильно отличаться друг от друга и в то же время быть не слишком близкими друг другу;

2) числа р и q должны быть такими, чтобы наибольший общий делитель чисел р–1 и q– 1 был небольшим; жела­тельно, чтобы НОД(р–1, q–1) = 2 ;

3) р и q должны быть сильно простыми числами (силь­но простым называется такое простое число r, что r+1 имеет большой простой делитель, r-1 имеет большой про­стой делитель s, такой, что число s – 1 также обладает доста­точно большим простым делителем).

В случае когда не выполнено хотя бы одно из указанных условий, имеются эффективные алгоритмы разложения п на простые множители.

В настоящее время самые большие простые числа, вида п = р • q, которые удается разложить на множители известными методами, содержат в своей записи 140 десятичных знаков. Поэтому, согласно указанным рекомендациям, числа р и q в системе RSA должны содержать не менее 100 деся­тичных знаков.

Следует подчеркнуть необходимость соблюдения осто­рожности в выборе модуля RSA (числа п) для каждого из корреспондентов сети. В связи с этим можно сказать следую­щее.

Самостоятельно можно убедиться в том, что, зная одну из трех величин: р, q или (п), можно легко най­ти секретный ключ RSA. Известно также, что, зная секретную экспоненту расшифрования d, можно легко разложить мо­дуль п на множители. В этом случае удается построить веро­ятностный алгоритм разложения п. Отсюда следует, что ка­ждый корреспондент сети, в которой для шифрования исполь­зуется система RSA, должен иметь свой уникальный модуль.

В самом деле, если в сети используется единый для всех модуль п, то такая организация связи не обеспечивает кон­фиденциальности, несмотря на то, что базовая система RSA может быть стойкой. Выражаясь другими словами, говорят о несостоятельности протокола с общим модулем. Несостоятельность следует из того, что знание произвольной пары экспонент (e_i,d_i) позволяет, как было отмечено, разложить п на множители. Поэтому любой корреспондент данной сети имеет возможность найти секретный ключ любого другого корреспондента. Более того, это можно сделать даже без разложения п на множители.

Как отмечалось ранее, системы шифрования с открытыми ключами работают сравнительно медленно. Для повышения скорости шифрования RSA на практике используют малую экспоненту зашифрования.

Если выбрать число е небольшим или таким, чтобы в его двоичной записи было мало единиц, то процедуру шифрова­ния можно значительно ускорить. Например, выбрав е=3 (при этом ни р–1, ни q–1 не должны делиться на 3), мы можем реализовать шифрование с помощью одного возведе­ния в квадрат по модулю п и одного перемножения. Выбрав е = 2¹⁶ +1=65537 – число, двоичная запись которого содержит только две 1, мы сможем реализовать шифрование с помощью 16 возведений в квадрат по модулю п и одного пе­ремножения. Если экспонента е выбирается случайно, то реализация шифрования по алгоритму RSA потребует s возведений в квадрат по модулю п и в среднем s/2 умножений по тому же модулю, где s – длина двоичной записи числа п. Вместе с тем выбор небольшой экспоненты е может привести к негативным последствиям. Дело в том, что у несколь­ких корреспондентов могут оказаться одинаковые экспоненты е.

Пусть, например, три корреспондента имеют попарно взаимно простые модули п₁, п₂, п₃, и общую экспоненту е = 3. Если еще один пользователь посылает им некое цирку­лярное сообщение М, то криптоаналитик противника может получить в свое распоряжение три шифрованных текста y_i М³ (mod n_i), i = 1,2,3. Далее он может найти решение у системы сравнений

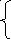y  y₁(mod n₁),

у  y₂(mod n₂),

y  y₃(mod n₃),

лежащее в интервале 0 < у < n₁ • п₂ • n₃. По китайской теореме об остатках такое решение единственно, а так как М³ <n₁ • n₂ • п₃, то у=М³. Само М можно найти, вычисляя кубический корень: М = .

Отметим, что выбор малой экспоненты расшифрования d также нежелателен в связи с возможностью определения d простым перебором. Известно также, что если d < , то экспоненту d легко найти, используя непрерывные дроби.