4.5.5. Криптоанализ шифра Виженера

Рассмотрим шифр модульного гаммирования с уравнени­ем (1), для которого гамма является периодической последовательностью знаков алфавита. Как указывалось ранее, такая гамма обычно получалась периодическим повторением некоторого ключевого слова. Например, ключевое слово KEY дает гамму KEYKEYKEY... . Рассмот­рим задачу вскрытия такого шифра по тексту одной криптограммы достаточной длины.

Пусть  – длина ключевого слова. Обычно криптоанализ шифра Виженера проводится в два этапа. На первом этапе определяется число , на втором этапе – само ключевое слово.

Для определения числа  применяется так называемый тест Казиски, названный в честь Ф. Казиски, применившего его в 1863 г. Тест основан на простом наблюдении того, что два одинаковых отрезка открытого текста, отстоящих друг от друга на расстоянии, кратном , будут одинаково зашифро­ваны. В силу этого в шифртексте ищутся повторения длины, не меньшей трех, и расстояния между ними. Обратим внима­ние на то, что случайно такие одинаковые отрезки могут поя­виться в тексте с достаточно малой вероятностью.

Пусть d₁,d₂,... – найденные расстояния между повторе­ниями и d – наибольший общий делитель этих чисел. Тогда  должно делить d. Чем больше повторений имеет текст, тем более вероятно, что  совпадает с d. Для уточнения значения  можно использовать так называемый индекс сов­падения, введенный в практику У. Фридманом в 1920 г.

Для строки х = (х₁,...,x_m) длины т, составленной из букв алфавита А, индексом совпадения в х, обозначаемым I_c(х), будем называть вероятность того, что две случайно выбранные буквы из х совпадают.

Пусть А = {a₁,...,а_n}. Будем отождествлять буквы алфа­вита с числами, так что а₁  0,..., a_n-1 n — 2, а_n  n — 1.

Теорема. Индекс совпадения в х вычисляется по формуле

(14)

где f_i – число вхождений буквы а_i в х, i Z_n.

Пусть х – строка осмысленного текста. Допустим, как и ранее, что буквы в х появляются на любом месте текста с соответствующими вероятностями р₀,…,p_n-1 независимо друг от друга, где р_i – вероятность появления буквы i в осмысленном тексте, iZ_n. В такой модели открытого текста вероятность того, что две случайно выбранные буквы из х совпадают с iZ_n, равна р_i², следо­вательно,

(17)

Взяв за основу значения вероятностей р_i, приведенные в Приложении 1 для открытых текстов, получим значения индексов совпадения для ряда евро­пейских языков:

Таблица 6. Индексы совпадения европейских языков

Язык	Русский	Англ.	Франц.	Нем.	Итал.	Испан.
Ic(х)	0,0529	0,0662	0,0778	0,0762	0,0738	0,0775

Предположим, что х – реализация независимых испыта­ний случайной величины, имеющей равномерное распределе­ние на Z_n. Тогда индекс совпадения вычисляется по формуле I_c(х)=1/n.

Вернемся к вопросу об определении числа .

Пусть y₁y₂,…,y_m – данный шифртекст. Выпишем его с периодом :

Y1	Y2	…	Y
y1	y2	...	y
y+1	y+2	…	y2
y2+1	y2+2	…	y3

… … … …

и обозначим столбцы получившейся таблицы через Y₁ ,Y₂ ,…,Y_.

Если  – это истинная длина ключевого слова, то каждый столбец Y_{i ,} i1,…,  , представляет собой участок открытого текста, зашифрованный простой заменой.

В силу сказанного выше (для английского языка) I_c(Y_i)= 0,066 при любом i. С другой стороны, если  от­лично от длины ключевого слова, то столбцы Y_i будут более "случайными", поскольку они являются результатом зашифрования фрагментов открытого текста некоторым многоалфа­витным шифром. Тогда I_c(Y_i) будет ближе (для английско­го языка) к числу 1/26=0,038.

Заметная разница значений I_c(х) для осмысленных от­крытых текстов и случайных последовательностей букв (для английского языка – 0,066 и 0,038, для русского языка – 0,053 и 0,030) позволяет в большинстве случаев установить точное значение  .

Предположим, что на первом этапе мы нашли длину ключевого слова . Рассмотрим теперь вопрос о нахождении самого ключевого слова. Для его нахождения можно исполь­зовать так называемый взаимный индекс совпадения.

Пусть х=(х₁,...,х_m),у=(у₁,...,y_l) – две строки букв алфавита А. Взаимным индексом совпадения в х и у, обозначаемым МI_c(х,у), называется вероятность того, что случайно выбранная буква из х совпадает со случайно выбранной буквой из у.

Пусть f_i – число вхождений буквы а_i в х, g_i – число вхождений буквы а_i в y, iZ_n.

Теорема. Взаимный индекс совпадения в х и у вычисля­ется по формуле

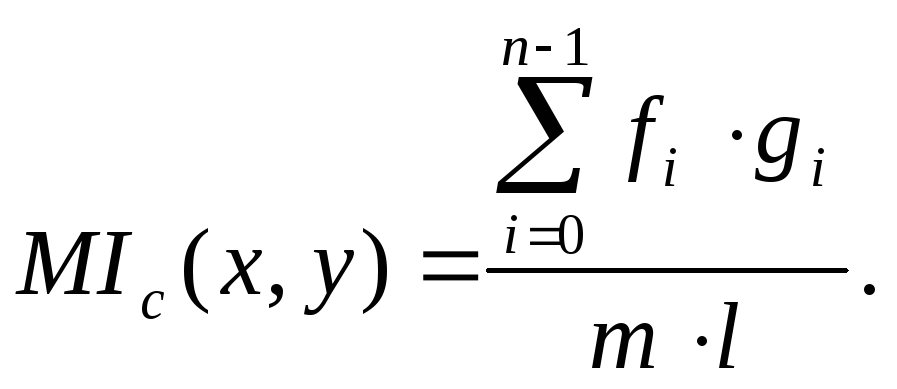
(19)

Пусть k=(k₁,...,k_ ) – истинное ключевое слово. Попытаемся оценить индексы М1_c(Y_i, Y_j).

Для этого напомним, что Y_s является результатом за­шифрования фрагмента открытого текста простой заменой букв алфавита (подстановкой) со сдвигом s. На основании этого получаем:

(20)

Заметим, что сумма в правой части последнего равенства зависит только от разности (s_i -s_j)mod n, которую назовем относительным сдвигом Y_i и Y_j, поэтому Y_i и Y_j с относительными сдвигами s и п – s имеют одинаковые взаимные индексы совпадения. Приведем таблицу значений сумм (20) для английского языка:

Таблица 7. Взаимный индекс совпадения при сдвиге s

Сдвиг s	0	1	2	3	4	5	6	7	8	9	10	11	12	13
MIc(x,y)	0,066	0,039	0,032	0,034	0,044	0,033	0,036	0,039	0,034	0,034	0,038	0,045	0,039	0,043

Аналогичные таблицы можно получить и для других языков.

Обратим внимание на то, что ненулевые "сдвиги" дают взаимные индексы совпадения, изменяющиеся в пределах от 0,032 до 0,045, в то время как при нулевом сдвиге индекс М1_с(х,у) близок к 0,066. Это наблюдение позволяет опреде­лить величины относительных сдвигов s_i – s_j столбцов Y_i и Y_j .

Используя изложенный метод, мы сможем связать систе­мой уравнений относительные сдвиги различных пар столб­цов Y_i и Y_j .В результате останется 26 вариантов для клю­чевого слова, из которых можно выбрать наиболее предпочтительный вариант (если ключевое слово является осмысленным).

Следует отметить, что предложенный метод будет эф­фективным для не слишком больших значений . Это объясняется тем, что для хороших приближений индексов совпа­дения требуются тексты достаточно большой длины.

Контрольные вопросы

1. Приведите пример шифра перестановки, который может рассматриваться и как блочный шифр замены.

2. Как определить по криптограмме, полученной с помощью шифра вертикальной перестановки, число коротких столб­цов заполненного открытым текстом основного прямо­угольника?

3. Какие свойства открытого текста используются при вскры­тии шифра вертикальной перестановки?

4. Каким образом можно использовать вероятные слова для вскрытия ряда криптограмм, полученных на одном ключе шифра перестановки?

5. С какими примерами шифров замены и перестановки Вы познакомились в историческом обзоре?

6. Существуют ли шифры, не являющиеся ни шифрами за­мены, ни шифрами перестановки?

7. Приведите пример шифра многозначной замены.

8. Может ли блочный шифр быть шифром разнозначной за­мены?

9. Может ли шифр простой замены быть равнозначным, разнозначным, блочным шифром?

10. В каком случае шифр гаммирования является одноалфа­витным шифром?

11. Каково максимальное число простых замен, из которых может состоять многоалфавитный шифр?

12. Можно ли рассматривать множество возможных откры­тых и шифрованных текстов как множество шифровеличин и шифрообозначений шифра замены?

13. Какие шифры называются шифрами простой замены?

14. Что является ключом шифра простой замены? Каково макси­мально возможное число ключей шифра простой замены?

15. Что более целесообразно для надежной защиты информации:

архивация открытого текста с последующим шифрованием или шифрование открытого текста с последующей архиваци­ей?

16. Имеет ли шифр Плейфера эквивалентные ключи, то есть такие ключи, на которых любые открытые тексты шифруются оди­наково? Сколько различных неэквивалентных ключей имеет шифр Плейфера?

17. Предположим, что матричный шифр Хилла используется для зашифрования открытого текста, представленного в виде дво­ичной последовательности. Сколько ключей имеет такой шифр?

18. В чем слабость шифра гаммирования с неравновероятной гаммой?

19. Является ли надежным шифрование литературного текста с помощью модульного гаммирования, использующего гамму, два знака которой имеют суммарную вероятность, совпадающую с суммарной вероятностью остальных зна­ков? Почему?

20. Почему наложение на открытый текст гаммы, представ­ляющей собой периодическую последовательность не­большого периода, не дает надежной защиты?

21. Почему недопустимо использовать дважды одну и ту же гамму (даже случайную и равновероятную!) для зашиф­рования разных открытых текстов?

22. Почему в качестве гаммы нецелесообразно использовать текст художественного произведения? Можете ли Вы предложить метод вскрытия такого шифра?

23. Можно ли по шифртексту получить приближения для вероятностей знаков гаммы?

24. Назовите основные этапы работы по вскрытию шифра Виженера.

25. Каким образом рассчитывается индекс совпадения для реального языка?

26. Из каких простых замен «состоит» шифр гаммирования (как многоалфавитный шифр)?