
- •Sommaire
- •3.3 Applications du calcul intégral……………........................................50
- •3.4 Révision...............................................................................................52
- •1. DÉrivabilitÉ
- •1 .1 Fonctions exponentielles
- •Etude de la fonction
- •Applications
- •1) Résoudre l’équation
- •2) Résoudre l’équation
- •3) Résoudre l’inéquation
- •Exercices
- •1.2 Fonctions logarithmes
- •Propriétés algébriques
- •Applications
- •3) Résoudre l’inéquation
- •Exercices
- •1.3 Dérivée d’une fonction
- •Tableau récapitulatif des dérivées usuelles
- •Opérations sur les fonctions dérivables
- •Exercices
- •1.4 Applications de la dérivabilité
- •La tangente à une courbe (касательная к кривой)
- •Étudier les variations et les extremums d’une fonction
- •Problèmes d’optimisation
- •Tangente à une courbe
- •Exercices
- •1.5 Révision
- •2. Des objets de l’espace : les solides
- •2. 1 Prismes
- •Propriétés des parallélépipèdes droits
- •Formules
- •Exercices
- •2. 2 Pyramides
- •Formules
- •Exercices
- •2. 3 Solides de révolution
- •5) La section du cylindre par le plan p
- •6) Section d’un cylindre par un plan parallèle а l’axe
- •Formules
- •3) Section du cône par un plan parallèle à la base
- •Formules
- •Formules
- •Exercices
- •2.4 Révision
- •3. Calcul IntÉgral
- •3. 1 Primitives
- •Primitives usuelles
- •Primitive d'une fonction définie par une "condition initiale"
- •Cas des fonctions composées
- •Exercices
- •3. 2 Définition et propriétés des intégrales
- •3) Relation de Chasles
- •Exercices
- •3.3 Applications du calcul intégral
- •1) Aire sous la courbe
- •2) Aire entre les courbes
- •3) Calcul de volume
- •Exercices
- •3.4 Révision
- •4. Organisation et gestion de donnÉes
- •4. 1 Ensembles
- •Opérations ensemblistes
- •Désignation des ensembles
- •Exercices
- •4. 2 Éléments de combinatoire
- •Principe de multiplication
- •Principe d’addition
- •Exercices
- •4.3 Probabilités
- •Propriétés
- •Exercices
- •4. 4 Statistiques
- •Caractéristiques d’une série statistique
- •Représentations graphiques
- •Exercices
- •266) Au poste de péage, on compte le nombre de voitures se présentant sur une période de 5mn. Sur 100 observations de 5mn, on obtient les résultats suivants :
- •4.5 Révision
1.5 Révision
57) Pour chacune des fonctions définies ci-dessous, préciser son ensemble de définition
|
a) f(x) = |
b) g(x) = (ln x)² |
c) h(x) = ln(3x – 5) |
|
d) i(x) = ln(x² + x + 1) |
e) k(x) = ln |
f) m(x) = ln (ln x) |
58)
Simplifier
les écritures suivantes : a)![]()
b)![]() c)
c)![]()
d)
![]() e)
e)
![]() f)
f)
![]()
59) Résoudre les équations suivantes :
a)![]() b)
b)![]() c)
c)![]() d)
d)
![]()
e)
![]() f)
f)![]() g)
g)
![]()
h)
![]() i)
i)
![]() j)
j)
![]()
60) Résoudre les inéquations suivantes :
a)![]() b)
b)![]() c)
c)![]() d)
d)![]() e)
e)![]()
61) Résoudre les équations suivantes :
a)
![]() b)
b)
![]() c)
c)
![]() d)
d)
![]() e)
e)
![]()
f)
![]() g)
g)
![]() h)
h)
![]() i)
i)
![]()
62) Simplifier les expressions suivantes :
a)
![]() b)
b)
![]() c)
c)
![]()
63) Résoudre les inéquations suivantes :
a)
![]() b)
b)
![]() c)
c)
![]() d)
d)
![]()
e)
![]() f)
f)
![]() g)
g)
![]()
64) Pour chacune des fonctions suivantes, donner le domaine de définition de la fonction, calculer la dérivée et donner le domaine de définition de la dérivée.
a)
![]() b)
b)
![]() c)
c)
![]() d)
d)
![]() e)
e)
![]() f)
f)
![]() g)
g)
![]() h)
h)
![]()
i)
![]() j)
j)
![]() k)
k)
![]()
65) Calculer le nombre dérivé des fonctions suivantes
a)![]() en
en
![]() b)
b)![]() en
x = 3
en
x = 3
c)
![]() en
x = 1 d)
en
x = 1 d)
![]() en x
= 1
en x
= 1
66) Trouver les intervalles de croissance et de décroissance ainsi que les extremums relatifs de chacune des fonctions associées aux équations suivantes.
a)
![]() b)
b)
![]() c)
c)
![]() d)
d)
![]()
e)
![]() f)
f)
![]() g)
g)
![]() h)
h)![]()
67)
La fonction L(x) =
![]() représente la production laitière en litres d’une vache. Dans
cette équation, x est le niveau hormonal en cm3
injecté par jour а
cette vache (0 ≤ x ≤ 10).
représente la production laitière en litres d’une vache. Dans
cette équation, x est le niveau hormonal en cm3
injecté par jour а
cette vache (0 ≤ x ≤ 10).
a) Déterminer le niveau hormonal qui maximise la production laitière.
b) Trouver cette production maximale.
68)
On considère les fonctions f et g définir par
![]() et
et
![]() Déterminer
le coefficient directeur de la tangente à la représentation
graphique de chacune de ces fonctions au point d’abscisse 4.
Déterminer
le coefficient directeur de la tangente à la représentation
graphique de chacune de ces fonctions au point d’abscisse 4.
69) Dons chacun des cas suivants, déterminer une équation de la tangente à la courbe représentative de f au point d’abscisse a donné.
a)
![]() b)
b)
![]() c)
c)
![]()
d)![]() e)
e)
![]() f)
f)
![]()
2. Des objets de l’espace : les solides
2. 1 Prismes
Mots à retenir
un polygone (многоугольник) une face (грань) une arête (ребро)
latéral (боковой) superposable (совпадающий)
un prisme à base triangulaire (треугольная призма)
un patron (развёртка) une section (сечение) une hauteur (высота)
l’aire latérale (площадь боковой поверхности)
l’aire totale (площадь полной поверхности)
l e
volume (объём)
e
volume (объём)
Définitions
1) Un prisme est un objet de l'espace qui a :
-
deux faces de base parallèles. Les bases sont des polygones.
-
toutes ses arêtes latérales parallèles.
2) La hauteur d'un prisme est la distance séparant les deux plans des bases.
3) Un patron d'un prisme est un dessin sur un plan qui représente le prisme "déplié". Nous y voyons donc toutes ses faces et ses bases en vraie grandeur.
Propriétés
1) Les deux bases d'un prisme sont des polygones (réguliers ou non). Ces deux polygones sont superposables.
2) Les faces latérales sont des parallélogrammes.
3) Les arêtes latérales ont toutes la même longueur.
Définitions
3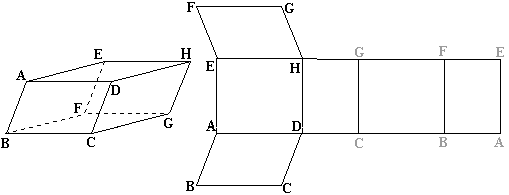 )
On
appelle prisme
droit
un prisme dont les arêtes
latérales
sont perpendiculaires
aux plans
des bases (les faces latérales de ces prismes sont donc des
rectangles).
)
On
appelle prisme
droit
un prisme dont les arêtes
latérales
sont perpendiculaires
aux plans
des bases (les faces latérales de ces prismes sont donc des
rectangles).
4) On appelle parallélépipède un prisme dont la base est un parallélogramme.
5) On appelle parallélépipède droit un prisme droit dont la base est un parallélogramme.
6 )
On
appelle parallélépipède
rectangle (le
pavé)
un prisme droit dont les bases
sont des rectangles.
)
On
appelle parallélépipède
rectangle (le
pavé)
un prisme droit dont les bases
sont des rectangles.
7 )
Le
cube n’est
qu’un
parallélépipède
particulier : les six faces
sont des carrés
identiques.
)
Le
cube n’est
qu’un
parallélépipède
particulier : les six faces
sont des carrés
identiques.
