
- •Sommaire
- •3.3 Applications du calcul intégral……………........................................50
- •3.4 Révision...............................................................................................52
- •1. DÉrivabilitÉ
- •1 .1 Fonctions exponentielles
- •Etude de la fonction
- •Applications
- •1) Résoudre l’équation
- •2) Résoudre l’équation
- •3) Résoudre l’inéquation
- •Exercices
- •1.2 Fonctions logarithmes
- •Propriétés algébriques
- •Applications
- •3) Résoudre l’inéquation
- •Exercices
- •1.3 Dérivée d’une fonction
- •Tableau récapitulatif des dérivées usuelles
- •Opérations sur les fonctions dérivables
- •Exercices
- •1.4 Applications de la dérivabilité
- •La tangente à une courbe (касательная к кривой)
- •Étudier les variations et les extremums d’une fonction
- •Problèmes d’optimisation
- •Tangente à une courbe
- •Exercices
- •1.5 Révision
- •2. Des objets de l’espace : les solides
- •2. 1 Prismes
- •Propriétés des parallélépipèdes droits
- •Formules
- •Exercices
- •2. 2 Pyramides
- •Formules
- •Exercices
- •2. 3 Solides de révolution
- •5) La section du cylindre par le plan p
- •6) Section d’un cylindre par un plan parallèle а l’axe
- •Formules
- •3) Section du cône par un plan parallèle à la base
- •Formules
- •Formules
- •Exercices
- •2.4 Révision
- •3. Calcul IntÉgral
- •3. 1 Primitives
- •Primitives usuelles
- •Primitive d'une fonction définie par une "condition initiale"
- •Cas des fonctions composées
- •Exercices
- •3. 2 Définition et propriétés des intégrales
- •3) Relation de Chasles
- •Exercices
- •3.3 Applications du calcul intégral
- •1) Aire sous la courbe
- •2) Aire entre les courbes
- •3) Calcul de volume
- •Exercices
- •3.4 Révision
- •4. Organisation et gestion de donnÉes
- •4. 1 Ensembles
- •Opérations ensemblistes
- •Désignation des ensembles
- •Exercices
- •4. 2 Éléments de combinatoire
- •Principe de multiplication
- •Principe d’addition
- •Exercices
- •4.3 Probabilités
- •Propriétés
- •Exercices
- •4. 4 Statistiques
- •Caractéristiques d’une série statistique
- •Représentations graphiques
- •Exercices
- •266) Au poste de péage, on compte le nombre de voitures se présentant sur une période de 5mn. Sur 100 observations de 5mn, on obtient les résultats suivants :
- •4.5 Révision
Étudier les variations et les extremums d’une fonction
Intuitivement lorsqu’on se déplace de gauche vers la droite sur l’axe des x et que le graphique d’une fonction monte, on dit que la fonction est croissante; lorsque le graphique descend, la fonction est dite décroissante.
Méthode 1 Pour trouver le sens de variation d’une fonction, on cherche le signe de sa dérivée.
Soit ƒ une fonction dérivable sur l’intervalle I. Si pour chaque x dans l’intervalle I
-
ƒ ’(x) > 0 alors ƒ est croissante sur I,
-
ƒ ’(x) < 0 alors ƒ est décroissante sur I.
Exemple Trouver
les intervalles de croissance et de décroissance de la fonction
![]()
Rédaction :
a)
![]() b)
b)
![]()
Pour déterminer où sur l’ensemble définition de la fonction, la dérivée est positive et où, elle est négative, on construit le tableau des signes de ƒ ’. Pour cela on doit d’abord déterminer les endroits où la dérivée peut changer de signe. Il peut se produire un changement de signe seulement aux endroits où la dérivée passe par zéro ou n’existe pas. On doit d’abord trouver ces valeurs :
![]() Donc les
nombres critiques sont 3 et 1.
Donc les
nombres critiques sont 3 et 1.
c) A l’aide des valeurs trouvées, on construit le tableau des signes de la dérivée.
|
x |
|
|
signe
de
|
+ 0 - 0 + |
|
variations
de
|
|
Réponse :
la fonction est décroissante sur ]1, 3[ , croissante sur
![]() .
.
Méthode 2 Pour obtenir les extremums relatifs d’une fonction, il suffit de trouver
les nombres critiques de la fonction puis de déterminer ensuite la nature de chaque nombre critique.
Soit ƒ une
fonction dérivable sur l’intervalle I et x0
un réel de I. Si
![]() s’annule
en x0
en changeant de signe,
alors
s’annule
en x0
en changeant de signe,
alors
![]() admet
un
extremum
en x0.
admet
un
extremum
en x0.
-
 admet
un
maximum
en x0
admet
un
maximum
en x0
|
x |
x0 |
|
signe
de
|
+ 0 - |
|
variations
de
|
|
-
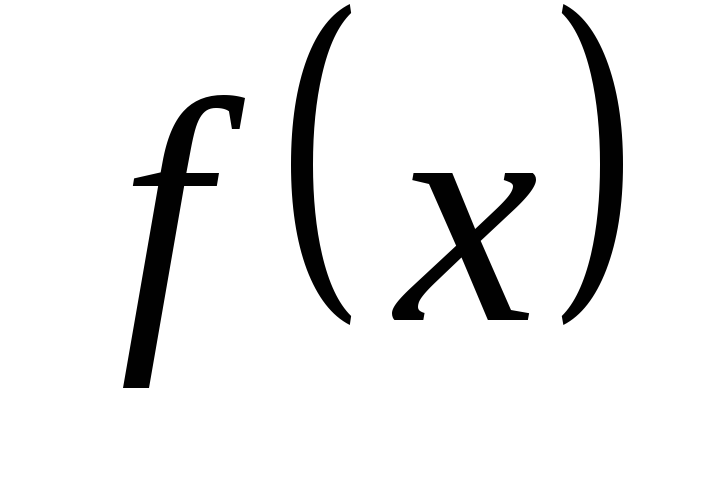 admet
un
minimum
en x0
admet
un
minimum
en x0
|
x |
x0 |
|
signe
de
|
- 0 + |
|
variations
de
|
|
Exemple :
Trouver
les intervalles de croissance, de décroissance ainsi que les
extremums de la fonction![]()
Rédaction :
a)
![]() b)
b)
![]() est
continue sur
est
continue sur![]()
c)
![]() Les
nombres critiques sont 1 et -1 car 0 ne
fait pas partie de l’ensemble
définition de la fonction.
Les
nombres critiques sont 1 et -1 car 0 ne
fait pas partie de l’ensemble
définition de la fonction.
c) Tableau des signes de la dérivée :
|
x |
|
|
signe
de
|
+ 0 - | - 0 + |
|
variations
de
|
max | 2 |
Réponse :
la fonction est décroissante sur![]() ,
croissante sur
,
croissante sur
![]() ,
,
![]()
![]()
Méthode 3 Un plan d’étude d’une fonction
L’étude complète d’une fonction obéit à la procédure suivante :
1) préciser d’abord l’ensemble de définition ;
2) examiner si la fonction est paire ou impaire et en tirer les conséquences graphiques ;
3) déterminer les limites nécessaires ;
4) calculer la dérivée, étudier son signe, en déduire les variations de la fonction, dresser un tableau qui résume tous ces résultats ;
5) dessiner une représentation graphique aussi précise que possible, tenant compte de toutes les informations précédentes.







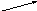



 -2
min
-2
min