Applications

1) Résoudre l’équation ln (2x-3) = ln (6 -x) après avoir déterminé le domaine de définition.

Rédaction : l’équation est définie si . Donc, le domaine de définition de l’équation est D = On sait que si ln a = ln b alors a = b. Ainsi pour l’équation équivaut à

Comme alors cette solution convient. Réponse : x = 3.

2) Résoudre l’équation ln (x-1) + ln (x-3) = ln 3

Rédaction : l’équation est définie si 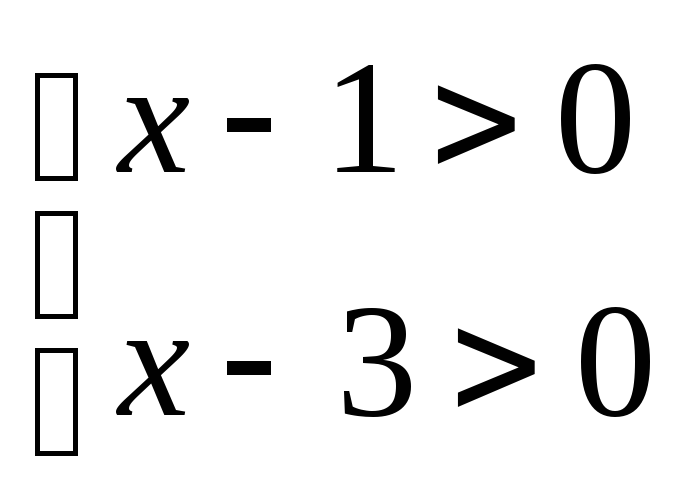. Le domaine de définition de l’équation est D = . L’équation peut encore s’écrire : Ainsi pour l’équation équivaut à

Ce qui donne x = 0 ou x = 4. Comme et on obtient que 4 est la racine de l’équation. Réponse : x = 4.

3) Résoudre l’inéquation

Rédaction : Le domaine de définition de l’équation est D = . L’inéquation peut encore s’écrire : soit car la fonction f(x) = ln x est strictement croissante. D’où Faisons un tableau de signes.

x	0 4
x	- 0 + +
x – 4	- - 0 +
	+ 0 - 0 +

Il nous faut donc : et On obtient Réponse :

Définitions

4) Soit un nombre réel a différent de 1 et strictement positif. La fonction logarithme de base a est notée f (x) = log_a x. Elle est définie par

5) La fonction logarithme de base dix (logarithme décimal) est notée f(x)= log x avec log 10 = 1 et log = p.

Elle possède les mêmes propriétés algébriques que la fonction logarithme népérien.

Exercices

14) Trouver les valeurs de x pour lesquelles les fonctions ci-dessous sont définies.

a) b) c) d)

e) f) g) h)

15) Simplifier les expressions suivantes :

16) Résoudre les équations suivantes :

a) b) c) d) e) f)

g) h) i)

j) k) l)

17) Résoudre les inéquations suivantes :

a) b) c) d) e) f) g)

18) Justifier ou infirmer les égalités suivantes :

a) ln 72 = 3 ln 2 + 2 ln 3	b) ln = 4 ln 2 – 3 ln 7
c) ln 625 = 5 ln 4	d) ln 0,8 = 2 ln 2 – ln 5
e) ln = - (ln 2 + ln 3)

19) Écrire plus simplement :

a) b) c) d)

e) f) g)

20) Trouver l’ensemble de définition des fonctions suivantes :

a) b) c) d)

e) f) g) h)

21) Résoudre les équations suivantes :

a) ln(2x – 3) = ln(x + 5) b) 2 ln(x – 3) = ln 4 c) ln(x) = 6 d) ln =

e) ln(3x) = -1 f) ln() = 2 g) ln(x² – 2x – 3) = ln(x – 2) h) ln² x – 4 ln x – 5 = 0

i) ln (x-3) + ln (x- 1) = 3 ln 2 j) −2ln2 + ln ( −1 + x) = 0 k)

22) Résoudre les inéquations suivantes :

a) ln x + ln(x + 2)  ln(x² – 2x + 2) b) ln(x² + 2x + 2)  ln(3 – x) + ln(x + 1)

c) ln(35 – 8x)  3 ln 2 + ln(x²) d) e)

23) Déterminer le signe de l’expression définie sur ]0 ;+¥[  par  la formule A(x) = (x² – 4x – 5) ln x.

24) Exprimer sous forme d’un seul logarithme :

a) b) c)

25) Décomposer à l'aide des propriétés des logarithmes :

a) b) c)

26) Résoudre les équations suivantes :

a) b) c) d)

27) Résoudre les inéquations suivantes :

a) b) c)