
- •Sommaire
- •3.3 Applications du calcul intégral……………........................................50
- •3.4 Révision...............................................................................................52
- •1. DÉrivabilitÉ
- •1 .1 Fonctions exponentielles
- •Etude de la fonction
- •Applications
- •1) Résoudre l’équation
- •2) Résoudre l’équation
- •3) Résoudre l’inéquation
- •Exercices
- •1.2 Fonctions logarithmes
- •Propriétés algébriques
- •Applications
- •3) Résoudre l’inéquation
- •Exercices
- •1.3 Dérivée d’une fonction
- •Tableau récapitulatif des dérivées usuelles
- •Opérations sur les fonctions dérivables
- •Exercices
- •1.4 Applications de la dérivabilité
- •La tangente à une courbe (касательная к кривой)
- •Étudier les variations et les extremums d’une fonction
- •Problèmes d’optimisation
- •Tangente à une courbe
- •Exercices
- •1.5 Révision
- •2. Des objets de l’espace : les solides
- •2. 1 Prismes
- •Propriétés des parallélépipèdes droits
- •Formules
- •Exercices
- •2. 2 Pyramides
- •Formules
- •Exercices
- •2. 3 Solides de révolution
- •5) La section du cylindre par le plan p
- •6) Section d’un cylindre par un plan parallèle а l’axe
- •Formules
- •3) Section du cône par un plan parallèle à la base
- •Formules
- •Formules
- •Exercices
- •2.4 Révision
- •3. Calcul IntÉgral
- •3. 1 Primitives
- •Primitives usuelles
- •Primitive d'une fonction définie par une "condition initiale"
- •Cas des fonctions composées
- •Exercices
- •3. 2 Définition et propriétés des intégrales
- •3) Relation de Chasles
- •Exercices
- •3.3 Applications du calcul intégral
- •1) Aire sous la courbe
- •2) Aire entre les courbes
- •3) Calcul de volume
- •Exercices
- •3.4 Révision
- •4. Organisation et gestion de donnÉes
- •4. 1 Ensembles
- •Opérations ensemblistes
- •Désignation des ensembles
- •Exercices
- •4. 2 Éléments de combinatoire
- •Principe de multiplication
- •Principe d’addition
- •Exercices
- •4.3 Probabilités
- •Propriétés
- •Exercices
- •4. 4 Statistiques
- •Caractéristiques d’une série statistique
- •Représentations graphiques
- •Exercices
- •266) Au poste de péage, on compte le nombre de voitures se présentant sur une période de 5mn. Sur 100 observations de 5mn, on obtient les résultats suivants :
- •4.5 Révision
3) Relation de Chasles
Remarque La relation de Chasles permet d'étendre la définition de l'intégrale au cas où la fonction f n'est continue que par morceaux sur l'intervalle d'intégration. On intègre séparément chacun des morceaux et on ajoute ensuite les intégrales obtenues.
E xemple
Considérons la fonction f qui vaut x si
xemple
Considérons la fonction f qui vaut x si
![]() et
et
![]() si
si
![]() .
Son
intégrale sur l'intervalle
.
Son
intégrale sur l'intervalle
![]() vaut :
vaut :
![]()
4)
![]() avec
k réel.
On
l'utilisera souvent, soit pour mettre en facteur une constante devant
l'intégrale.
avec
k réel.
On
l'utilisera souvent, soit pour mettre en facteur une constante devant
l'intégrale.
5)
Linéarité
de l'intégrale
![]()
On l'utilisera souvent pour séparer le calcul en deux intégrales plus simples.
Exemple

Exercices
163) Calculer l'intégrale proposée :
a)![]() b)
b)![]() c)
c)
![]() d)
d)
 e)
e)
![]() f)
f)

g)
![]() h)
h)
![]() i)
i)![]() j)
j)
![]() k)
k)
![]()
164) Calculer chacune des intégrales suivantes. Faire apparaître sur un dessine les aires représentées par chacune des intégrales.
a)
![]() b)
b)
![]() c)
c)
![]() d)
d)
![]() e)
e)
![]()
165) Calculer chacune des intégrales suivantes :
a)
![]() b)
b)
![]() c)
c)
![]() d)
d)
![]()
166) Calculer chacune des intégrales suivantes :
a)
![]() b)
b)
![]() c)
c)
 d)
d)
![]() e)
e)
![]()
167) Calculer chacune des intégrales suivantes :
a)
![]() b)
b)
![]() c)
c)
![]() d)
d)
![]() e)
e)
![]() f)
f)
![]() g)
g)
![]() h)
h)
![]() i)
i)
![]() j)
j)
![]() k)
k)
![]()
168) Calculer l'intégrale proposée :
a)
![]() b)
b)
![]() c)
c)
![]() d)
d)
![]() e)
e)

169) Calculer chacune des intégrales suivantes :
a)
 b)
b)
 c)
c)
 d)
d)

e)
![]() f)
f)
![]() g)
g)
![]() h)
h)
![]()
170) Calculer chacune des intégrales suivantes :
a)
 b)
b)
![]() c)
c)

171) Calculer chacune des intégrales suivantes :
a)
![]() b)
b)
![]() c)
c)
![]()
3.3 Applications du calcul intégral
Mots à retenir
engendrer (образовывать, рождать, порождать, производить)
1) Aire sous la courbe
S oient
a et b deux réels tels que a ≤ b, f une fonction f définie et
continue sur l’intervalle
oient
a et b deux réels tels que a ≤ b, f une fonction f définie et
continue sur l’intervalle
[a ; b], et C sa courbe représentative dans un repère orthogonal. Si pour tout x de [a ; b],
f(x) ≥ 0,
alors
![]() est l’aire, en unités d’aire, du domaine compris entre la courbe
C, l’axe des abscisses et les droites d’équations
est l’aire, en unités d’aire, du domaine compris entre la courbe
C, l’axe des abscisses et les droites d’équations
x = a et x = b.
2) Aire entre les courbes
S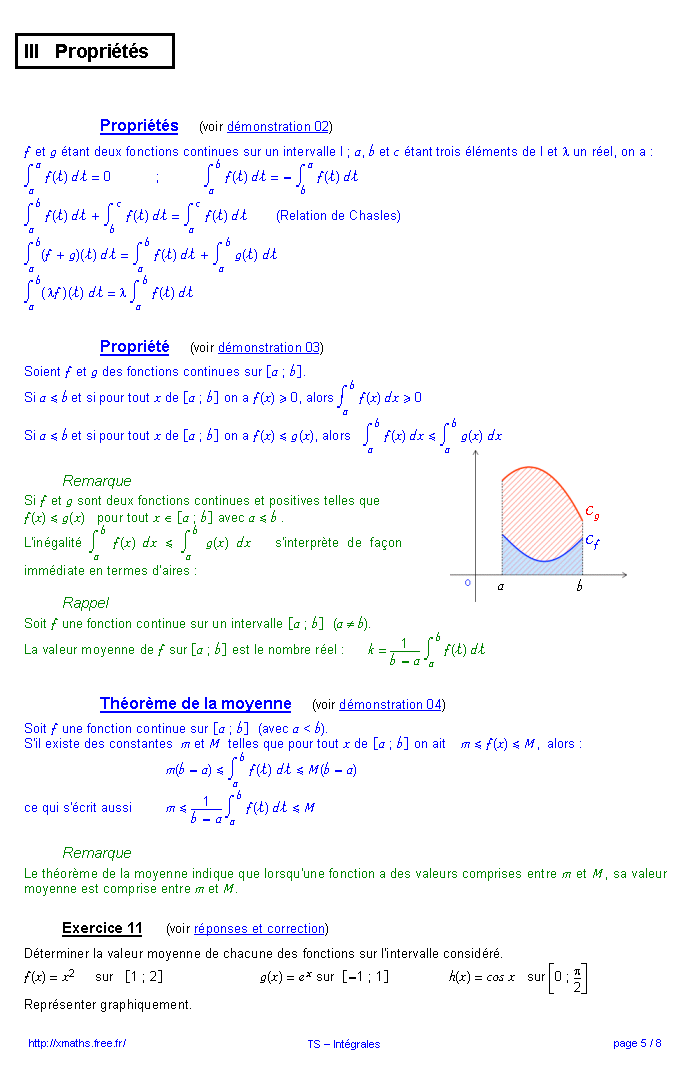 oient
f et g deux fonctions continues sur [a ; b] telles que : pour
tout x de [a ; b], f(x) ≤ g(x). Dans un repère orthogonal,
l’aire de la surface limitée par les représentations graphiques
de f et g et les droites d’équations x = a et x = b est :
oient
f et g deux fonctions continues sur [a ; b] telles que : pour
tout x de [a ; b], f(x) ≤ g(x). Dans un repère orthogonal,
l’aire de la surface limitée par les représentations graphiques
de f et g et les droites d’équations x = a et x = b est :
![]() en
unités d’aires.
en
unités d’aires.
Exemple On cherche l’aire comprise entre les paraboles y = x2 –2x+2 et y = - x2 + 6
Rédaction : on cherche les points d’intersection entre ces paraboles :
x2 – 2x + 2 = - x2 + 6 soit 2x2 –2x –4 = 0 ; les solutions de cette équation sont
x = -1 ou x
= 2. On cherche l’aire comprise entre les paraboles.
![]()
Réponse : A = 9
3) Calcul de volume
a) Pour
un volume V de hauteur H dont la section avec un plan à la hauteur h
a pour l’aire S(h) on a
![]() unités
de volume.
unités
de volume.
b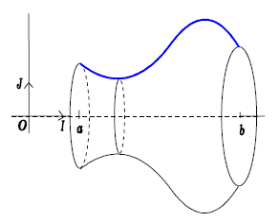 )
Le volume V du solide de révolution
)
Le volume V du solide de révolution
engendré par rotation de la région délimitée
par le graphe Cf et les droites x = a et x = b
autour de l’axe des x est donnée par
la formule
suivante :
![]()
Exercices
1 72)
Calculer l’aire de la surface limitée par les représentations
graphiques de
72)
Calculer l’aire de la surface limitée par les représentations
graphiques de
![]() Faire
la figure.
Faire
la figure.
173)
Archimède
a démontré que l’aire d’un secteur compris entre une droite et
une parabole était égal à quatre tiers de l’aire du triangle de
même base et même hauteur que ce secteur. On a représenté
ci-contre la fonction f définie sur R par
![]() .
.
• Calculer l’aire A0 du triangle OAB. En déduire l’aire A du secteur colorié.
• Trouver une primitive F de f. Comparer F(6) − F(0) et A.
174)
On donne les fonctions f
et
g.
Calculez l'aire du domaine borné
délimité
par les deux fonctions : a)![]()
b)
![]() c)
c)
![]()
175) Calculez l'aire du domaine compris entre les courbes des fonctions f et g et les droites verticales x = a et x = b.
a)
![]() b)
b)
![]()
176)
Calculez
l'aire du domaine compris entre les courbes y
=
x,
![]() et les droites horizontales
y
=
1 et y
=
2.
et les droites horizontales
y
=
1 et y
=
2.
177) Calculez le volume des solides générés par la révolution autour de l'axe (OX) des courbes suivantes:
a)
![]() b)
b)
![]() c)
c)
![]()
d)
![]() e)
e)
![]() f)
f)
![]()
178) Donnez la formule permettant de trouver le volume engendré par une révolution autour de l'axe (OY), puis calculez le volume du solide généré par la révolution autour de l'axe (OY) de la courbe : y = x3, 0 y 1.
179)
Calculer
l'aire de la figure limitée par la courbe![]() ,
la droite y = 8 et l'axe des ordonnées.
,
la droite y = 8 et l'axe des ordonnées.
180)
Calculer
l'aire de la figure comprise entre les paraboles![]() ,
,
![]() et
la droite y = 2x.
et
la droite y = 2x.
181)
Calculer
l'aire de la figure comprise entre la parabole
![]() et
la droite y = -x.
et
la droite y = -x.
182)
Calculer
l'aire du segment de parabole
![]() défini
par la droite y = 3-2x.
défini
par la droite y = 3-2x.
183)
Calculer l'aire de la figure limitée par la courbe y =sin x, l'axe
des abscisses et les droites
![]() et
et
![]()
184)
Calculer l'aire de la figure limitée par la courbe![]() ,
l'axe des abscisses et les droites x = 0 et x = π.
,
l'axe des abscisses et les droites x = 0 et x = π.
185) Calculer la surface latérale d'un cône de hauteur h et de rayon de base R.
186) Calculer le volume d’une sphère de rayon R.
187)
Dans
un
plan rapporté à un repère orthonormal d’unité 1cm, on considère
la courbe représentant la fonction sinus sur
![]() Calculer
le volume que l’on obtient par rotation de cette courbe autour de
l’axe (OX).
Calculer
le volume que l’on obtient par rotation de cette courbe autour de
l’axe (OX).
188)
Dans l'espace muni du repère orthonormé soient S la surface plane
située dans le plan z = 0 et délimité par les 2 courbes
d'équations respectives
![]() et
et
![]() .
D le solide engendré par la rotation de S autour de l'axe (OX). a)
Faire un croquis de S. b) Calculer l'aire de S. c) Calculer le volume
de D.
.
D le solide engendré par la rotation de S autour de l'axe (OX). a)
Faire un croquis de S. b) Calculer l'aire de S. c) Calculer le volume
de D.
