§ 5. Комплексный чертеж из трех и более видов и прямоугольная система координат в пространстве

1. Профильная плоскость проекций. Как было показано, комплексный чертеж, состоящий из видов спереди и сверху^, является обратимым, т. е. по этому чертежу можно реконструировать оригинал. Однако реконструкция оригинала, у которого имеются профильные элементы и, в частности, профильные прямые или плоскости, становится проще, когда помимо видов спереди и сверху имеется еще и вид на третьей плоскости. В качестве такой плоскости проекций применяется плоскость, перпендикулярная к обеим основным плоскостям 1 и 2, называемая профильной плоскостью проекций^, ее обозначают 3, а изображение на ней называют видом слева.

Три плоскости проекций 1, 2 и 3 образуют систему трех взаимно перпендикулярных плоскостей (рис. 18а).

а б

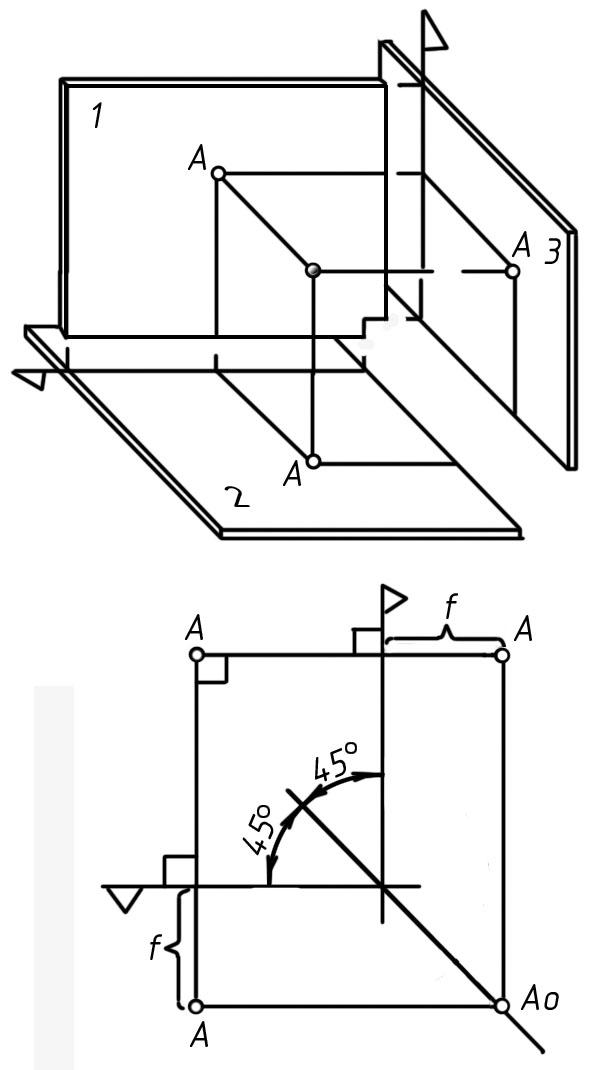
Рис. 18

2. Трехкартинный комплексный чертеж. Рассмотрим образование такого чертежа некоторой точки А при нефиксированных плоскостях проекций. Спроецировав ортогонально на плоскости проекций 1, 2 и 3 данную точку А, получим в дополнение к ее видам спереди и сверху вид слева (рис. 18а). Расстояния точки А от фиксированных горизонтальной и фронтальной плоскостей проекций ранее были названы соответственно высотой h и глубиной f точки А; расстояние же точки А от фиксированной профильной плоскости проекций называется широтой р точки А.

Если теперь совместить плоскости проекций 1, 2 и 3 с плоскостью чертежа так, чтобы проекции проецирующей плоскости на плоскостях 1 и 2 оказались на одной вертикальной прямой (вертикальной линии связи), а проекции проецирующей плоскости на плоскостях 1 и 3 – на одной горизонтальной прямой (горизонтальной линии связи), то получим комплексный чертеж точки А в трех видах (рис. 18б). Если зафиксировать плоскость проекции 1 и принять ее за базовую плоскость, то глубина f точки А может быть измерена на видах сверху и слева от баз отсчета глубин, отмеченных знаком треугольника. Следовательно, для построения точки А на виде слева, заданной на видах спереди и сверху, нужно провести через точку А на виде спереди горизонтальную линию связи, на которой отложить от базы отсчета глубин величину, предварительно измеренную на виде сверху от той же базы отсчета.

При построении точки на виде слева можно использовать постоянную прямую преломления, обеспечивающую сохранение глубины точки (см. рис. 18б). Постоянная прямая преломления, являясь биссектрисой прямого угла между базами, будет наклонена к вертикальным и горизонтальным линиям связи под одним и тем же углом 45. Итак, три вида какой-либо точки А являются вершинами прямоугольника, четвертой вершиной которого является точка А₀, принадлежащая постоянной прямой преломления. При этом виды спереди и сверху связаны вертикальной линией связи, виды спереди и слева – горизонтальной линией связи и виды сверху и слева – ломаной горизонтально-вертикальной линией связи.

3. Пример, при решении которого будет использован вид слева. На профильной прямой р, заданной точками А и В, построить произвольную точку М (рис. 19).

Этот пример был уже решен (см. рис. 14) с помощью прямой преломления и ломаных линий связи. Теперь рассмотрим его решение с помощью вида слева прямой р. Для этого проведем постоянную прямую преломления под углом 45° к вертикальным линиям связи. Пользуясь прямой преломления, найдем на виде сверху точки А и В, определяющие прямую р.

Рис. 19

Если выбрать на виде слева точку М на прямой р произвольно, то эта точка легко определится и на видах спереди и сверху.

Сравнивая решение, приведенное ранее (см. рис. 14), с данным решением, нетрудно заметить, что последнее несколько сложнее первого, независимо от того, будет ли при последнем решении использована постоянная прямая преломления или оно будет выполнено с помощью измерения глубин точек. Единственным преимуществом последнего решения является его большая наглядность.

4. Дополнительные плоскости проекций. Часто при решении различных задач, а также при необходимости получения новых видов оригинала, помимо его шести видов на основных плоскостях проекций 1, 2, 3, 4, 5 и 6 приходится вводить новые дополнительные плоскости проекций 7, 8, ... . Эти плоскости располагают перпендикулярно любой из стандартных плоскостей проекций. Иначе говоря, новое направление проецирования должно быть параллельно одной из стандартных плоскостей проекций.

Так, например, введем дополнительную плоскость проекций 7, расположив ее перпендикулярно плоскости проекций 1 (рис. 20а). При этом новое направление проецирования будет параллельно плоскости 1, покажем его стрелкой (на рис. 20б эта стрелка изображена только на виде спереди). Спроецируем по этому направлению на плоскость 7 данную точку А.

При новом направлении проецирования сохраняется глубина f точки А относительно любой фронтальной плоскости Ф. Для упрощения изображения на рис. 20а за плоскость Ф принята фиксированная плоскость проекций 1. Глубина f точки А может быть измерена как на виде сверху, так и на дополнительном от баз отсчета глубин, отмеченных знаком треугольника.

а б

Рис. 20

Если теперь совместить плоскость проекций 7 с плоскостью чертежа так, чтобы проекции проецирующей плоскости точки А на плоскостях 2 и 7 оказались на одной прямой (наклонной линии связи, имеющей направление стрелки), то получим комплексный чертеж точки А в двух стандартных и одном дополнительном видах (рис. 20б).

Аналогичным образом можно ввести дополнительную плоскость проекций 7, перпендикулярную плоскости проекций 2 (рис. 21а). Новое направление проецирования, показанное стрелкой, будет параллельно плоскости проекций 2. При этом проецировании сохраняется высота h точки А относительно любой горизонтальной плоскости Г (на рис. 21а за плоскость Г принята фиксированная плоскость проекций 2). Высота h точки А может быть измерена на виде спереди или на дополнительном виде от баз отсчета высот, отмеченных знаком треугольника. В результате совмещения плоскости 7 с плоскостью чертежа получим комплексный чертеж точки А (рис. 21б) в двух стандартных и одном дополнительном видах.

Таким образом, при направлении проецирования, параллельном плоскости проекций 1, сохраняются глубины f относительно фронтальной плоскости Ф, а при направлении проецирования, параллельном плоскости проекций 2, сохраняются высоты h относительно горизонтальной плоскости Г.

а б

Рис. 21

Иначе говоря, для построения точки А на дополнительном виде по направлению проецирования, параллельному плоскости 1 (плоскости 2), нужно провести через точку А на виде спереди (виде сверху) линию связи в направлении, соответствующем направлению проецирования, и на этой линии связи следует отложить от базы отсчета дополнительного вида, отмеченного знаком треугольника, глубину f (высоту h) точки А, предварительно измеренную на виде сверху (спереди) от базы этого вида, отмеченной также знаком треугольника.

5. Пространственная система прямоугольных координат. Чтобы иметь возможность точной передачи и точного построения комплексных чертежей каких-либо оригиналов, необходимо уметь задавать положение точек на видах комплексного чертежа, при помощи чисел. Для этого, как известно, следует пользоваться координатным методом. Этот метод приходится также применять при построении аксонометрических чертежей (гл. VII).

Пространственная система прямоугольных координат Oxyz (рис. 22), употребляемая в координатном методе, состоит из трех взаимно перпендикулярных прямых х, у и z (осей координат), пересекающихся в одной точке О (начало координат), и трех взаимно перпендикулярных плоскостей хОу, xOz и yOz (плоскостей координат), попарно пересекающихся по соответствующим осям координат. Положительными направлениями координатных осей будем считать направления, указанные стрелками.

Три координатные плоскости делят пространство на восемь частей (октантов). Нумерация октантов показана на рис. 22. Каждому октанту соответствует своя система знаков направлений координатных осей. У первого октанта все три координатные оси имеют положительные направления.

Чтобы отнести данную точку А к выбранной системе коор- динат Oxyz, спроецируем ее ортогонально на координатную плоскость хОу. Получим проекцию точки А₂^, которую, в свою очередь, спроецируем ортогонально на координатную ось х в точку А_х. В результате этих двух проецирований получим пространственную ломаную линию OA_xA₂A (координатную ломаную), отрезки которой параллельны координатным осям и соответственно называются ОА_х – отрезком абсциссы, А_хА₂ – отрезком ординаты и А₂А – отрезком аппликаты.

2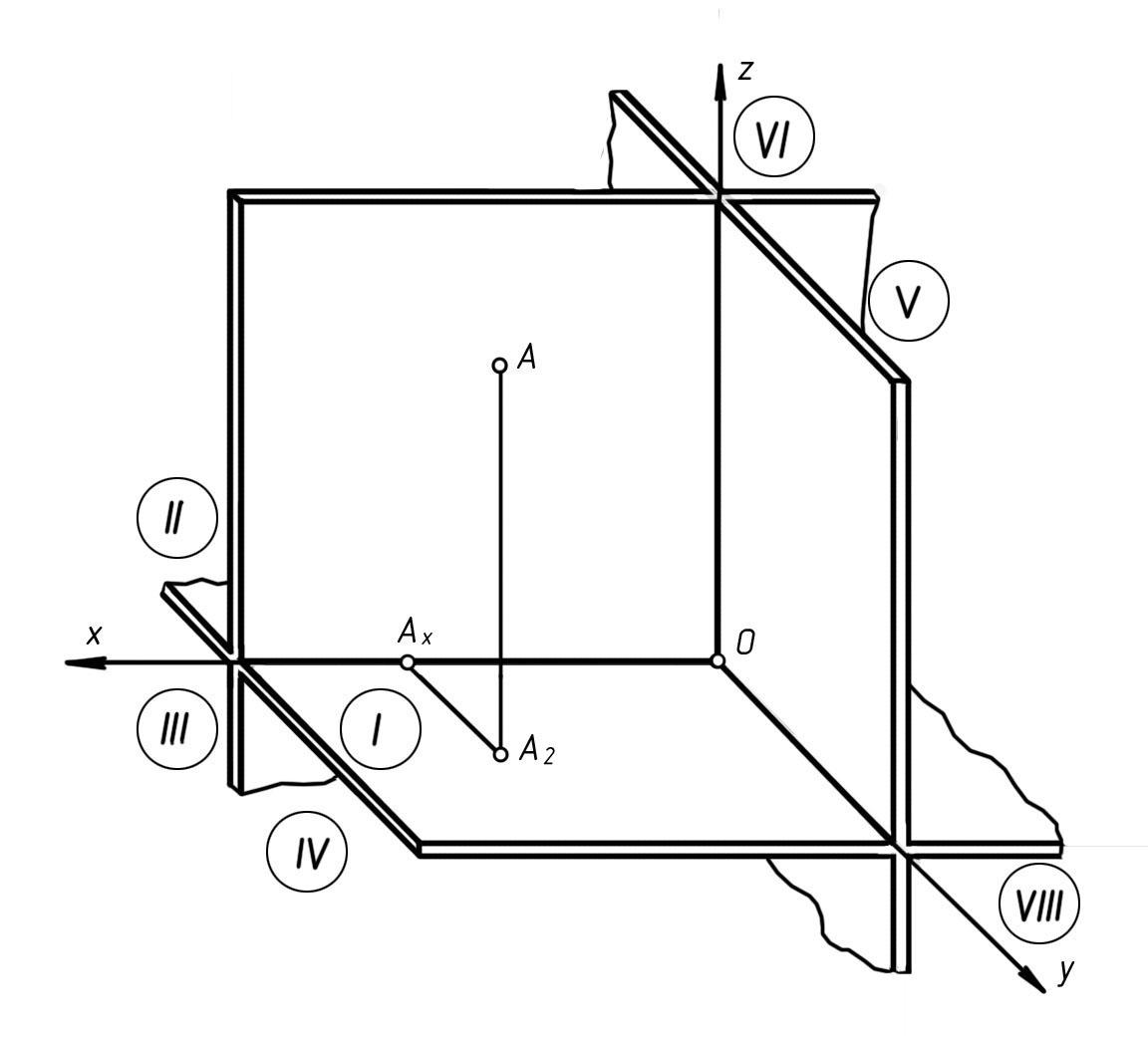

Рис. 22

Измеряя координатные отрезки единицей длины l, получим три числа, выражающих длины соответствующих координатных отрезков, – координаты точки А: абсциссу , ординату и аппликату .

Так как координаты точки А выражают также расстояния этой точки от координатных плоскостей, то, рассматривая эти плоскости как плоскости проекций, можно называть координаты точки соответственно х – ее широтой, у – глубиной и z – высотой.

Если точка А задана своим комплексным чертежом (рис. 23), то для отнесения ее к системе координат Оxyz нужно сначала построить на комплексном чертеже координатные оси. Обычно систему координат располагают так, чтобы координатные плоскости были параллельны соответствующим плоскостям проекций, при этом параллельно горизонтальной плоскости проекций задают координатную плоскость хОу. Тогда координатные оси на комплексном чертеже изобразятся так, как показано на рис. 23. Измеряя единицей длины l широту х точки А на виде спереди или на виде сверху, что все равно, ее глубину у – на виде сверху и высоту z – на виде спереди, получим координаты х, у и z точки А.

Чтобы построить точкуА (х, у, z), нужно при помощи единицы длины l определить координатные отрезки точки А, затем отложить отрезок, соответствующий координате х на оси х, а отрезки, соответствующие координатам y и z, – параллельно осям у и z (рис. 22). Конец А координатной ломаной и определит искомую точку. В зависимости от знаков координат точка может оказаться в том или другом октанте. Имея координаты точки А, единицу длины l и комплексный чертеж системы координат Oxyz, нетрудно построить комплексный чертеж точки А (рис. 23).

Пример. Построить комплексный чертеж точки А (15, 10, 20) в трех видах, если единица длины l = 1 мм (рис. 24).

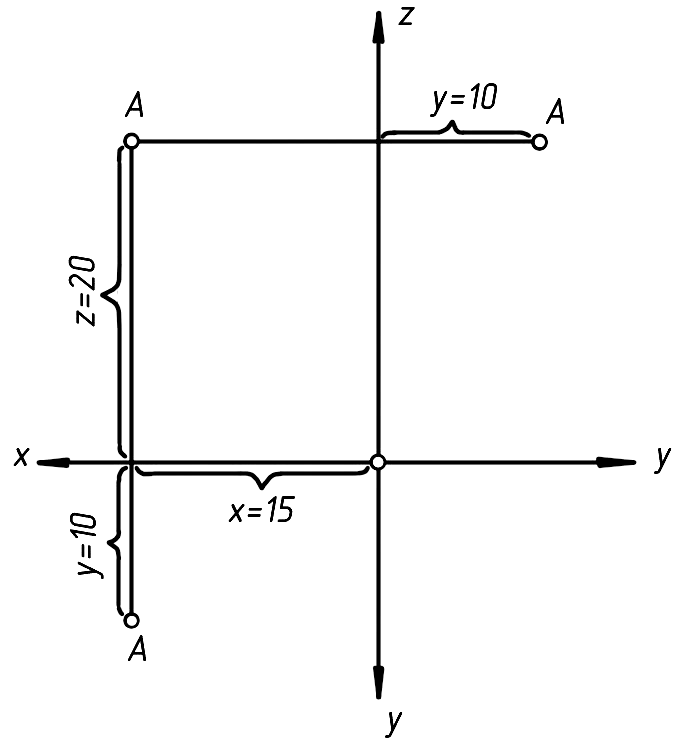
Рис. 24

Если у оригинала нет явно выраженных размерных баз (осей или плоскостей), которые удобно принять за оси или плоскости координат, то после соответствующего выбора системы координат можно принять за плоскости проекций сами координатные плоскости. Тогда получим комплексный чертеж при фиксированных плоскостях проекций, на котором будут совмещены: ось х – на видах спереди и сверху, а ось z – на видах спереди и слева.

Само построение точки А на трех видах сводится к построению координатных отрезков, соответственно равных 15, 10 и 20 мм. Точка А на виде сверху определяется координатами х и у, на виде спереди – у и z и на виде слева – у и z.