Обозначения

1. Точки пространства: прописные буквы латинского алфавита: А, В, С… или цифры 1, 2, 3…

2. Прямые и кривые линии пространства: строчные буквы латинского алфавита: a, b, c, d…; если прямая определена двумя точками А и В, то (АВ).

3. Отрезки прямых: [АВ], [1–2]; их длины соответственно: АВ, 1–2.

4. Плоскости и поверхности: прописные буквы русского алфавита, отличающиеся по написанию от латинских букв, например, Б, Г, Д, Ж …

5. Линии уровня: горизонталь –h, фронталь – f, профильная – p; плоскости уровня: горизонтальная – Г, фронтальная – Ф, профильная – П.

6. Углы:ABC,  В, , , ; их величины – ABC, В, , ,  …

7. Двугранные углы: (А, ВС, D), l, (Б, Ж).

8. Величины углов между прямыми, прямой и плоскостью, плоскостями соответственно: (a, b), (a, Б), (Б, Ж).

9. Величины расстояний между точкой и прямой, точкой и плоскостью, между прямыми и между плоскостями соответственно: А, a, А, Б, a, b, Б, Ж.

10. Последовательность точек, линий, поверхностей, фигур – верхним индексом, например, последовательность точек А: А¹, А², А³…

11. Новые положения точки А, прямой a и плоскости Б после преобразования соответственно: ; после двух преобразований: .

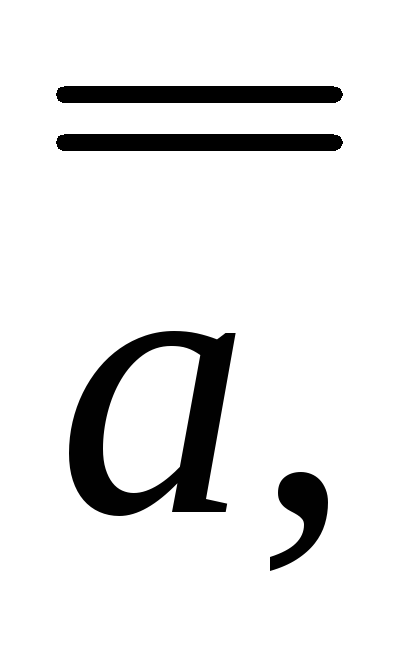
12. Принадлежность точки и линии (прямой), точки и поверхности (плоскости) – знак , например, A  a, А  Б.

13. Принадлежность линии (прямой) и поверхности (плоскости) –знак , например, a  Б.

14. Совпадение точек или фигур – знак =, например, A = B, или Ф¹ = Ф².

15. Конгруэнтность отрезков или фигур – знак , например, АВ  СD, Ф¹  Ф².

16. Пересечение фигур – знак ∩, например, a ∩ b, a ∩ Б, Б ∩ Ж.

17. Параллельность – знак //, например, a // b, a // Б, Б // Ж.

18. Перпендикулярность – знак , например, a  b, a  Б, Б  Ж.

19. Скрещивание прямых – знак ·, например,a · b.

20. Отрицание – знак /, например,A a, a Б, А В, a // b.

21. Плоскость проекций – П'.

22. При образовании комплексного чертежа плоскости видов обозначают 1, 2, 3, 4, 5, 6 ... при этом плоскости видов спереди и сзади – соответственно 1 и 6, плоскости видов сверху и снизу – 2 и 5 и плоскости видов слева и справа – 3 и 4.

23. Точки, линии и поверхности на любом виде обозначаются так же, как они обозначены в пространстве; вырожденные виды плоскостей, перпендикулярных какой-либо плоскости уровня: Б – Б, Г – Г, Д – Д…

24. Для указания способа задания плоскости рядом с ее буквенным обозначением в скобках пишутся обозначения тех элементов, которыми она задана, например: Б(АВС), Д(a ∩ b), Ж(с // d).

Глава I комплексный чертеж точки, прямой и плоскости

§ 1. Основные свойства проецирования

1. Центральная проекция (перспектива). Пусть дана некоторая плоскость П', которую называют плоскостью проекций, и вне ее точка S, называемая центром проекций.

Для построения изображения, или, как говорят, проекции А' некоторой точки А, проводят через точку А и центр проекций S прямую SA, называемую проецирующей прямой, а затем находят точку А' пересечения этой прямой с плоскостью П' (рис. 1)^. Таков метод центрального проецирования точек пространства на плоскость проекций П'. Его можно записать с помощью следующего символического равенства: A' = П' ∩ (SA) (A' есть точка пересечения плоскости П' с прямой SA).

Рис. 1

Проецирование можно выполнить для любой точки пространства, за исключением точек, лежащих в плоскости, проходящей через центр проекций S и параллельной плоскости проекций П'.

На рис. 1 показано построение проекций точек А, В, С и D, различно расположенных относительно плоскости проекций П' и центра проекций S.

Обычно проекциями точек, лежащих в плоскости, проходящей через центр проекций S и параллельной плоскости проекций П', принято считать бесконечно удаленные точки^ плоскости П', так как для этих точек проецирующие прямые оказываются параллельными плоскости проекций П'. Однако для центра проекций S не может быть построена проекция, так как проецирующая прямая становится при этом неопределенной, вместе с тем становится неопределенной и проекция точки S на плоскости П'.

Так как каждая геометрическая фигура есть некоторая совокупность точек, то будем называть проекцией фигуры совокупность проекций всех ее точек. Однако для построения проекции фигуры совершенно не обязательно проецировать все ее точки. Так, проекция отрезка или прямой линии вполне определяется проекциями двух точек; проекция треугольника или плоскости – проекциями трех точек; проекция какого-либо многогранника – проекциями его вершин.

Изображение предметов при помощи центрального проецирования обладает наглядностью, так как человеческое зрение в геометрическом отношении совпадает с операцией центрального проецирования (оптический центр хрусталика глаза можно считать центром проекций, а участок задней стенки сетчатки может быть принят приближенно за плоскость проекций). Однако метод центрального проецирования слишком сложен и в значительной степени искажает форму и размеры оригинала, так как не сохраняет параллельности прямых и отношения отрезков. Поэтому на практике чаще пользуются методом параллельного проецирования (в частности, ортогонального проецирования). Этот метод, являясь частным случаем центрального проецирования, когда центр проекций находится в бесконечно удаленной точке S, дает более простое построение изображения и в большей степени, как это будет показано дальше, сохраняет те свойства оригинала, от которых зависят его форма и размеры.

2. Параллельная проекция. Пусть даны плоскость проекций П' и направление проецирования s, непараллельное плоскости проекций. Когда мы перемещаем центр проекций S в бесконечно удаленную точку S_m, то все проецирующие прямые как пересекающиеся в бесконечно удаленной точке будут параллельны некоторому направлению s. Чтобы построить проекцию А' какой-либо точки А, через нее проводят проецирующую прямую параллельно направлению проецирования s, а затем находят точку А' пересечения этой прямой с плоскостью П' (рис. 2).

Таков метод параллельного проецирования точек пространства на плоскость проекций. Рассмотрим некоторые свойства параллельной проекции:

1. Проекцией точки является точка. Это свойство следует из самого способа построения проекции точки.

2. Проекцией прямой линии является прямая линия. Все прямые, проецирующие точки А, В, С данной прямой l (рис. 2), лежат в одной плоскости, проходящей через прямую l и параллельной направлению проецирования s. Эта плоскость, называемая проецирующей плоскостью, пересекает плоскость проекций П' по прямой линии l', которая, согласно определению проекции фигуры как совокупности проекций всех ее точек, и является проекцией данной прямой. Это свойство будем называть свойством прямолинейности.

Очевидно, что если прямая l будет проецирующей прямой, то ее проекция выродится в точку.

Рис. 2

3. Проекцией точки, лежащей на некоторой прямой, является точка, лежащая на проекции данной прямой. Это свойство, называемое свойством принадлежности, непосредственно следует из определения проекции фигуры как совокупности проекций всех ее точек.

Рассмотренные три свойства имеют место также и в случае центральной проекции. Однако параллельная проекция обладает еще другими свойствами, которых не имеет центральная проекция (рис. 2).

Таковы следующие свойства:

4. Проекциями параллельных прямых являются параллельные прямые. Действительно, если прямые k и l параллельны, то и проецирующие их плоскости будут параллельны как содержащие по паре пересекающихся соответственно параллельных прямых (k // l и АА′ // ММ'). Отсюда следует, что k′ // l′ как прямые пересечения параллельных плоскостей третьей плоскостью. Это свойство называется свойством сохранения параллельности. Очевидно, что если прямые k и l будут проецирующими прямыми, то указанное свойство теряет смысл, так как проекциями этих прямых будут две точки.

5. Отношение проекций отрезков, лежащих на параллельных прямых или на одной и той же прямой, равно отношению самих отрезков. Пусть АВ и MN – отрезки, лежащие на параллельных прямых k и l, а А'В' и M'N' – их проекции на плоскость П' (см. рис. 2). Проведем в проецирующих плоскостях отрезки АВ* и MN*, соответственно параллельные отрезкам А'В' и M'N'. При этом [АВ*]  [А'В′] и [MN*]  [M'N′]. Очевидно, что треугольники ABB* и MNN* подобны, так как их соответственные стороны параллельны. Отсюда получаем: [А'В'] : [М'N'] = [AB*] : [MN*] = = [АВ] : [MN]. Если данные отрезки лежат на одной прямой, то теми же рассуждениями можно установить, что А'В' : В'С' = АВ : ВС.

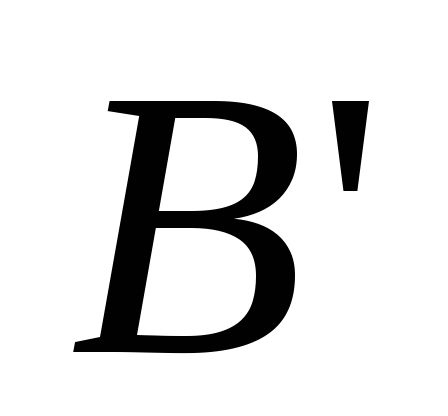
6. Проекция фигуры не меняется при параллельном переносе плоскости проекций. В качестве проецируемой фигуры возьмем треугольник ABC и спроецируем его по направлению s на плоскости П' и , параллельные между собой (рис. 3). Так как отрезки,и параллельны и конгруэнтны, то четырехугольники и являются параллелограммами, следовательно, треугольники и конгруэнтны.

Очевидно, что эти же рассуждения применимы для проекции любой другой фигуры.

Рис. 3

Рассматривая указанные выше свойства параллельной проекции, можно заметить, что ее свойства 4, 5 и 6 обеспечивают более простое построение изображения, которое вместе с тем меньше искажает форму и размеры оригинала по сравнению с центральной проекцией.

В самом деле, свойство 4 указывает на сохранение параллельности прямых, поэтому параллельная проекция трапеции есть трапеция, а параллельная проекция параллелограмма есть параллелограмм, в то время как в центральной проекции эти фигуры вообще проецируются в четырехугольники произвольного вида. По свойству 5 мы имеем для проекций двух параллельных отрезков соотношение IА'В'I : IМ'N'I = IABI : IMNI, откуда IA'B'I : IАВI = IM'N'I : IMNI (см. рис. 2), т. е. при параллельном проецировании искажение для всех параллельных отрезков постоянно. Отсюда, в частности, следует, что середина отрезка проецируется в середину проекции отрезка.

Свойство 6 позволяет переносить плоскость проекций параллельно самой себе, т. е. отказаться от фиксации плоскости проекций. При этом говорят, что положение плоскости проекций определяется лишь с точностью до параллельности. Это обстоятельство весьма удобно и поэтому широко применяется при построении технического чертежа.

3°. Ортогональная проекция. Еще большее упрощение построения чертежа дает применение ортогонального проецирования, являющегося частным случаем параллельного проецирования, когда направление проецирования s перпендикулярно плоскости проекций П'. В этом случае нетрудно установить соотношение между длиной натурального отрезка и длиной его проекции. Если отрезок АВ образует с плоскостью проекций угол α, то, проведя IАВ*I // IА'В'I (рис. 4), получим из прямоугольного треугольника АВ*В:

IAВ*I = IABIcos  или IА'В'I = IABIcos .

Ортогональная проекция получила наибольшее распространение в технических чертежах, так как она позволяет наиболее легко судить о размерах изображаемых предметов.

Рис. 4

Рассмотренные выше методы проецирования позволяют однозначно решать прямую задачу, т. е. по данному оригиналу строить его проекционный чертеж. Однако обратная задача – по данному проекционному чертежу воспроизвести (реконструировать) оригинал – не решается однозначно. Эта задача допускает бесчисленное множество решений, так как каждую точку А' плоскости проекций П' можно считать проекцией любой точки проецирующей прямой, проходящей через А' (см. рис. 1, 2 и 4). Таким образом, рассмотренные нами проекционные чертежи не дают возможности определить оригинал, или, как говорят, не обладают свойством «обратимости». Для получения обратимых чертежей дополняют проекционный чертеж необходимыми данными. Существуют различные методы такого дополнения. В данном курсе будут применяться только два вида обратимых чертежей, а именно: комплексные чертежи в ортогональных проекциях и аксонометрические чертежи как получившие наибольшее распространение.