§ 3. Многогранные поверхности

Как известно, многогранной поверхностью называется поверхность, состоящая из ряда плоских многоугольников, в частности, из треугольников или параллелограммов. Элементами многогранной поверхности являются ее вершины, ребра и грани.

Из многогранных поверхностей на практике наиболее часто встречаются призматические и пирамидальные поверхности. Тело, ограниченное замкнутой многогранной поверхностью, называется многогранником. Заслуживают внимания правильные многогранники, состоящие из правильных многоугольников.

На комплексном чертеже многогранники задаются своими вершинами и ребрами, при этом, выполняя условия видимости, невидимые ребра изображают штриховыми линиями. Кроме этого, рекомендуется вершины многогранника отмечать кружками, в отличие от конкурирующих точек на скрещивающихся ребрах, которые оставляют неотмеченными. Для облегчения реконструкции многогранника рекомендуется обозначать его вершины.

Если у многогранника некоторые из его ребер являются профильными прямыми или прямыми, перпендикулярными плоскостям уровня, а вершины не обозначены, то при реконструкции многогранника по комплексному чертежу можно получить не одно, а несколько решений. В самом деле, если задан комплексный чертеж куба (рис. 49а), на котором нет обозначений вершин, то при реконструкции, помимо куба (рис. 49б) можно получить четыре различно расположенные в пространстве треугольные призмы (одна из этих призм изображена на рис. 49в), четверть кругового цилиндра (рис. 49г), фигуру, дополняющую четверть кругового цилиндра до куба (рис. 49д) и др. Для устранения многозначности в этом случае необходимо обозначить все вершины куба.

Таким образом, если у многогранника имеются ребра профильного положения или ребра, перпендикулярные плоскостям уровня, а также при совпадении каких-нибудь вершин или ребер на каком-нибудь виде обратимость чертежа достигается либо введением буквенных обозначений вершин многогранника, либо построением вида слева многогранника или какого-нибудь другого дополнительного его вида^.

а

б

г

д

в

Рис. 49

§ 14. Поверхности вращения

1. Поверхностью вращения называется поверхность, которая описывается какой-либо кривой (образующей) при ее вращении вокруг неподвижной оси. Образующая может быть как плоской, так и пространственной кривой. Поверхность вращения определяется заданием своей образующей l и оси i (рис. 50).

Каждая точка L образующей l при вращении описывает окружность с центром на оси i. Эти окружности называются параллелями.

Наибольшая и наименьшая параллели называются экватором и горлом соответственно. У поверхности, изображенной на рис. 50а, параллели h² и h⁵ являются экваторами, а параллель h³ – горлом.

Кривые, которые получаются в сечении поверхности вращения плоскостями, проходящими через ось i, называются меридианами. Все меридианы равны между собой.

При изображении поверхности вращения на комплексном чертеже обычно поверхность располагают так, чтобы ее ось i была перпендикулярна к плоскости уровня. Ось i вертикальная, тогда все параллели на виде сверху не искажаются, причем экватор h⁵ и горло h³ определяют очерк поверхности на виде сверху (рис. 50б). Меридиан f, расположенный во фронтальной плоскости, не искажается на виде спереди. Этот меридиан называется главным меридианом, он определяет очерк поверхности на виде спереди.

а

б

Рис. 50

Чтобы выделить какую-нибудь точку М на поверхности вращения, выбираем ее на виде спереди, после чего при помощи параллели h⁴, проведенной на уровне точки М, легко построить ее и на виде сверху. На рис. 50 точка М предполагается видимой на виде спереди.

Поверхности вращения получили самое широкое применение в деталях различных механизмов и машин. Основными причинами этого является, с одной стороны, распространенность вращательного движения, а с другой – простота обработки поверхностей вращения.

Клапан двигателя, ограниченный поверхностями вращения различных видов, а именно: сферической 1, торовой 2, конической 3 и цилиндрической 4, – показан на рис. 51.

Рис. 51

Рассмотрим образование этих и других частных видов поверхностей вращения.

2. Сначала рассмотрим поверхности, образуемые вращением прямой линии.

1. Цилиндр вращения образуется вращением прямой l вокруг параллельной ей оси i (рис. 52).

2. Конус вращения образуется вращением прямой l вокруг пересекающейся с ней оси i (рис. 53).

3. Однополостный гиперболоид вращения образуется вращением прямой l вокруг скрещивающейся с ней оси i (рис. 54).

При вращении прямой l вокруг оси i все точки прямой опишут окружности различных радиусов, причем общий перпендикуляр АО прямых l и i будет наименьшим из всех радиусов, и поэтому точка А опишет окружность, являющуюся горлом гиперболоида. Для построения главного меридиана гиперболоида достаточно повернуть вокруг оси i ряд точек прямой l до совмещения их с фронтальной плоскостью, проходящей через ось i. Тогда получим гиперболу, которая и будет очерком на виде спереди гиперболоида.

а

б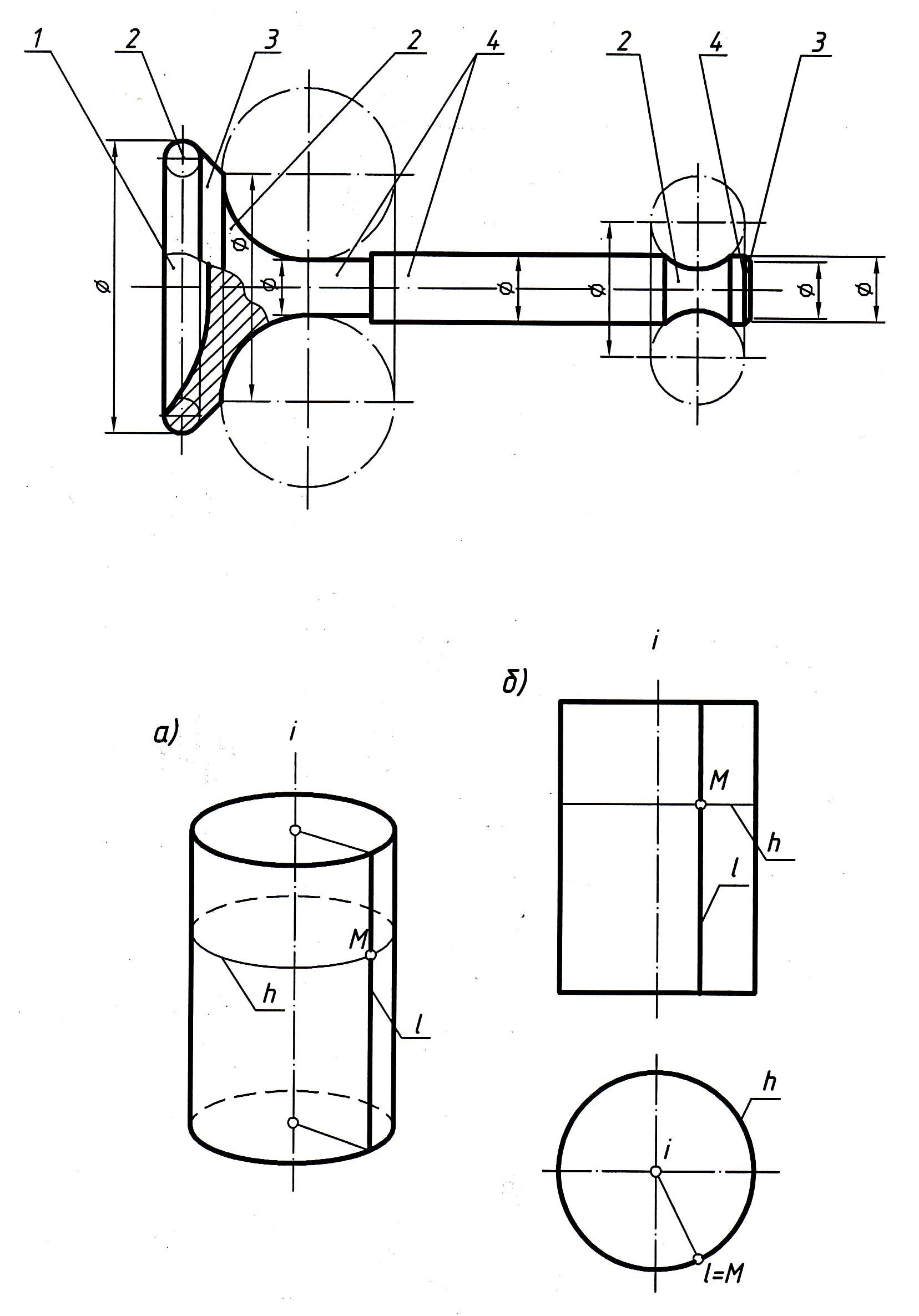

Рис. 52

Рассмотренные поверхности вращения можно отнести и к классу линейчатых поверхностей, так как они образованы движением прямой линии. Кроме того, эти поверхности являются поверхностями второго порядка; максимальное число точек пересечения каждой из этих поверхностей с прямой линией равно двум.

Построение точки М на любой из рассмотренных выше поверхностей вращения (рис. 52–54) можно выполнить либо при помощи параллели h, либо прямолинейной образующей l.

Все три указанные поверхности вращения применяются при передаче вращения с помощью зубчатых или фрикционных колес. Так, передача вращения производится:

при параллельных осях с помощью цилиндрических колес (рис. 55а),

пересекающихся – конических колес (рис. 55б),

скрещивающихся – гиперболоидальных колес (рис. 55в).

а

б

а

б

Рис. 53 Рис. 54

а

б

в

Рис. 55

3. Рассмотрим поверхности, образуемые вращением окружности:

1. сфера образуется вращением окружности вокруг ее диаметра i;

2. тор образуется вращением окружности вокруг оси i, лежащей в плоскости окружности, но не проходящей через ее центр (рис. 56). При этом если ось i проходит вне окружности, то тор называют кольцом (рис. 57).

а

б

Рис. 56

а

б

Рис. 57

Сфера является поверхностью второго порядка, а тор – четвертого, что соответствует максимальному числу точек пересечения этих поверхностей с прямой линией.

Построение точки М как на сфере, так и на торе производят с помощью параллели h.

4. В заключение рассмотрим поверхности, образуемые вращением кривых второго порядка – эллипса, параболы и гиперболы вокруг их осей.

1

б

.Эллипсоид вращения образуется вращением эллипса вокруг его оси i (рис. 58).

а

Рис. 58

2. Параболоид вращения образуется вращением параболы вокруг ее оси i (рис. 59) (параболоид вращения употребляется в качестве отражающей поверхности в прожекторах для получения параллельного светового пучка).

3. Однополостный гиперболоид вращения образуется вращением гиперболы вокруг ее мнимой оси i (рис. 60).

4. Как было показано, однополостный гиперболоид вращения является линейчатой поверхностью и может быть образован вращением прямой линии вокруг скрещивающейся с ней оси (см. рис. 54). На рис. 60, помимо гиперболоида, показан его асимптотический конус вращения, образованный вращением асимптот гиперболы, являющейся образующей гиперболоида. Во внешней части этого конуса и расположен однополостный гиперболоид.

5. Двухполостный гиперболоид вращения образуется вращением гиперболы вокруг ее действительной оси i (рис. 61).

При вращении асимптот этой гиперболы получаем асимптотический конус вращения, во внутренней области которого и расположен двухполостный гиперболоид.

Рассмотренные выше четыре поверхности являются поверхностями второго порядка; максимальное число точек пересечения каждой из этих поверхностей с прямой линией равно двум.

а

б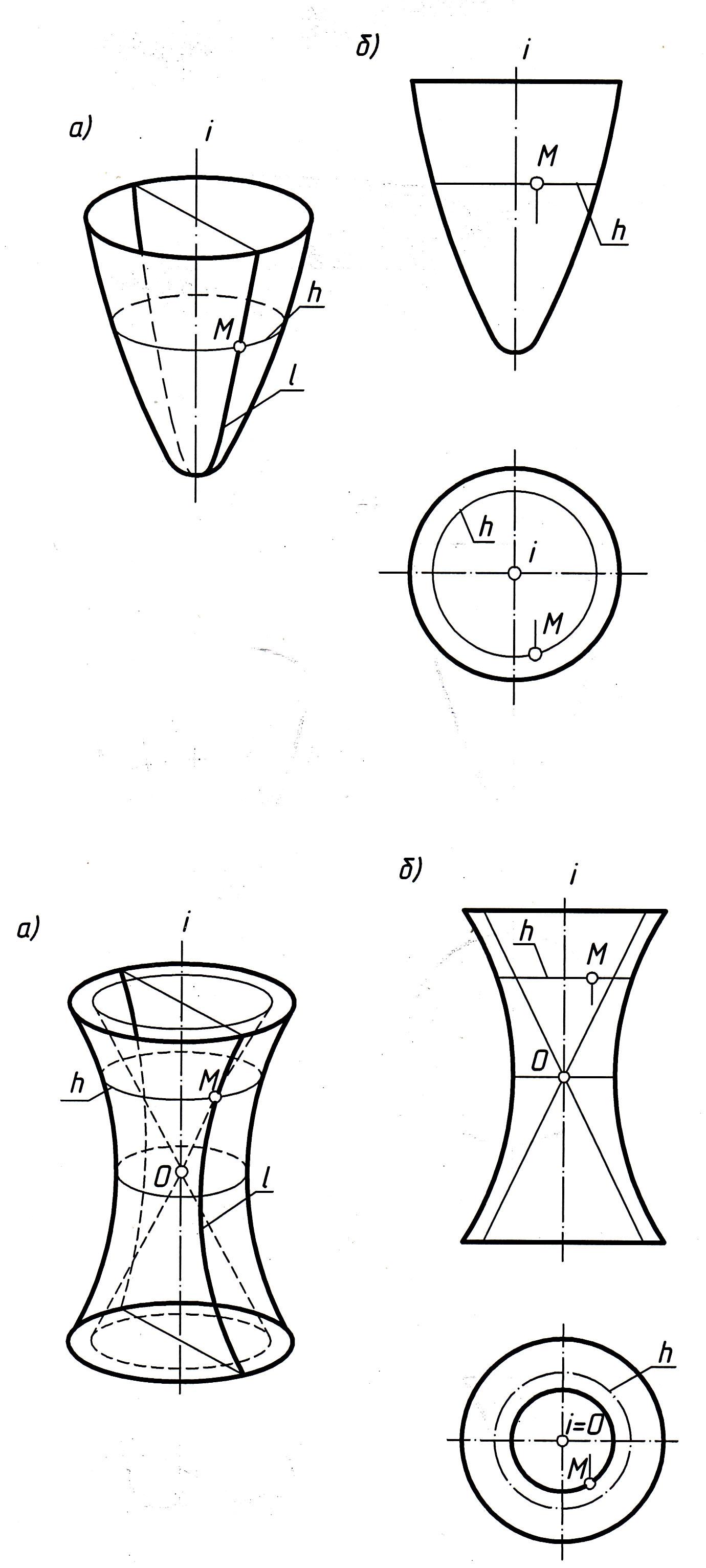

Рис. 59

а

б

Рис. 60

Построение точки М на каждой из этих поверхностей производится с помощью их параллелей h (см. рис. 58–61).

а

б

Рис. 61