§ 5. Способ вращения вокруг прямой, перпендикулярной плоскости уровня

1. Как уже указывалось § 2 данной главы, при применении способа вращения направления проецирования оригинала остаются неизменными, а изменяется положение оригинала в пространстве, что достигается вращением его вокруг некоторой оси. В качестве оси вращения обычно выбирают прямую, перпендикулярную какой-нибудь плоскости уровня, или прямую уровня, так как построения, выполняемые на комплексном чертеже при вращении вокруг этих прямых, значительно проще построений при вращении вокруг прямой общего положения. Если же требуется произвести вращение оригинала вокруг оси, являющейся прямой общего положения, то с помощью построения дополнительных видов сводят это вращение к вращению вокруг прямой, перпендикулярной плоскости уровня относительно одной из новых плоскостей проекций. После выполнения вращения на дополнительных видах возвращают полученные результаты на виды спереди и сверху.

При выполнении вращения вокруг какой-либо оси υ следует помнить, что вращающаяся точка А описывает окружность, расположенную в плоскости Б, перпендикулярной оси вращения υ (рис. 185). Центр С этой окружности является основанием перпендикуляра, опущенного из вращаемой точки А на ось вращения υ, или, иначе, точкой пересечения с осью вращения υ плоскости Б, в которой вращается точка. Совершенно очевидно, что все точки оригинала при его вращении вокруг оси поворачиваются на один и тот же угол ω. Исключение составляют те точки оригинала, которые расположены на оси вращения; эти точки при вращении остаются неподвижными.

υ

Рис. 185

2. Вращение точки вокруг прямой, перпендикулярной плоскости уровня. Пусть дана какая-нибудь точка А, которая вращается вокруг вертикальной прямой i. Плоскость Г, в которой точка А описывает окружность, будучи перпендикулярной к вертикальной прямой i, будет горизонтальной плоскостью уровня (рис. 186а). Окружность с центром в точке С, которую при вращении описывает точка А, изображается на виде сверху без искажения, а на виде спереди – в виде отрезка прямой, перпендикулярной линиям связи. Для упрощения наглядного изображения на рис. 186а плоскость 2 совмещена с горизонтальной плоскостью Г, а на рис. 187а плоскость 1 совмещена с фронтальной плоскостью Ф.

а

б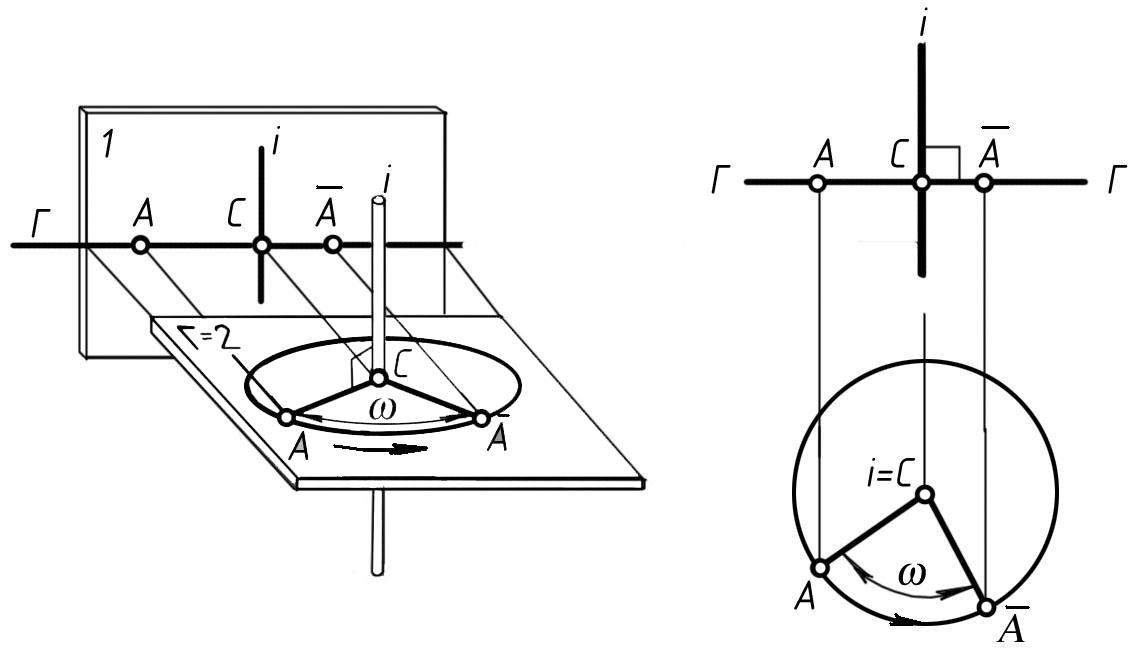

Рис. 186

Для примера выполним поворот точки А вокруг прямой i на некоторый угол ω по направлению, противоположному движению часовой стрелки (если смотреть сверху, рис. 186б). Для этого проводим на виде сверху окружность с центром в точке С = i и радиусом |АC|. Затем откладываем угол АСА = ω, учитывая указанное направление вращения. Получаем новое положение Ā точки А на виде сверху. На виде спереди новое положение Ā точки А определится на вырожденном виде Г–Г плоскости Г, в которой происходит вращение точки А.

Если точка А вращается вокруг прямой, перпендикулярной фронтальной плоскости, то она опишет окружность во фронтальной плоскости уровня Ф (рис. 187а). Эта окружность изобразится без искажения на виде спереди, а на виде сверху она изобразится в виде отрезка прямой, перпендикулярной линиям связи.

На рис. 187б осуществлен поворот точки А вокруг прямой i, перпендикулярной фронтальной плоскости на угол ω по направлению движения часовой стрелки.

Рис. 187

Таким образом, при вращении точки вокруг прямой, перпендикулярной фронтальной (горизонтальной) плоскости, точка на виде спереди (сверху) перемещается по окружности, а на виде сверху (спереди) – по прямой, перпендикулярной линиям связи.

3. Вращение прямой линии. Так как прямая линия определяется двумя своими точками, то вращение прямой сводится к вращению точек, определяющих прямую.

Пусть, например, требуется повернуть прямую общего положения вокруг вертикальной прямой i на угол ω по направлению, противоположному движению часовой стрелки (рис. 188).

Выбрав на прямой l две произвольные точки 1 и 2, повернем их вокруг оси i на один и тот же угол ω по заданному направлению вращения (на виде сверху хорда 1–должна быть равна хорде между точками, отмеченными крестиками). Новые положенияи точек 1 и 2 определят новое положение данной прямойl после ее поворота на угол ω в данном направлении. Рассматривая на виде сверху треугольники 1–2–i и ––i, замечаем, что стороны 1–i и 2–i первого треугольника соответственно равны сторонам –i и –i второго треугольника, углы, заключенные между этими сторонами, также равны. Поэтому Δ1–2–i Δ––i и, значит, |1–2| = |–|.

Рис. 188

Таким образом, при вращении на один и тот же угол двух точек вокруг вертикальной прямой расстояние между ними на виде сверху остается неизменным.

Очевидно, что при вращении вокруг прямой, перпендикулярной фронтальной плоскости, остается неизменным расстояние между точками на виде спереди.

Эти свойства позволяют несколько упростить построение нового положения прямой после ее поворота. Поворот прямой l вокруг вертикальной прямой i на угол ω по направлению, противоположному движению часовой стрелки, выполнен с применением упрощенных построений на рис. 189. Так же, как и раньше, прямая l определена двумя точками. При этом точка 1 выбрана произвольно на прямой l, а точка 2 является основанием общего перпендикуляра прямых l и i. Точка 2 повернута вокруг прямой i на угол ω в заданном направлении. После этого через новое положение точки 2 на виде сверху проводим перпендикулярно к отрезку i– новое положение прямой l на этом виде. Так как отрезок 1–2 при вращении не меняет своей длины, то откладываем на от точки отрезок |–| = |2–1|, чем определяется новое положение точки 1 на виде сверху. По точкам и на виде сверху находим эти точки на виде спереди. Точки и определяют прямую l в новом положении .

Рис. 189

4. Вращение плоскости. Так как плоскость определяется тремя своими точками, не лежащими на одной прямой, то вращение плоскости сводится к вращению этих точек.

Пусть, например, требуется повернуть плоскость Б (ABC) общего положения вокруг прямой i, перпендикулярной фронтальной плоскости на угол ω по направлению движения часовой стрелки (рис. 190).

Повернув точки А, В и С, определяющие данную плоскость, на один и тот же угол ω по заданному направлению вращения (на виде спереди хорда АĀ должна быть равна хорде между точками, отмеченными черточками, и хорде между точками, отмеченными крестиками), получим новые положения Ā, и данных точек. Точки Ā, и определяют новое положение плоскости после ее поворота вокруг прямой i на угол ω в заданном направлении.

Так как на виде спереди треугольник ABC сохраняет свою величину при вращении вокруг прямой i, перпендикулярной фронтальной плоскости, то можно сначала повернуть одну из сторон треугольника приемом, указанным на рис. 189, тем самым найдутся новые положения двух вершин треугольника. Тогда новое положение третьей вершины можно найти из условия, что на виде спереди ΔАВС ΔĀ (рис. 190).

5. Четыре основные задачи можно решить не только методом дополнительных видов, как в в § 4 данной главы, но и методом вращения вокруг прямых, перпендикулярных плоскостям уровня, однако тогда решения получаются более громоздкими. Покажем для сравнения решения только первой и третьей задач.

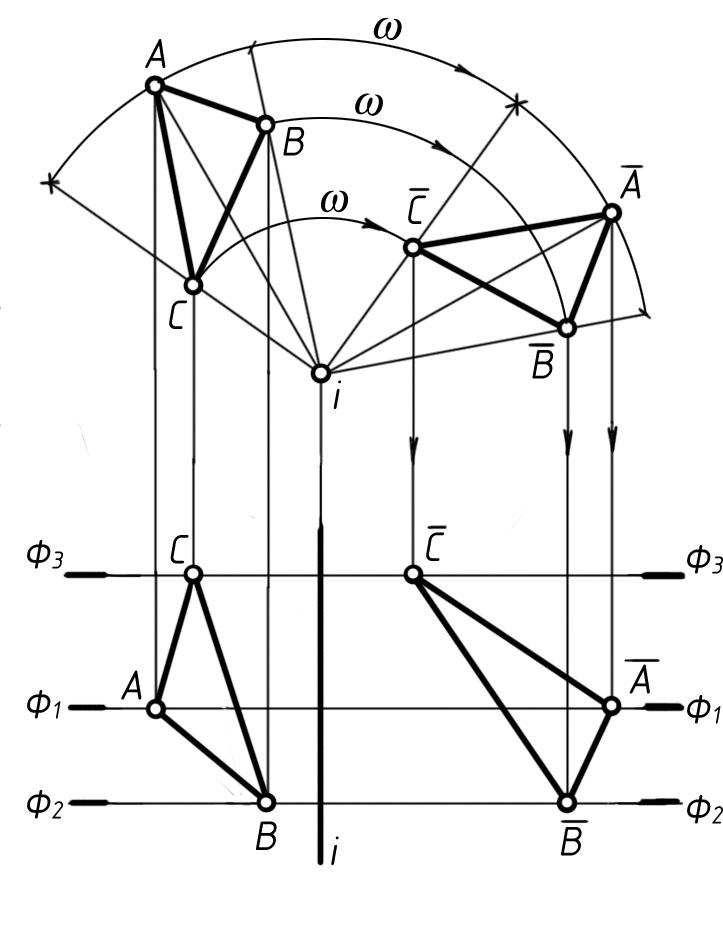
Рис. 190

Задача 1. Повернуть прямую l общего положения до положения прямой уровня.

Повернем прямую l до фронтального положения. Для этого за ось вращения примем вертикальную прямую i, проходящую через какую-нибудь точку 1 прямой l (рис. 191). При таком выборе оси вращения построение несколько упростится, так как точка 1 будет неподвижной, и поэтому для поворота прямой l останется повернуть только одну точку, например, точку 2. Так как на виде сверху прямая l в своем новом положении должна быть перпендикулярна к линиям связи, то этим определяется угол, на который должна быть повернута точка 2. Построив новое положение точки 2, мы тем самым определим прямую l в ее фронтальном положении . На виде спереди прямая не искажается, а угол β, образованный на этом виде между прямой и горизонтальной прямой, дает натуральный угол наклона прямой l к горизонтальной плоскости уровня.

Для поворота прямой l до горизонтального положения нужно за ось вращения принять прямую, перпендикулярную фронтальной плоскости уровня, проведенную через какую-нибудь точку прямой l.

Задача 2. Повернуть плоскость Б (АВС) общего положения до положения плоскости, перпендикулярной какой-нибудь плоскости уровня.

Повернем плоскость Б, например, до положения наклонной плоскости. Для этого ее нужно повернуть вокруг вертикальной прямой i так, чтобы какая-нибудь горизонталь h плоскости Б стала перпендикулярна фронтальной плоскости уровня (рис. 192).

Рис. 191 Рис. 192

Так как на виде сверху горизонталь h займет положение , параллельное линиям связи, то на виде сверху определяется угол поворота ω = (h ^ ). Если теперь повернуть на этот угол вокруг оси i, проходящей через точку В, точки А и С, то новые положения этих точек Ā и совместно с неподвижной точкой В определят новое положение плоскости Б. Это будет наклонная плоскость. На виде спереди точки плоскости Б в их новых положениях расположатся на одной прямой –, которая и будет видом спереди плоскости. Угол β между вырожденным видом –нового положения плоскостиБ и горизонтальной прямой дает натуральный угол наклона плоскости Б к горизонтальной плоскости.

Для поворота плоскости Б до вертикального положения нужно за ось вращения принять прямую, перпендикулярную фронтальной плоскости, проведенную через какую-нибудь точку плоскости Б. При этом поворот надо осуществить так, чтобы какая-нибудь фронталь плоскости Б стала вертикальной прямой.

6. В заключение решим два примера. В первом из этих примеров способ вращения используется для преобразования комплексного чертежа, а во втором – для решения кинематической задачи.

Пример 1. На прямой а общего положения от ее точки А отложить отрезок АВ данной длины l (рис. 193).

Выберем на прямой а произвольную точку 1, отличную от данной точки А, и повернем прямую а до фронтального положения вокруг вертикальной прямой i, проходящей через точку А. Так как на виде спереди прямая не искажается, то, отложив на этой прямой отрезок АВ заданной длины l и произведя обратный поворот, найдем на прямой а искомую точку В. Возможны два решения, так как на прямой а можно отложить отрезок АВ по разные стороны от точки А.

Решение данного примера свелось к решению рассмотренной выше первой задачи (см. п. 5).

Пример 2. Повернуть данную точку М вокруг данной вертикальной прямой i до совмещения ее с плоскостью Б (a // b) (рис. 194).

Рис. 193 Рис. 194

При вращении вокруг прямой i точка М опишет окружность в горизонтальной плоскости Г. Поэтому при совмещении с плоскостью Б точка М расположится на линии пересечения плоскостей Б и Г, т. е. на горизонтали h плоскости Б. Проведя из центра i на виде сверху окружность радиусом [iM], получим в пересечении с горизонталью h точки и – новые положения на виде сверху точки М. На виде спереди эти точки найдутся на вырожденном виде Г–Г плоскости Г.

Итак, точки и являются новыми положениями точки М, повернутой соответственно на углы ω₁ и ω₂ до совмещения с плоскостью Б.

Если на виде сверху горизонталь h касалась бы окружности, тогда задача имела бы одно решение, а если бы она проходила вне окружности, то задача не имела бы решения.