§ 5. Взаимное пересечение поверхностей второго порядка. Особые случаи пересечения
1. Так как поверхности второго порядка часто встречаются в технической практике, то вопрос об их взаимном пересечении заслуживает особого рассмотрения.
Линия пересечения двух поверхностей второго порядка является кривой четвертого порядка, т. е. эта кривая пересекается с плоскостью в четырех точках (действительных и мнимых). В частных случаях линия пересечения поверхностей второго порядка может распадаться, причем особый интерес представляет случай ее распадения на пару плоских кривых второго порядка.
Для примера рассмотрим пересечение сферы с конической поверхностью второго порядка, имеющей круговое основание АВ, расположенное на данной сфере (рис. 153). В этом случае линия пересечения распадается на две окружности: данную окружность АВ и окружность CD, которые изображаются на виде спереди в виде отрезков прямых, так как плоскость симметрии конической поверхности параллельна фронтальной плоскости.
Выясним условия, при которых линия пересечения двух поверхностей второго порядка распадается на пару плоских кривых второго порядка.
Если две поверхности имеют в какой-либо их общей точке одну и ту же касательную плоскость, то они касаются между собой в этой точке. Когда две пересекающиеся поверхности имеют две точки, в которых они касаются друг друга, то говорят, что такие поверхности имеют двойное прикосновение.
Линия пересечения двух поверхностей второго порядка, имеющих двойное прикосновение, распадается на пару кривых второго порядка, плоскости которых проходят через прямую, соединяющую точки прикосновения.
Рассмотрим пример, иллюстрирующий это положение.
Пример 1. Построить линию пересечения двух цилиндрических поверхностей вращения одинакового диаметра (рис. 154).
Данные поверхности имеют двойное прикосновение в точках А и В, так как в этих точках обе поверхности имеют общие касательные плоскости Ф1 и Ф2. Поэтому линия их пересечения распадается на пару кривых второго порядка, которые должны проходить через точки прикосновения А и В и точки С, F и D, Е пересечения контурных образующих.
Нетрудно видеть, что линия пересечения в данном случае будет представлять собой два одинаковых эллипса, большими осями которых будут CF и DE, а малыми – АВ. Эти эллипсы изображаются на виде спереди отрезками прямых СF и DЕ, а на виде сверху – окружностью, совпадающей с вырожденным видом цилиндрической поверхности.
Рис. 153 Рис. 154
2. Теорема о двойном прикосновении позволяет весьма просто строить круговые сечения тех поверхностей второго порядка, которые их имеют. Для этого следует провести сферу, имеющую двойное прикосновение с данной поверхностью. Тогда линия их пересечения распадается на пару плоских кривых. Но так как плоские кривые, расположенные на сфере, – окружности, то этим самым будут найдены круговые сечения поверхности второго порядка.
Итак, для построения круговых сечений поверхностей второго порядка следует провести сферу, имеющую двойное прикосновение с данной поверхностью, тогда линия их пересечения даст пару круговых сечений данной поверхности.
Рассмотрим примеры.
Пример 2. Построить круговые сечения эллиптического цилиндра (рис. 155).
Из какой-либо точки О оси цилиндра описываем сферу так, чтобы она касалась двух образующих цилиндра и пересекала бы его. Точки касания М и N будут точками соприкосновения обеих поверхностей, так как в них можно провести общие касательные плоскости Ф1 и Ф2. Таким образом, имеем двойное прикосновение поверхностей второго порядка и, следовательно, линия пересечения распадается на пару плоских кривых, в данном случае – на пару окружностей АВ и CD, расположенных в наклонных плоскостях. Полученные два круговых сечения цилиндра входят в две серии круговых сечений цилиндра, параллельных между собой.
Рис. 155
Пример 3. Построить круговые сечения эллиптического конуса (рис. 156).
Как и в предыдущем примере, описываем сферу с центром в точке О на оси конуса так, чтобы она имела двойное прикосновение с конусом. В точках М и N у обеих поверхностей общие касательные плоскости Б1 и Б2. Тогда линия пересечения распадается на пару окружностей АВ и CD, расположенных в наклонных плоскостях. Полученные круговые сечения входят в две серии круговых сечений конуса, параллельных между собой.
Рис. 156
Пример 4. Построить круговые сечения трехосного эллипсоида (рис. 157).
Описываем сферу с центром в точке О и радиусом, равным средней полуоси эллипсоида. Тогда имеем двойное прикосновение в точках М и N и, следовательно, линия пересечения распадается на пару окружностей АВ и CD. Полученные два круговых сечения проходят через центр эллипсоида и поэтому называются центральными. Они входят в две серии круговых сечений эллипсоида, параллельных между собой.
3. Не всегда удается непосредственно обнаружить двойное прикосновение у пересекающихся поверхностей второго порядка, тогда для установления распадения линии их пересечения пользуются следующим положением.
Если две поверхности второго порядка описаны около третьей поверхности второго порядка (или вписаны в нее), то линия их пересечения распадается на две плоские кривые второго порядка.
Это положение, известное как теорема Монжа, является следствием из положения о двойном прикосновении. Покажем это на следующем примере.
Рис. 157
Пример 5. Построить линию пересечения конической и цилиндрической поверхностей, описанных около одной и той же сферы (рис. 158).
Линией прикосновения конической поверхности и сферы будет окружность 1–2, а цилиндрической поверхности и сферы – окружность 3–4. Точки М и N пересечения этих окружностей и будут точками двойного прикосновения конической и цилиндрической поверхностей, так как в этих точках у этих поверхностей будет общая касательная плоскость. Таким образом, имеем двойное прикосновение данных поверхностей и, следовательно, линия их пересечения распадается на пару плоских кривых второго порядка. В рассматриваемом примере линия пересечения распадается на пару эллипсов АВ и CD, которые на виде спереди изображаются отрезками прямых АВ и СD.
4. В заключение рассмотрим применение теоремы Монжа при конструировании трубопроводов, выполняемых из листового материала.
Пример 6. Построить переходные конические поверхности, соединяющие данные цилиндрические трубы I, II и III, оси которых находятся в одной фронтальной плоскости (рис. 159).
Рис. 158
Если вписать в каждую из данных труб сферу, то каждая пара сфер, вписанных в трубы I, II и I, III, определит переходные конические поверхности IV и V, касательные к этим сферам. При построении линий пересечения данных и переходных поверхностей следует учесть теорему Монжа, из которой следует, что искомые линии пересечения будут плоскими кривыми (эллипсами). На виде спереди эти линии будут отрезками прямых АС, ВС, СD, EF и GН, определяемыми точками пересечения очерковых образующих.
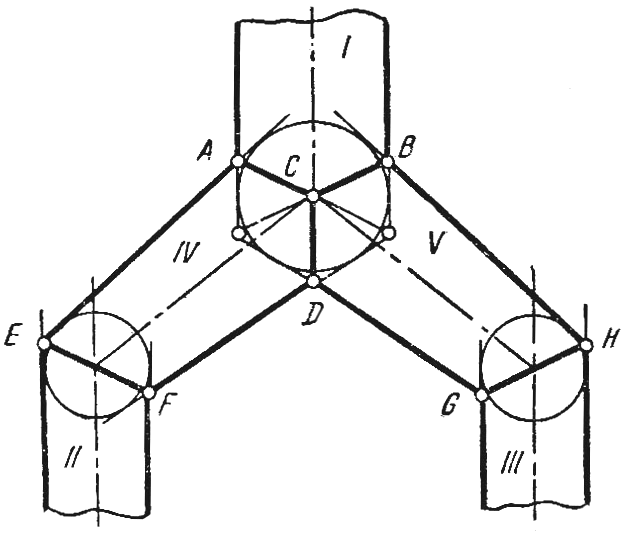
Рис. 159