§ 5. Плоскости, касательные к поверхностям

1. Если на какой-нибудь кривой поверхности Д (рис. 130) провести через ее обыкновенную точку М произвольные кривые линии а, b, c, … и к этим кривым в точке М построить касательные прямые t¹, t², t³..., то все касательные прямые будут лежать в одной плоскости Б, называемой касательной плоскостью к поверхности^.

Рис. 130

Таким образом, касательная плоскость является геометрическим местом всех касательных, проведенных к данной кривой поверхности, проходящих через одну ее точку. Очевидно, что для построения касательной плоскости к поверхности в ее точке М достаточно через эту точку провести на поверхности только две кривые линии а и b и к ним построить касательные прямые t¹ и t². Эти две касательные прямые и определят касательную плоскость Б. Разумеется, что в качестве таких двух кривых линий поверхности следует выбирать ее простейшие линии. Так, в случае линейчатой поверхности одной из этих кривых может служить ее прямолинейная образующая (она совпадает со своей касательной), а в случае поверхности вращения – ее параллель. В зависимости от вида поверхности касательная плоскость может иметь с поверхностью только одну общую точку, например, в случае сферы (рис. 131), или бесчисленное множество общих точек, составляющих прямую или кривую линии, например, в случае конической поверхности (рис. 132) или поверхности кольца (рис. 133).

В приведенных выше случаях поверхность располагается по одну сторону от касательной плоскости, которая не пересекает поверхности. Однако касательная плоскость может и пересекать поверхность по какой-нибудь линии. Так, например, в случае однополостного гиперболоида касательная плоскость пересекает его по двум образующим а и b, которые вместе с тем будут и касательными t¹ и t², определяющими касательную плоскость Б (рис. 134).

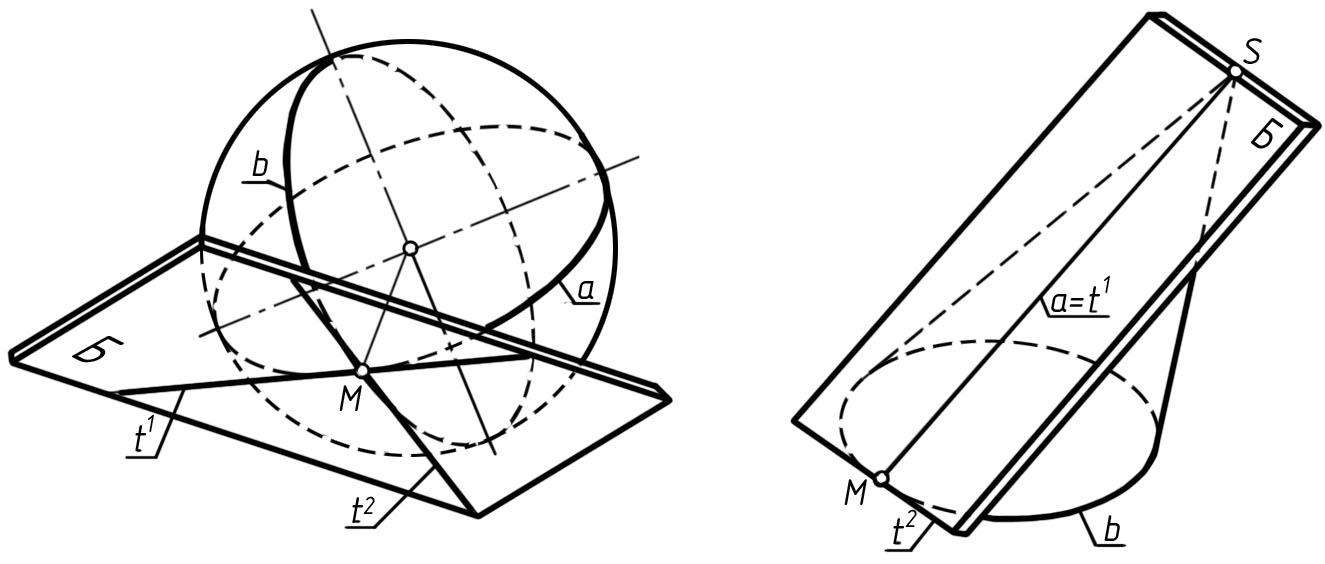
Рис. 131 Рис. 132

Рис. 133

2. Рассмотрим несколько примеров построения касательной плоскости к различным поверхностям.

Пример 1. Построить плоскость Б, касательную к поверхности вращения в ее точке М (рис. 135).

В качестве двух кривых линий поверхности вращения, касательные к которым определяют искомую плоскость Б, выберем параллель h и меридиан а данной поверхности, проходящие через точку М. Так как параллель h является окружностью, расположенной горизонтально, то построение касательной t¹ не вызывает затруднений. Для построения же касательной t² к меридиану а предварительно поворачиваем его вокруг оси поверхности вращения до фронтального положения . При этом данная точка М займет положение .Если теперь построить касательную к фронтальному меридиану в его точке ,то, произведя обратное вращение, получим искомую касательную t² к меридиану а.

Рис. 134 Рис. 135

Таким образом, касательная плоскость Б определена двумя пересекающимися прямыми t¹ и t².

Пример 2. Построить плоскость Б, касательную к конической поверхности в ее точке М (рис. 136).

Так как данная поверхность линейчатая, то, проведя через данную точку М образующую l, являющуюся в то же время и своей касательной, получим одну из прямых, определяющих искомую плоскость Б. Второй прямой, определяющей плоскость Б, будет касательная t к окружности h в ее точке М, проведенной на конической поверхности.

Касательная t параллельна касательной t¹, проведенной в точке N к окружности h¹ основания конической поверхности. Поэтому искомую касательную плоскость Б можно определить образующей l и касательной t¹ к окружности h¹ основания конической поверхности, не строя вспомогательной окружности h, проходящей через данную точку М.

Необходимо заметить, что касательная плоскость к конической или цилиндрической поверхности и вообще ко всякой поверхности торса касается поверхности по всей образующей.

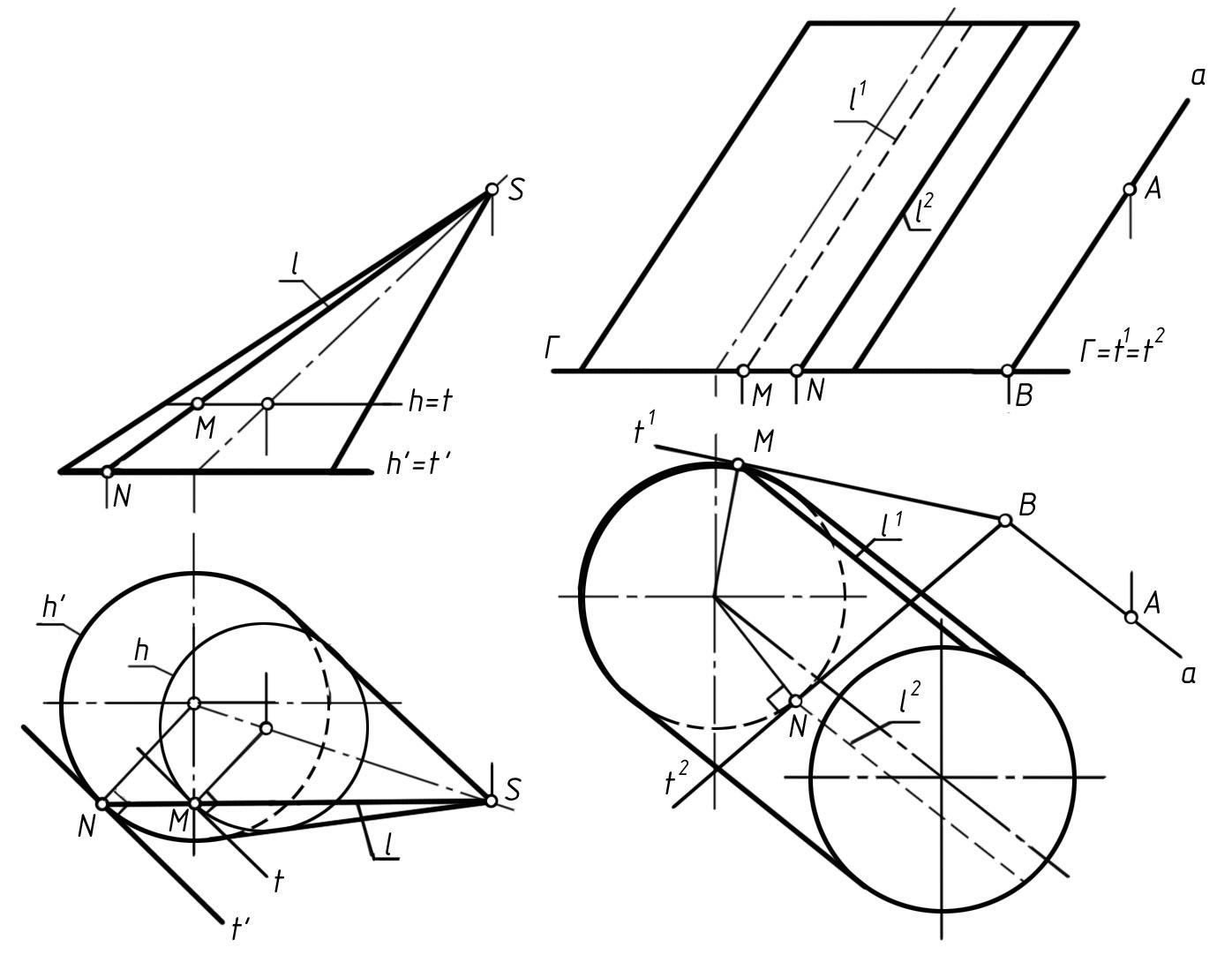
Рис. 136 Рис. 137

Пример 3. Построить плоскость Б, касательную к цилиндрической поверхности и проходящую через точку А, заданную вне цилиндрической поверхности (рис. 137).

Так как искомая касательная плоскость должна содержать в себе образующую цилиндрической поверхности, то в этой плоскости можно провести через данную точку А прямую а, параллельную образующим цилиндрической поверхности.

Если теперь провести через точку В – пересечения прямой а с плоскостью Г – касательные прямые t¹ и t² к окружности основания цилиндрической поверхности, то прямая а и касательные t¹ и t² определят две искомые касательные плоскости Б¹ (a ∩ t¹) и Б² (a ∩ t²). Эти плоскости касаются цилиндрической поверхности по ее образующим l¹ и l².

Кроме указанных выше случаев задания касательной плоскости, ее можно задавать и другими условиями, характер которых зависит от вида поверхности.

Так, к сфере можно проводить касательную плоскость, ставя условие, чтобы она проходила через заданную прямую, не пересекающую сферу и была параллельна некоторой заданной плоскости и т. д.

К конусу касательную плоскость можно проводить так, чтобы она проходила через точку, расположенную вне поверхности конуса и была параллельна некоторой прямой и т. д.