
getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie / getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie
.pdf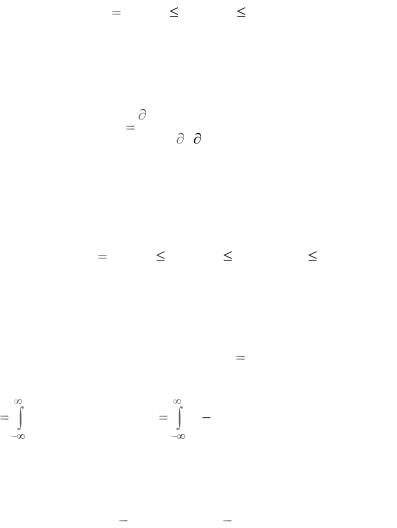
Общий |
вид |
функции плотности |
распределения |
вероятностей |
|
р1(yi , ti ) |
представлен на рис. 3.1.1б. |
|
|||
Функция |
двумерного закона |
распределения |
вероятностей |
||
F2 (yi , ti , |
y j , t j ) определяется |
как |
вероятность одновременного |
||
выполнения двух неравенств |
|
|
|
||
|
|
F2 (yi , ti , y j , t j ) |
P{Y(ti ) yi , Y(t j ) y j}. |
||
В том случае, если функция F2 (yi , |
ti , y j , t j ) дифференцируема по |
||||
уi , y j , то вводится функция двумерной плотности распределения
вероятностей p2 (yi , |
ti , |
y j , |
t j ) на основе частных производных |
||||||||||
|
|
|
|
|
|
|
2F (y , t , y |
j |
, t |
j |
) |
|
|
p (y , t , y |
|
, t |
|
) |
2 i |
i |
|
|
. |
||||
j |
j |
|
|
|
|
|
|
||||||
2 i |
i |
|
|
|
yi |
y j |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
Функция n-мерного закона распределения вероятностей для случайного сигнала определяется на основе обобщения одномерного и двумерного законов и вычисляется как вероятность одновременного выполнения системы из n неравенств для моментов вре-
мени t1, t2 ,...,tn :
Fn (y1, t1, y2, t2,..., yn, tn ) P{Y(t1) y1, Y(t2 ) y2,..., Y(tn ) yn}.
Рассмотрим моментные характеристики первого порядка для одномерных функций плотности распределения вероятностей слу-
чайного сигнала. Математическим ожиданием и дисперсией слу-
чайного сигнала Y(t) называются неслучайные функции my (t),
Dy (t), которые при каждом значении времени t |
ti равны матема- |
|||
тическому ожиданию и дисперсии случайной величины Y(ti ) : |
||||
m (t ) |
yp (y , t )dy , |
D (t ) |
(y m )2 p (y , t )dy . |
|
y i |
1 i i i |
y i |
y |
1 i i i |
Корреляционной (автокорреляционной) функцией случайного сиг-
нала Y(t) называется функция |
Ryy (ti , t j ), значения которой для |
|
моментов времени ti , t j |
равны корреляции для центрированных |
|
случайных величин |
Y(ti ) |
my (ti ), Y(t j ) my (t j ). Функция |
|
|
81 |

Ryy (ti , t j ) является неслучайной и определяется на основе функции двумерной плотности распределения вероятностей:
Ryy (ti , t j ) (yi my (ti ))(y j my (t j )) p2 (yi , ti , y j , t j ) dyi dy j .
Очевидно, в соответствии с определением, корреляционная функция не изменится, если к рассматриваемому случайному сигналу добавить произвольную детерминированную функцию. Если берутся два случайных сигнала X(t), Y(t), то для них определяется
взаимная корреляционная функция, которая принимает вид
Rxy (ti , t j ) (xi mx (ti ))(y j my (t j )) p2 (xi , ti , y j , t j ) dxi dy j .
Введѐнные моментные характеристики имеют вполне нагляд-
ный физический смысл: my (t) определяет функцию времени для среднего значения случайного сигнала, Dy (t) представляет собой
функцию времени для среднеквадратичного отклонения случайного сигнала от среднего значения. Функция двух временных переменных Ryy (ti , t j ) определяет усреднѐнное произведение центрирован-
ных значений сигнала для разнесѐнных моментов времени ti , t j .
3.1.2.Оценивание статистических характеристик сигналов на множестве реализаций
Рассмотрим получение для случайных сигналов оценок функций плотностей распределения вероятностей и моментных характеристик на множестве реализаций. Пусть yn (t) – реализации слу-
чайного сигнала Y(t), n 1,..., M, M – число реализаций сигнала. Будем полагать, что для некоторого момента ti имеются M значений наблюдений yn (ti ).
Для вычисления оценки функции одномерной плотности распределения вероятностей в виде гистограммы найдѐм макси-
мальное ymax |
и минимальное ymin значения наблюдения сигнала |
для ti : ymin |
yn (ti ) ymax , n 1,..., M. Разобьѐм интервал (ymin, |
|
82 |
ymax) |
на |
k |
интервалов |
выбранными |
точками |
y1, y2,..., yk |
1, |
||||
ymin |
y1 |
y2,..., yk 1 |
ymax |
(ymin |
y0 , ymax |
yk ). |
|
|
|||
Определим |
индикаторную |
функцию: I(x) 1, |
x 0, I(x) |
0, |
|||||||
x 0. Для интервала (ts 1, ts ) , |
s |
1,..., k, |
подсчитаем Ms (ti ) число |
||||||||
выполнений неравенства ts |
1 |
yn (ti ) ts : |
|
|
|
|
|||||
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
Ms (ti ) |
I(yn (ti ) ys 1) I(ys |
yn (ti )). |
|
||||||
|
|
|
|
n 1 |
|
|
|
|
|
|
|
Оценка плотности вероятности случайного сигнала для момента времени ti на интервале с номером s вычисляется в виде кусочнопостоянной функции как отношение
p |
(y , t ) |
Ms (ti ) |
, |
y |
y y ; |
p |
(y , t ) 0, |
y y |
, y y . |
|||
|
||||||||||||
1s |
i i |
M |
s 1 |
i |
s |
1s |
i i |
i |
s 1 |
i |
s |
|
|
|
|
|
|
|
|
|
|
|
|
||
Для всего интервала ymin |
y(ti ) |
|
ymax оценка функции плотности |
|||||||||
распределения вероятностей представится системой кусочнопостоянных функций
|
k |
p1 (yi ,ti ) |
p1s (yi ,ti ). |
|
s 1 |
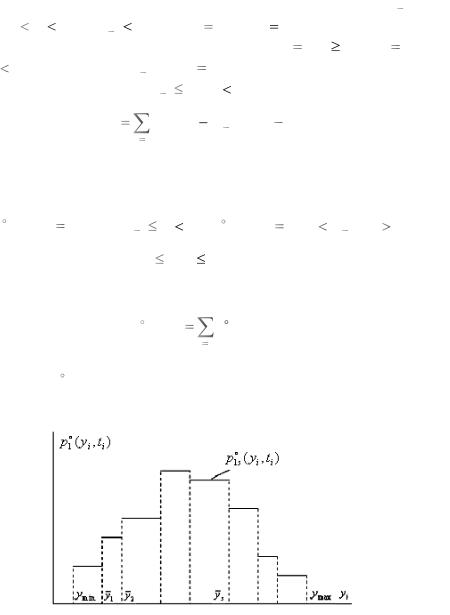
На рис. 3.1.2 схематически |
изображена кусочно-постоянная |
функция p1 (yi , ti ) оценки одномерной плотности распределения вероятностей, полученная в форме гистограммы.
Рис. 3.1.2. Функция оценки одномерной плотности распределения вероятностей
83

Оценки моментных характеристик случайных сигналов для вре-
мени ti (ti , |
t j ) на множестве реализаций вычисляются по следую- |
||||||||||
щим формулам: |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
m |
|
|
1 |
M |
|
|
|
m (t ) |
|
|
|
y (t ), D (t ) |
|
(y (t ) m (t ))2 |
, |
||||
|
|
|
|||||||||
y |
i |
|
|
|
n i |
|
y i |
|
n i |
y i |
|
|
|
M n 1 |
|
|
M 1n 1 |
|
|
||||
|
|
|
|
1 |
M |
|
|
|
|
|
|
R |
(t ,t ) |
|
(y (t ) |
m (t ))(y (t ) |
my (t j )). |
|
|||||
|
|
|
|
||||||||
yy i j |
|
M 1n 1 |
n i |
y i |
n j |
|
|||||
|
|
|
|
|
|
|
|
|
|
||
3.1.3. Стационарные сигналы, оценивание статистических характеристик для стационарных сигналов
Стационарность случайных cигналов подразумевает неизменность их статистических характеристик во времени.
Случайный сигнал называется стационарным в узком смысле, если его n-мерные функции закона распределения вероятностей для группы переменных у1,..., уn , сдвинутых на время , совпада-
ют и, таким образом, не зависят от времени сдвига
Fn (y1, t1 , y2, t2 ,..., yn, tn ) Fn (y1, t1, y2, t2,..., yn , tn ).
Случайный сигнал является стационарным в широком смысле,
если его математическое ожидание и дисперсия не зависят от вре-
мени – my (t) my , Dy (t) |
Dy , а его корреляционная (ковариаци- |
|
онная) |
функция зависит |
от разности аргументов – Ryy (ti , t j ) |
Ryy (ti |
t j ) Ryy ( ), ti t j . |
|
Стационарный сигнал является эргодическим, если нахождение его статистических характеристик может быть осуществлено усреднением по одной реализации y(t) с помощью интегрирования
на конечном временном интервале длительностью T0 с последующим предельным переходом T0 :
|
|
1 |
T0 |
|
my (T0 ) |
|
|
y(t)dt, |
|
|
T0 |
|||
|
|
|
0 |
|
|
1 |
T0 |
|
|
D (T ) |
|
|
(y(t) m )2 |
|
|
|
|||
y 0 |
T0 0 |
y |
||
|
|
|||
|
|
|
|
84 |
lim my (T0 ) my ,
T0
dt, lim Dy (T0 ) Dy ,
T0
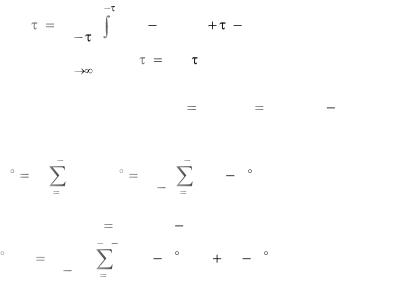
|
|
1 |
T0 |
Ryy (T0, ) |
|
(y(t) my )(y(t ) my )dt, |
|
T0 |
|
||
|
|
0 |
|
|
|
|
lim Ryy (T0 , ) Ryy ( ).
T0
При дискретизации единственной реализации случайного стационарного эргодического сигнала y(i) y(Ti), i 0, 1,..., N 1,
N – число наблюдений сигнала, возможна запись оценок математического ожидания и дисперсии в следующем виде:
|
1 |
N 1 |
1 |
|
N 1 |
m |
|
y(i), D |
|
|
(y(i) m )2. |
|
|
|
|||
y |
|
y |
|
|
y |
|
N i 0 |
N |
1 i 0 |
||
Оценка корреляционной функции представится как функция
дискретного аргумента m, |
m |
0, 1,..., N 1: |
||
|
1 |
|
N m 1 |
|
Ryy (m) |
|
|
(y(i) my )(y(i m) my ). |
|
N m |
|
|||
|
i |
0 |
||
3.1.4.Нестационарные сигналы, оценивание локальных статистических характеристик для нестационарных сигналов
К нестационарным сигналам относятся все случайные сигналы, не удовлетворяющие сформулированным ранее условиям стацио-
нарности. Параметры или статистические характеристики нестационарных сигналов зависят от времени и в общем случае могут быть установлены усреднением на множестве реализаций. Однако во многих инженерных приложениях для анализа сигналов на стационарность, как правило, не бывает достаточного количества реализаций (чаще всего в распоряжении бывает только одна реализация), и это обстоятельство затрудняет проведение статистического оценивания.
Один из подходов к исследованию статистических характеристик нестационарных сигналов состоит в реализации разбиения основного временного интервала наблюдения сигнала на некоторое количество локальных (малых) временных интервалов, на которых рассматриваемый нестационарный сигнал допустимо считать квазистационарным (почти стационарным), и проведения соответствующего статистического анализа на образованной последовательности локальных интервалов, с последующим объединением
85

набора локальных оценок для получения нестационарных статистических характеристик сигнала в целом. На локальных интервалах более удобно осуществлять определение статистических характеристик, которые в этом случае являются локальными и оцениваются на основе построения упрощѐнных локальных моделей сигналов.
Пусть наблюдается в общем случае нестационарный случайный сигнал y(i), i 0, 1,..., N f 1, N f – общее число наблюдений.
Ставится задача получения функций оценок математических ожиданий и дисперсий для нестационарного сигнала по одной реализации. Общий интервал времени наблюдения разбивается на m локальных интервалов, j – номер локального интервала, j 1, 2,..., m, через N1, N2,..., Nm 1 обозначаются номера точек,
где происходит стыковка локальных интервалов. К локальному интервалу с номером j принадлежат точки с номерами, которые удовлетворяют неравенствам: N j 1 i N j , N0 0, N0 N f .
В пределах выделенных локальных интервалов будем считать, что случайные сигналы являются квазистационарными. Тогда последовательность для локальных оценок математических ожиданий и дисперсий исследуемого сигнала на локальных интервалах вычисляется следующими суммами:
|
1 |
N j |
1 |
1 |
N j 1 |
|
|
|
|
m |
|
y(i), D |
|
|
(y(i) m |
)2, |
j 1, 2,..., m. |
||
|
|
|
|
|
|||||
y, j |
N i N |
y, j |
N 1i N |
|
y, j |
|
|
||
|
j 1 |
j 1 |
|
|
|
||||
|
|
|
|
|
|
|
|
||
Оценки указанных статистических характеристик нестационарного сигнала на основном временном интервале будут представляться в виде кусочно-постоянных функций.
3.2.Оценивание и устранение трендов для нестационарных сигналов
3.2.1. Определение трендовых функций для нестационарных сигналов
В ряде случаев нестационарные сигналы могут обладать особенностями, которые значительно упрощают задачи цифровой обработки. Вполне возможны ситуации, когда исследуемые случайные нестационарные сигналы имеют специальную структуру, позво-
86
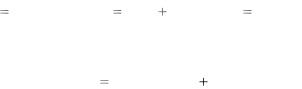
ляющую выделить в них детерминированные низкочастотные трендовые функции.
Положим, что рассматриваемые нестационарные сигналы описываются функциональными моделями, которые специальным образом учитывают их нестационарный характер. Пусть является заданным исходный стационарный широкополосный сигнал х0 (t) с
нулевым математическим ожиданием и единичной дисперсией и составляющие модулирующие функции р1(t), р2 (t), р3(t). На их
основе определяются нестационарные сигналы х1(t), х2 (t), х3(t) с
модулирующими функциями, которые действуют мультипликативно, аддитивно или изменяют временной масштаб:
х1(t) р1(t)х0 (t), х2 (t) х0 (t) р2 (t), х3(t) х0 (tр3(t)). (3.2.1)
Возможны определения нестационарных сигналов вида х4 (t) с действием комбинаций модулирующих функций, например, в виде
х4 (t) р1(t)х0 (tр3(t)) р2 (t). |
(3.2.2) |
Формулы для функциональных моделей сигналов (3.2.1), (3.2.2) допускают различные варианты обобщений; так, в ряде случаев нестационарные сигналы могут состоять из суммы нескольких модулированных несущих сигналов или быть многомерными.
Модулирующие функции р1(t), р2 (t), р3(t) обусловливают нестационарный характер сигналов х1(t), х2 (t), х3(t) и х4 (t). Как правило, функции р1(t), р2 (t), р3(t) являются низкочастотными; по отношению к этим функциям сигнал х0 (t) имеет существенно более высокие частоты. Условие низкочастотности для функций р1(t), р2 (t), р3(t) почти эквивалентно введению ограничений на
их производные; поэтому в ряде случаев используется термин «медленные» модулирующие функции. Иногда модулирующие функции р1(t), р2 (t) называются трендовыми.
3.2.2.Алгоритмы локального оценивания трендовых функций, устранение трендовых функций
В практике ЦОС существует целое множество задач, в которых требуется произвести оценивание указанных трендовых функций
87

для нестационарных сигналов или осуществить их устранение (центрирование и нормализацию).
Перейдѐм от непрерывных функций в (3.2.1), (3.2.2) к дискретным x(Ti), x0 (Ti), p1(Ti), p2 (Ti). Будем рассматривать на-
блюдения нестационарных сигналов, описываемых функциональными моделями типа (3.2.1), (3.2.2), y(Ti), i 0, 1,..., N f 1. Осу-
ществим разбиение временного интервала наблюдения на m рав-
ных локальных интервалов по N точек, допустим, что mN |
N f . К |
||
локальному интервалу с номером j, |
j 1,..., m, принадлежат точки |
||
с |
номерами, которые удовлетворяют неравенствам N( j 1) |
||
i |
Nj 1 . Пусть модельные наблюдения формируются с помо- |
||
щью соотношения |
|
|
|
|
y(Ti) x(Ti) |
w(Ti), |
(3.2.3) |
где w(Ti) – модельные помехи, являющиеся случайными независимыми нормальными числами с нулевым математическим ожида-
нием и дисперсией |
2 . |
|
w |
Рассмотрим нестационарный случайный сигнал с мультипликативным и аддитивным трендами вида
(3.2.4)
Будем полагать, что трендовые функции р1(Ti), р2 (Ti) , яв-
ляющиеся медленными, могут быть заменены на локальных интервалах на кусочно-постоянные. Примем, что мультипликативная трендовая функция всегда положительна p1(Ti) p0 0; в этом
случае оценки трендовых функций p1 j (Ti), p2 j (Ti) на локальных
интервалах совпадают с оценками математических ожиданий и дисперсий:
|
|
1 |
|
Nj 1 |
|
|
|
|
|
|
|
1 |
Nj 1 |
|
|
|
m |
|
|
|
y(Ti), D |
|
|
|
|
(y(Ti) m |
)2, |
||||||
j |
|
|
|
j |
|
|
|
|
||||||||
|
N i N( j 1) |
|
|
|
|
|
N 1i N( j 1) |
|
j |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2 |
Dj , |
j |
1,..., m, |
|
|
(3.2.5) |
|||||
|
|
|
|
|
j |
|
|
|
||||||||
p1 j (Ti) |
j , |
p2 j (Ti) |
|
mj |
для N( j |
1) i |
Nj |
1, |
||||||||
p1j (Ti) 0, p2 j (Ti) |
0 |
для |
0 |
i |
N( j 1), |
N( j |
1) i |
N f 1. |
||||||||
|
|
|
|
|
|
|
|
|
|
88 |
|
|
|
|
|
|
Оценки трендовых функций представятся в виде суммы оценок на локальных интервалах
m |
|
m |
p1 (Ti) |
p1 j (Ti), p2 (Ti) |
p2 j (Ti), i 0, 1,..., N f 1. |
j 1 |
|
j 1 |
Проиллюстрируем предложенный алгоритм вычислениями на математических моделях. Сигнал x0 (Ti) сформируем с использованием датчика нормальных случайных чисел с нулевым математическим ожиданием и единичной дисперсией; возьмѐм N f 512,
T 0,02 c. Модели для трендовых функций примем в виде
р (Ti) |
p e Ti , |
р (Ti) |
p cos(2 f Ti ), |
1 |
01 |
2 |
02 |
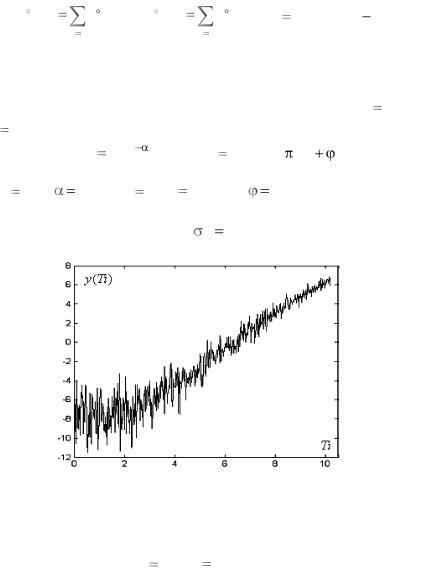
где параметры этих функций принимают следующие значения: р01 2,7, 0,2, р02 8, f 0,04 Гц, 3,1. На рис. 3.2.1 изо-
бражена отдельная реализация модельных наблюдений нестацио-
нарного сигнала (3.2.3), (3.2.4) с |
2 |
0. |
|
w |
|||
|
|
Рис. 3.2.1. Реализация модельных наблюдений нестационарного сигнала
Рис. 3.2.2а и 3.2.2б содержат изображения оценок трендов в виде кусочно-постоянных функций – линии 1, полученные с помощью (3.2.5). Для вычисления оценок число локальных интервалов было принято равным m 16 (N 32). Одновременно на этих же
рисунках отмечены пунктирными линиями 2 модельные трендовые функции.
89
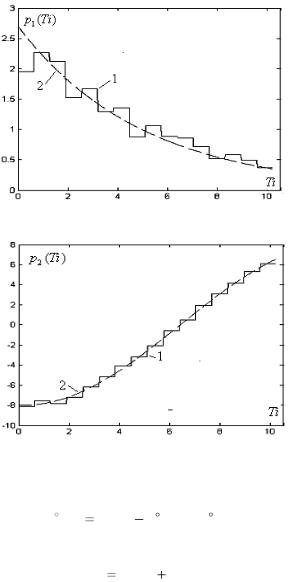
Рис. 3.2.2а. Функция оценки мультипликативного тренда
Рис. 3.2.2б. Функция оценки аддитивного тренда
Устранение трендов в нестационарных сигналах реализуется на основе применения операций центрирования и нормализации:
x (Ti) (y(Ti) p2(Ti)) / p1 (Ti).
Рассмотрим нестационарный случайный сигнал с медленным аддитивным трендом вида
х(Ti) х0 (Ti) р2 (Ti). |
(3.2.6) |
Введѐм локальные интервалы. Будем полагать, что трендовая функция р2 (Ti) может быть с достаточной точностью заменена на
локальных интервалах последовательностью локальных модельных кусочно-линейных функций вида
90
