Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белгородский университет кооперации, экономики и права

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie / getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie

.pdf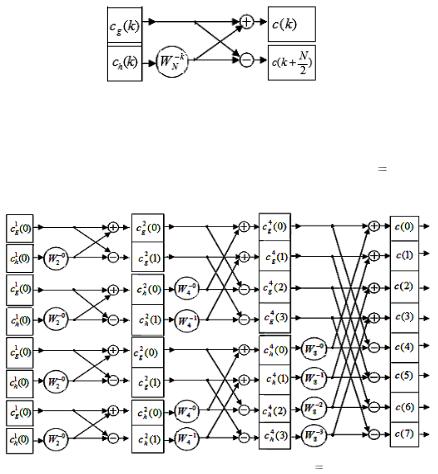

Скачиваний:

Добавлен:

18.03.2016

Размер:

6.41 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 2417 18 19 20 21 22 23 24 > Следующая >>>

Рис. 4.5.1. Граф операции «бабочка»

Комбинации однотипных «бабочек» при вычислении коэффициентов ДПФ составляет основу алгоритма БПФ. На рис. 4.5.2 представлен в качестве примера граф алгоритма БПФ для N 8, состоящий из трѐх шагов.

Рис. 4.5.2. Граф алгоритма БПФ для N 8

Для удобств рассмотрений введены индексы для промежуточных коэффициентов ДПФ сgN/2(k), сhN/2 (k); показатель N/2 опре-

деляет размерности ДПФ, реализуемых на соответствующем шаге работы алгоритма.

Чтобы предлагаемый алгоритм БПФ начал работать, необходима всего лишь предварительная перетасовка входных данных во временной области. Работу алгоритма перетасовки, в соответствии с разработанным графом рис. 4.5.2, удобно анализировать с право-

161

го конца (от конца к началу), что приллюстрировано на диаграмме рис. 4.5.3.

Оценим временные затраты, необходимые для работы алгоритма БПФ. На каждом шаге алгоритма БПФ выполняется N/2 опера-

ций «бабочка»; в каждой «бабочке» реализуется только одно комплексное умножение, поэтому временные затраты на каждом шаге предлагаемого алгоритма приближѐнно составляют величину N/2 ty . Число шагов в алгоритме БПФ уже было подсчитано ра-

нее; поэтому время вычисления N коэффициентов дискретного преобразования Фурье по предлагаемому алгоритму БПФ представится следующей оценкой

TБПФ N /2ty log2 N.

(4.5.3)

Рис. 4.5.3. Перетасовка входных данных для алгоритма БПФ с N 8

Определим возможный выигрыш во времени по предлагаемому алгоритму БПФ по сравнению с вычислением ДПФ на основе фор-

мул (4.5.1) и (4.5.3):

TДПФ	N2ty	2N
			.
ТБПФ	(N / 2)ty log2 N	log2 N	.

Имеем следующие значения введѐнного показателя эффективности:

N 512,	9	113, N 1024,	10	204, N 8192,	13	1203. Из
	9		10		13
			162

полученных оценок выигрышей следует, что алгоритм БПФ радикально уменьшает временные затраты при вычислении ДПФ.

Список вопросов для самопроверки к гл. 4

1.В чѐм состоит формулировка задачи аппроксимации дискретных наблюдений сигналов полигармоническими моделями и каковы особенности еѐ решения?

2.В чѐм состоят особенности задачи аппроксимации дискретных наблюдений сигналов на основе моделей, линейных по части параметров?

3.В чѐм состоит формулировка задачи аппроксимация дискретных наблюдений сигналов на основе дискретного преобразования Фурье для действительного случая?

4.В чѐм состоит формулировка задачи аппроксимация дискретных наблюдений сигналов на основе дискретного преобразования Фурье для комплексного случая?

5.В чѐм состоит алгоритм вычисления дискретного преобразования Фурье для комплексной синусоиды?

6.В чѐм состоит определение для разрешающей способности ДПФ?

7.Какие свойства дискретного преобразования Фурье приведены в разд. 4.2?

8.В чѐм заключается формулировка теоремы Парсеваля для случая непрерывных сигналов?

9.Каким образом реализуется вывод теоремы Парсеваля для случая дискретных сигналов?

10.В чѐм состоит определение для функции спектральной плотности мощности сигналов (СПМ)?

11.Каким образом реализуется вывод оценки функции СПМ для стационарных эргодических дискретных сигналов?

12.Для каких целей применяются временные окна?

13.Каким образом реализуется алгоритм вычисления оценок параметров сигналов на основе функции СПМ?

14.Каким образом определяется функция взаимной спектральной плотности мощности сигналов (ВСПМ)?

15.Каким образом реализуется алгоритм вычисления оценок разностей фаз на основе функции ВСПМ?

163

16.Каким образом реализуется алгоритм вычисления оценок передаточных функций линейных систем на основе функции ВСПМ?

17.Каким образом реализуется алгоритм вычисления оценок функции когерентности на основе функций СПМ и ВСПМ?

18.Каким образом реализуется алгоритм быстрого преобразования Фурье (БПФ)?

Список задач к гл. 4

1. Вычислить коэффициенты ДПФ ck ,

если

y(i), i

0, 1,..., N

N 1

y(i)W ki ,

0, 1,..., N

N i 0

для заданных временных дискретных последовательностей:

y(i)

Ae j(2 f0Ti

) ; y

0, 1,..., N

y(i)

Acos(2 f0Ti

);

0, 1,...,

0, 1,..., N

y(i)

Asin(2 f0Ti

);

0, 1,...,

0, 1,..., N

y(i)

0,..., N0

0, 1,..., N

0, i

N0,..., N

y(i)

1, i

i0;

1, k

0, 1,..., N

0,..., i

1, i

1,..., N

y(i)

N1,..., N2

0, 1,..., N

0,..., N1

N2,..., N 1,

y(i)

Ti ;

0, 1,...,

0, 1,..., N

y(i)

Ti ;

cos(2

fTi

); i

0, 1,..., N 1; k 0, 1,..., N 1;

9. y(i)

10)y(i)

11)y(i)

12)y(i)

13)y(i),

Asin(2 f0Ti

), i

0,..., N0

0, 1,..., N

N0 ,..., N

Asin(2 f0Ti), i

N1,..., N2 1;

k 0, 1,..., N 1;

0,..., N

N ,..., N

Ti;

0, 1,..., N

x(i)

z(i); k

0, 1,..., N

1, y(i)

y(i

i0 ),

0, 1,..., N

164

14) y(i),

0, 1,...,

y(i)

y(i)e

) ,

k 0, 1,..., N

15) y(i)

x(i)z(i), k

0, 1,..., N

Определить характеристики разрешения составляющих двух-

частотного сигнала на основе ДПФ

y(Ti)

A cos2 f Ti

A cos2

f Ti,

0, 1,..., N

Разрешимы ли составляющие сигнала с параметрами: A1

1,0;

1,5; f1

5 Гц; f2

5,5 Гц; T

0,01 c;

512?

Разрешимы ли составляющие сигнала с параметрами: A1

1,0;

1,5; f1

5 Гц; f2

10,5 Гц; T

0,01 c;

512?

Для

параметров

сигнала:

1,0;

1,5;

5 Гц;

5,5 Гц;

0,01 c, какое необходимо задать N для обеспече-

ния разрешения составляющих?

Для

параметров

сигнала:

1,0; A

1,5;

5 Гц,

5,5 Гц, какой необходимо задать интервал наблюдения NT для

обеспечения разрешения составляющих?

Для параметров cигнала:

1,0;

1,5;

f 5 Гц и ин-

тервала наблюдения NT 4 c, какое минимальное значение частоты f2 может обеспечить разрешение составляющих?

165

Глава 5. ДИСКРЕТНЫЕ СВЁРТКИ

5.1. Определения дискретных свёрток

Дискретные свѐртки достаточно часто встречаются в различных задачах ЦОС, например при вычислении выходных сигналов линейных динамических систем. Приведѐм определения для дискретных свѐрток, основываясь на предварительных сведениях, помещѐнных в разд. 1.2.2.

Пусть заданы две последовательности h(i), y(i), определѐнные в дискретных точках. Первая последовательность h(i) служит ядром свѐртки, вторая последовательность y(i) представляет собой дис-

кретные значения входного сигнала. Будем полагать, что дискретные индексы для указанных последовательностей могут принимать значения в заданных диапазонах. Этим двум последовательностям ставится в соответствие выходная дискретная последовательность x(i). Устанавливаются нижние и верхние пределы суммирования в

свѐртках S1, S2 и пределы изменения индексов I1, I2 для выход-

ной последовательности. Дискретные свѐртки с постоянными и с переменными пределами суммирования представляются формулами

	S2	S2 (i)
x(i)	h(i s) y(s), x(i)	h(i s)y(s), I1 i I2. (5.1.1)
s	S1	s S1(i)

Свѐртка двух бесконечных последовательностей h(i), y(i) определяется следующим образом:

x(i)

h(i s)y(s),

(5.1.2)

Свѐртки типа (5.1.2) называются линейными, их не следует путать с круговыми свѐртками для периодических последовательностей, которые будут рассматриваться позже.

Целесообразно отметить существенное обстоятельство для свѐрток – различное направление изменения (с разными знаками) индексов сомножителей при суммировании. Задачи, которые воз-

никают при нахождении дискретных свѐрток, состоят, в основном,

166

в эффективном вычислении по точности и быстродействию выходной последовательности x(i) для заданных дискретных последова-

тельностей h(i), y(i) с учѐтом их особенностей.

5.2. Вычисление прямых и обратных круговых свёрток

Перейдѐм к определению круговых свѐрток (прямых круговых свѐрток). Пусть заданы дискретные периодические с периодом N последовательности h(i), x(i), i , h(i) h(i N),

y(i) y(i N). По определению дискретная круговая свѐртка представляется выражением

N 1

x(i) h(i s)y(s), i 0, 1,..., N 1. (5.2.1)

s 0

Процедуру вычисления круговой свѐртки удобно наглядно представить на круговых диаграммах, изображѐнных на рис. 5.2.1а, 5.2.1б в виде систем из внутренней и внешней окружностей, которые могут пошагово вращаться друг относительно друга.

Рис. 5.2.1а. Процедура вычисления		Рис. 5.2.1б. Процедура вычисления
круговой свѐртки для i = 0, N = 12		круговой свѐртки для i = 1, N = 12
Значения	для периодического	входного сигнала y(s),
s 0, 1,..., N	1, располагаются на внутренней окружности данной

круговой диаграммы, значения для периодического ядра – на внешней окружности. Нахождение свѐртки x(i), i 0, 1,..., N 1, сводится к пошаговому вращению внешней окружности с после-

167

дующим попарным умножением и суммированием. На рис. 5.2.1а, 5.2.1б проиллюстрировано вычисление x(0), x(1):

N 1				N 1
x(0)	h(0	s)y(s),	x(1)	h(1 s)y(s).
s	0			s 0
Сделаем в свѐртке (5.2.1) замену переменных: i					s	m. Из ра-
венства s 0 получаем m		i; из s	N	1 следует	m	i (N 1).

Тогда на основе изменения пределов суммирования записывается равенство для новой круговой свѐртки:

i (N 1)

x(i) h(m)y(i m), i 0, 1,.., N 1.

m i

Проанализировав вычисления на представленной круговой диаграмме, нетрудно заметить, что результат суммирования не изменится, если произвольно изменить точку начала и направление суммирования на круговой диаграмме. Справедливо равенство

	N 1
x(i)	h(m)y(i m).	(5.2.2)
	m 0

Круговую свѐртку в ряде случаев удобно представлять с по-

мощью введения векторно-матричных переменных:
				x(0)			y(0)
				x(0)			y(0)
		x		x(1)		, y	y(1)	,
		x				, y		,
				x(N 1)			y(N 1)
	h(0),			h(	1),		h(	(N	1))
	h(0),			h(	1),		h(	(N	1))
H	h(1	0),		h(1	1),		h(1	(N	1))	, (5.2.3)
H										, (5.2.3)
	h((N	1)	0)				h((N	1)	(N 1))

где выходные и входные векторы x, y имеют размерность (N, 1), матрица свѐртки H имеет размерность (N, N). Результат свѐртки с

использованием (5.2.3) записывается в виде векторно-матричного произведения x Hy.

Очевидно, что временные затраты на нахождение свѐртки, если следовать в вычислениях непосредственно определению (5.2.2),

168

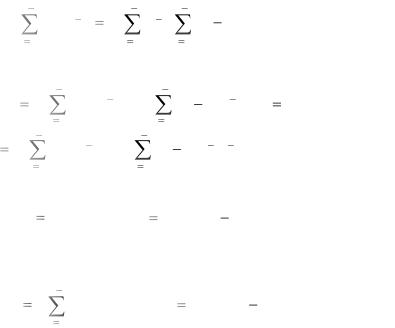
(5.2.3), сравнимы с временными затратами на нахождение ДПФ по прямым формулам.

Рассмотрим алгоритм вычисления круговых свѐрток, позволяющий существенным образом уменьшить временные затраты. Возьмѐм выражение для круговой свѐртки (5.2.1), найдем ДПФ от его левой и правой части:

1	N 1	1	N 1	N 1
	x(i)W ki		W ki	h(i s)y(s).

N i 0		N i 0		s 0

Переставив порядок суммирования, с учѐтом периодичности, получим


с (k)			1	N 1 y(s)W ks N			1	N 1h(i s)W kiW ks
с (k)				N 1 y(s)W ks N				N 1h(i s)W kiW ks
x			N s 0				N i 0
			N s 0				N i 0
	1	N 1 y(s)W ks N			1	N 1h(i s)W k(i s).
		N 1 y(s)W ks N				N 1h(i s)W k(i s).
	N s 0				N i 0

Окончательно запишем выражение в частотной области через произведения ДПФ

cx (k) Ncy (k)ch (k), k 0, 1,..., N 1.

(5.2.4)

Круговые свѐртки могут быть вычислены на основе обратного дискретного преобразования Фурье для произведений ДПФ входной последовательности и дискретной последовательности ядра:

N 1			(k)c (k)W ki , i 0, 1,..., N 1.
x(i) N	c	y	(k)c (k)W ki , i 0, 1,..., N 1.
		y	h
k	0

Временные затраты по предлагаемому методу эквивалентны выполнению трѐх ДПФ и N комплексных умножений. Выигрыш по времени при вычислении круговых свѐрток в частотной области очевиден.

Рассмотрим алгоритм вычисления обратных круговых свѐрток. Нахождение свѐрток, о которых шла речь, обычно интерпретируется как прямая задача, связанная с определением выходной реакции линейной системы с известной импульсной переходной функцией на заданное входное воздействие. Однако возможна другая постановка, имеющая широкие приложения, состоящая в необходимости определения входного воздействия на линейную систему по известной выходной реакции и известной импульсно-переходной функции – эта задача интерпретируется как обратная.

169

Запишем выражение для дискретной круговой свѐртки в скалярном и эквивалентном векторно-матричном виде

		N 1
	x(i)	h(i	s)y(s),		i	0, 1,..., N	1, x	Hy.
		s 0
Нахождение		вектора	входного			воздействия		на	систему
yT	(y(0), y(1),..., y(N		1))	по	известному		выходному		вектору
xT	(x(0), x(1),..., x(N		1))	и квадратной матрице				свѐртки H из

(5.2.3) сводится к решению системы линейных уравнений и записывается в виде y H 1x. Решение подобной задачи во временной

области сопряжено со значительными проблемами – необходимо, чтобы матрица H имела ненулевой определитель – матрица должна быть хорошо обусловленной и размерность этой матрицы должна быть не очень большой, для обеспечения эффективного решения системы линейных уравнений. В большинстве практических задач последнее условие в ряде случаев трудно обеспечить.

Нахождение искомого вектора y, с учѐтом сказанного, удобно производить в частотной области с использованием процедур ДПФ. Воспользуемся сделанной записью свѐртки (5.2.4) на основе ДПФ, выразим ДПФ для искомого входного вектора y через отношение

ДПФ выходного вектора x ДПФ переходной функции – ядра, и далее вычислим обратное ДПФ

(k)

1 cx (k)

, y(i)

N 1

N 1 1

cx (k)

(k)W

N ch (k)

k 0 N ch (k)

k 0

i 0, 1,..., N 1.

Предложенное решение задачи – вычисление обратной свѐртки в частотной области с точки зрения временных затрат, очевидно, значительно эффективнее процедуры решения во временной области.

5.3. Вычисление апериодических свёрток

Рассмотрим алгоритмы вычисления апериодических свѐрток. Пусть последовательности h(i), y(i), входящие в свѐртки (5.1.1),

определены в N1, N2 точках, h(i) 0 для i 0, i N1, y(i) 0 для

170

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 2417 18 19 20 21 22 23 24 > Следующая >>>